一般知識の計算関係まとめ

なるべく暗記量を減らすプロジェクトの一般知識の計算編です．

雲粒の終端速度

速度 $${V}$$ で落下している雲粒にはたらく抵抗力$${F}$$は

$$
F = 6\pi r\eta V
$$

である．ここで大事な変数は雲粒の半径$${r}$$とその速度$${V}$$で，定数は一つにまとめてしまう．

$$
F = KrV  (K\equiv 6\pi\eta)
$$

$${K}$$を使った式さえ覚えておけば終端速度も導出できるようになります．終端速度では，雲粒に係る重力と抵抗力がつり合うから，

$$
mg = KrV \\
\frac{4}{3}\pi r^3\rho_w g = KrV
$$

となる．最後に$${V}$$以外を右側に移動すれば．

$$
V = \frac{4\pi r^2\rho_w g}{3K} = \frac{2\rho_w g}{9\eta}r^2
$$

雲粒の終端速度の導出完了！！

【補足】$${\eta}$$は粘性係数

雨粒の終端速度

速度$${V}$$で落下する雨粒にはたらく抵抗力$${F}$$は

$$
F=\frac{\rho_a V^2 \pi r^2 C_d}{2} = K\pi r^2 C_d V^2  (K\equiv \frac{\rho_a C_d}{2})
$$

である．ここで覚えておくのは抵抗力は雨粒の断面積と落下速度の2乗に比例すること．
雲粒同様に終端速度を求める．

$$
mg = K\pi r^2 C_d V^2 \\
$$

$$
\frac{4}{3}\pi r^3\rho_w g = K\pi r^2 V^2 
$$

$$
V = \Big( \frac{4\rho_g}{3K}r \Big)^{1/2} = \Big( \frac{8\rho_w g}{3\rho_a C_d}r \Big)^{1/2}
$$

終端速度が求められました！

【補足】$${C_d}$$：抵抗係数

凝結過程での降水粒子の成長速度

単位時間当たりの降水粒子の質量の増加量は

$$
\frac{dM}{dt} = r \times \frac{e - e_{max}}{e_{max}} \times 4\pi D\rho_v
$$

である．これは複雑で覚えられそうにない．．．

$$
\frac{dM}{dt} = r\frac{e - e_{max}}{ e_{max}} \times K
$$

を覚えることにする．ここで$${K}$$は

$$
K \equiv 4\pi D\rho_v
$$

と定義した．$${ (e - e_{max})/e_{max} }$$は過飽和度．あとは単位時間あたりの質量の増加量を単位時間当たりの半径の増加量に変換する．$${ M = \frac{4}{3}\pi r^3 \rho_w  }$$を代入して，

$$
\frac{dt}{dt} = \frac{1}{r}\frac{e - e_{max}}{e_{max}} \times \frac{K}{4\pi \rho_w} = \frac{D}{r}\frac{e - e_{max}}{e_{max}}\frac{\rho_v}{\rho_w}
$$

を得る．水滴の半径の増加量は$${r^{-1}}$$に比例する．つまり，ある程度成長した降水粒子は凝結過程ではなかなか成長しないことを示している．

【おまけ】

* $${D}$$：拡散係数
* フックの法則（濃度に差がある場合の溶けている物質の移動速度は濃度勾配に比例）：$${ J = -D\frac{dc}{dx} }$$

併合過程の降水粒子の成長速度

大きい降水粒子と多数の降水粒子が落下しているとする．これらの半径はそれぞれ$${r, r'}$$と表す．単位体積当たりの小さな水滴の量を$${q\rm{[kg/m^3]}}$$とする．降水粒子の単位時間当たりの質量増加量は，大きな降水粒子を水平に2等分する円を底面とし，大きな降水粒子と小さな降水粒子の速度差$${V - V'}$$を高さとする円柱に含まれる小さな降水粒子の質量と等しい．これを式にすると，

$$
\frac{dM}{dt} = \pi r^2(V - V')q
$$

となる．この式は上記の状況をイメージできれば作れる．
$${ V >> V' }$$を仮定すれば，

$$
\frac{dr}{dt} = \frac{Vq}{4\rho_w}
$$

と変形できる！！

1層大気モデルで考える温室効果

図1 1層大気モデル

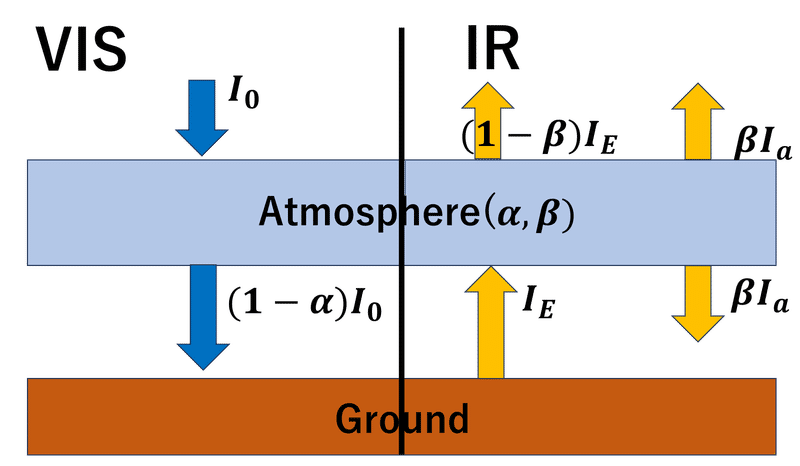
• 可視域，赤外域での大気の吸収率をそれぞれ$${\alpha}$$, $${\beta}$$とする

• キルヒホッフの法則より，赤外域での射出率も$${\beta}$$となる

• $${I_0}$$は太陽放射の強さ[$${\rm{Wm^{-2}}}$$]

• $${I_E, I_a}$$は地表面と大気を黒体としたときの放射強度

予報士試験では$${\alpha=0, \beta=1}$$とすることが多いが，
今回はもう少し複雑な場合を考える．大気，地表面における放射収支は

$$
\alpha I_0 + \beta I_e - 2\beta I_a = 0
$$

$$
(1 - \alpha)I_0 + \beta I_a - I_e = 0
$$

と書ける．
$${I_e, I_a}$$についての連立方程式をみて，これを解く．
解は

$$
I_e = \frac{ 2 - \alpha}{ 2 - \beta} I_0
$$

$$
I_a = \frac{\alpha + \beta - \alpha\beta}{\beta(2 - \beta)}
$$

となる．大気がない場合の地表面の温度を$${T_0}$$として，
シュテファン・ボルツマンの法則を代入すると各温度が$${T_0}$$と$${\alpha, \beta}$$だけで表現できる．

$$
T_e = \Big( \frac{2 - \alpha}{2 - \beta} \Big)^{1/4}T_0
$$

$$
T_a = \Big\{ \frac{\alpha + \beta - \alpha\beta}{\beta(2 - \beta)} \Big\}^{1/4}T_0
$$

例えば，大気が可視域では透明で赤外域では真っ黒のときは，
$${\alpha=0, \beta=1.0}$$，

$$
T_e = 2^{1/4}T_0
$$

$$
T_a = T_0
$$

となる．これは予報士試験でもよく出てくる数値．また，地表面の温度は$${\beta}$$が大きいほど高くなる．これは二酸化炭素の濃度が上がれば，地表面の温度が高くなることを簡単なモデルではあるが定量的に示唆している．

追記

見出し画像の出典は『気候変動監視レポート2012』