Understanding and Solving the Structual Vector Autoregressive Identification Problemの翻訳

2024年4月1日 23:18

これは、Understanding and Solving the Structural Vector Autoregressive Identification Problemの翻訳です。VARの勉強ついでに翻訳したので、公開します。
もし権利上の問題があるようでしたら、すぐに削除します。
翻訳のミスなどがあれば教えてください。

以下　日本語訳

Introduction

構造ベクトル自己回帰モデルは経済的影響や経済的成果を理解したり予想するために用いられる重要な時系列モデルです。ここでは構造ベクトル自己回帰モデルが抱える識別問題とその解決方法について見ていきます。特に以下のことをカバーしています。

構造VARモデルとは何で、誘導形VARとは何か
構造VARと誘導形VARとの関係性は何か
構造VARの識別問題とはなにか
構造VARの識別問題への一般的な解決方法とは何か

構造形VAR VS 誘導形VAR

構造形VAR（以下”SVAR)モデルの制約について理解する最初のステップはSVARと誘導形VARとの違いとつながりを理解することです。

誘導形VARモデルはそれぞれの変数を以下の関数と考えます。

それ自身の過去の値
モデル内の他の変数の過去の値

誘導形VARモデルには以下の特徴があります。

最小二乗法を用いることで簡単に推定することができる
予想に便利である

しかしながら、誘導形VARの大きな問題として、通常はある変数の突然の変化がモデル内の他の変数にどのような影響を与えるかを区別することができないということがあります。

構造形のVARでは

変数間の因果的な関係を調べることができる
VARモデルに構造制約を加えるために経済理論を用いることができる
個々のショックが他の変数に与える影響を調べるのに使用できる。

構造形VARと誘導形VARモデルの関係性

構造VARと誘導形VARモデルの数式を見ていきましょう。$${Y_1,Y_2}$$の２つの内生変数を用いた、２変数のシンプルなモデルを扱います。

$${Y_1,Y_2}$$は以下のようなものであるとしてモデルを組みます。

$${Y_1,Y_2}$$の過去の観測値は一期さかのぼる
$${\epsilon_{1,t},\epsilon_{2,t}}$$はそれぞれの変数のランダムなショックである

数学的にこれらを二つの連立方程式として表せられます。

$${y_{1,t}= \phi_{11}y_{1,t-1}+\phi_{12}y_{2,t-1} + b_{11}\epsilon_{1,t}+b_{12}\epsilon_{2.t}}$$

この構造VARモデルには各変数への$${\epsilon_{1,t},\epsilon_{2,t}}$$の個別のショックが同時ショックを含んでいます。これらのショックは

未観測でゼロ平均のホワイトノイズ過程である
互いに厳密に無相関で、独立である

このモデルでは以下の形で表される行列B

$$
B=\begin{bmatrix} b_{11} & b_{12} \\ b_{21} & b_{22} \end{bmatrix}
$$

がショックである$${\epsilon_{1,t},\epsilon_{2,t}}$$が内生変数$${Y_1,Y_2}$$に与える構造的影響をとらえています。

これは簡単な連立方程式のように見えるかもしれませんが、$${\epsilon_{1,t},\epsilon_{2,t}}$$は観測されておらず、Ｂを推定することはできないということに注意してください。

ここで誘導形VARの出番となります。これ理解するために”ショック”の要素を組み合わせて定義します。

$$
u_{1,t}=b_{11}\epsilon_{1,t} + b_{12}\epsilon_{2,t}\\
u_{2,t} = b_{21}\epsilon_{1,t} + b_{22}\epsilon_{2,t}
$$

ここで、二つの連立方程式は誘導形VARモデルになります。

$$
y_{1,t}= \phi_{11}y_{1,t-1}+\phi_{12}y_{2,t-1} + u_{1,t}\\
y_{1,t}= \phi_{11}y_{1,t-1}+\phi_{12}y_{2,t-1} + u_{2,t}\\
$$

誘導形VARモデルでは、OLSを用いることで、未知のパラメーターを推定することができます。

$$
\phi = \begin{bmatrix}
\phi_{11} & \phi_{12} \\
\phi_{21} & \phi_{22}
\end{bmatrix}
$$

しかしながら、これらの推定からの残差では、ショックの$${\epsilon_{1,t},\epsilon_{2,t}}$$の$${Y_1,Y_2}$$への影響を決定することはできません。

なぜSVAR制約が必要なのか

誘導形のVARから$${Y_1,Y_2}$$ $${Y_{2,t}}$$$${\epsilon_{1,t}}$$と$${\epsilon_{2,t}}$$のショックの影響を逆算するために、以下の関係から始めます。

$$
u_{1,t}=b_{11}\epsilon_{1,t}+b_{12}\epsilon_{2,t}\\
u_{2,t}=b_{21}\epsilon_{1,t}+b_{22}\epsilon_{2,t}
$$

あるいは、線形代数の形を用いて、

$${U_t=B\epsilon_t}$$

この関係から、線形代数といくつかの統計的関係を用いることで、構造VARの関係を実装する際の核となる恒等式を導くことができます。

$$
\Sigma_u = BB'
$$

ここで、$${\Sigma_u}$$は誘導形の残差の共分散行列です。

$$
\Sigma _u = \mathbb E[u'_tu_t]
$$

この問題を理解するために、２変数のモデルでこれらが何を指しているのかをもう一度考えてみましょう。まず、$${\Sigma _u}$$は誘導形のモデルからの残差の共分散行列であることに注意してください。

$$
\Sigma _u = \begin{bmatrix}
\sigma^2_{11} & \sigma_{12}^2 \\
\sigma^2_{21} & \sigma^2_{22}
\end{bmatrix}
$$

これは、$${\Sigma_u = BB'}$$は下の式に等しいことを意味しています。

$$
\begin{bmatrix}
\sigma^2_{11} & \sigma_{12}^2 \\
\sigma^2_{21} & \sigma^2_{22}
\end{bmatrix}=\begin{bmatrix}
b_{11} & b_{12} \\
b_{21} & b_{22}
\end{bmatrix}\begin{bmatrix}
b_{11} & b_{12} \\
b_{21} & b_{22}
\end{bmatrix}
$$

また、以下の方程式に展開することができます。

$$
\sigma^2_{11} = b^2_{11} + b_{12}^2\\
\sigma^2_{12} = b_{11}b_{21} + b_{12}b_{22}\\
\sigma^2_{21} = b_{11}b_{21} + b_{12}b_{22}\\
\sigma^2_{22} = b^2_{21} + b_{22}^2\\
$$

しかし、$${\sigma^2_{12}=\sigma^2_{21}}$$であることに注意してください。これは、３つの方程式を持っているが、４つの未知の変数があり、モデルを識別不能であることを意味しています。これが、構造VARモデルで起こる識別問題となります。

これを解決するた目には、いくつかの方程式が必要です。これらの方程式は制約の形から用いることができます。

制約をどのように選ぶか

識別制約はたくさんの形があります。例えば以下のようなものがあります。

- 短期では影響がないというもの

- 長期では衝撃がないとするもの

- 符号制約

SVARモデルを識別するための選ぶことは難しく思えるかもしれません。しかし、制約を決定する際の指針は常に理論的背景があるべきです。

例えば、実質GDPへの金融政策の影響をモデリングする際には、貨幣中立説の理論からは、金融政策は実質GDPには影響がないことが示されます。

SVAR研究の例

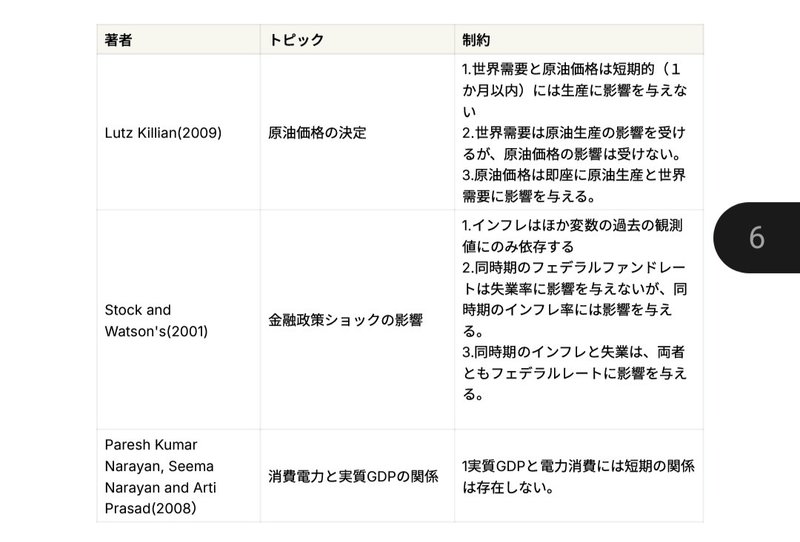
一般的な識別方法

経済理論が頻繁に示す事実を用いることで、識別選ぶことが簡単になります。例えば、以下のものがあります。

短期制約
長期制約
符号制約

短期制約（コレスキー識別）

この識別方法は、あるショックは一つかそれ以上の内生変数には同時点での影響を与えないと仮定します。例えば、金融政策のショックは即座には総需要には影響を与えないと考えられます。

どうやって、短期制約を実装するのか？

以前の２変数の構造VARを思い出してください。

$$
y_{1,t}= \phi_{11}y_{1,t-1}+\phi_{12}y_{2,t-1} + u_{1,t}\\
y_{1,t}= \phi_{11}y_{1,t-1}+\phi_{12}y_{2,t-1} + u_{2,t}\\
$$

$${y_2}$$へのショックは$${y_1}$$には同時点で影響がないと考えると、$${b_{12}=0}$$であると言えます。

また行列$${B}$$は以下のように書けます。

$$
B=\begin{bmatrix} b_{11} &0 \\ b_{21} & b_{22} \end{bmatrix}
$$

行列$${B}$$が下三角になるように変数を並べることができることに注意してください。これにより、$${\Sigma_u}$$の推定にコレスキー分解を使うことが可能になります。

長期制約(BQ制約)

この識別方法はあるショックは一つ以上の内生変数にたいして、長期の累積効果を持たないという理論に基づいています。以前の、貨幣の中立性の経済理論から、金融政策が産出にに長期での効果を持たないという解釈を思い出してください。

長期制約をどのように実装するか

長期制約をどのように実装するかを理解するために、まず時間を通じた累積ショックがどのようなものかを見ていきます。

まず、2変数のモデルを再び書きます。

$$
y_{1,t}= \phi_{11}y_{1,t-1}+\phi_{12}y_{2,t-1} +b_{11}\epsilon_{1,t}+b_{12}\epsilon_{2.t}\\
y_{2,t}=\phi_{21}y_{1,t-1}+\phi_{22}y_{2,t-1}+b_{21}\epsilon_{2,t}＋b_{22}\epsilon_{2,t}
$$

行列の形では以下のように表されます。

$$
Y_t= \Phi Y_{t-1} + B\epsilon_t
$$

次に$${T+1}$$期を考えていきます。

$$
Y_{t+1} = \Phi (\Phi Y_{t-1} + B\epsilon _t) + B\epsilon _{t+1} \\ = \Phi^2 Y_{t-1} + \Phi B \epsilon _t + B\epsilon _{t+1}
$$

$${Y_t}$$ を代入することで、

$$
Y_{t+1} = \Phi (\Phi Y_{t-1} + B\epsilon _t) + B\epsilon _{t+1} \\ = \Phi^2 Y_{t-1} + \Phi B \epsilon _t + B\epsilon _{t+1}
$$

同様に$${T+2}$$期を考えます。

$$
Y_{t+2} =\Phi Y_{t+1} + B \epsilon _{t+2}\\ =\Phi (\Phi^2 Y_{t-1} +\Phi B \epsilon _t + B\epsilon _{t+1}) + B\epsilon _{t+2} \\ = \Phi^3 Y_{t-1} + \Phi^2 B\epsilon_t + \Phi \epsilon _{t+1} + B\epsilon _{t+2}
$$

それぞれの各時点での$${\epsilon_t}$$の衝撃のみに注目すると、

長期の累積効果は、これらのショックの合計に等しくなります。

$$
B \epsilon _t + \Phi B \epsilon _t + \Phi^2 B \epsilon _t+...+\Phi^\infty B\epsilon _t = \sum^\infty _{i=0} = \Phi ^i B \epsilon _t
$$

データが、定常的である場合には、この事実を用いることができます。

$$
\sum^\infty _{i=0} \Phi^i = (1-\Phi )^{-1}
$$

これは$${\epsilon _t}$$の累積長期の効果が

$$
C= (1-\Phi ) ^{-1} B
$$

で与えられることを意味します。

長期制約を実装するためには、行列$${C}$$のある一つを0とすればよいことが分かります。

符号制約

符号制約の第一感はとてもシンプルで、あるショックが、一つ以上の内生変数の増減のみを引き起こすことを意味しています。

符号制約は原油価格のモデルの際によく用いられています。例えば、Kilian and Murphy(2012)では原油供給、総供給、原油のみの需要を調べるためにSVARモデルを用いています。彼らは符号制約を用いて、構造ショックを識別することを可能にしています。

符号制約をどうやって実装するか？

符号制約は回転行列を識別するために反復$${guess-and check}$$ 方法を用いて実装されます。行列$${Q}$$は行列$${B=PQ}$$となるように定義します。ここで、$${P}$$は短期制約の部分で議論した$${\Sigma_u}$$をコレスキー分解したものです。

当てはまる$${Q}$$の解は以下のアルゴリズムで見つけることができます。

ランダムな行列$${Q}$$を作る。
$${\sum_u}$$のコレスキー分解として$P$を計算する。
$${B}$$とそれに関連するショックの影響を計算する。
ショックが選んだ符号制約に整合的かを確認する。もし当てはまっていなければ、$${Q}$$を放棄して計算し直す。

良く用いられるSVARの識別方法のまとめ

結論

このブログでは、構造VARモデルの識別問題について、深く見てきました。ブログを呼んだ後に、以下のことが理解できるようになっているはずです。

構造形VARモデルと誘導形VARモデルの違い
構造形VARモデルと誘導形VARモデルの関係性
構造形VARの識別問題
構造形VARの識別問題へのよくある解決方法

日本語訳終わり

もし間違いなどあれば、教えていただけると幸いです。

この記事が気に入ったらサポートをしてみませんか？