
自由エネルギー原理について誰でもわかる、明快かつ深い解説 -1-
フリストン (K. J. Friston) の変分自由エネルギー原理(Free energy principle以下FEPと略します)はどんな原理で、どんなご利益があるのかについて順次解説していきます。
1.変分自由エネルギーの定義
フリストンは、自由エネルギー原理について、「自由エネルギー原理とは、環境と平衡状態にある自己組織化システムは、その自由エネルギーを最小にしなければならない、というものである。この原理は、基本的に適応システム(動物や脳などの生物学的要素)が、無秩序になる自然な傾向にどのように抵抗するかを数学的に定式化したものである。」と定義しています。
The free-energy principle says that any self-organizing system that is at equilibrium with its environment must minimize its free energy. The principle is essentially a mathematical formulation of how adaptive systems (that is, biological agents, like animals or brains) resist a natural tendency to disorder.
(Friston, K. J. (2010) The free-energy principle: a unified brain theory?)
これだけではわかるようなわからない感じですね。説明の順番はいろいろあると思いますが、実は、フリストンも述べているように、この主張の最大の価値は「数学的に定式化した」ことにあるので、式から始めるのが結局一番わかりやすいと考えました。数式に抵抗ある方も、その意味を順次解説して行きますので、しばし、お付き合いください。
変分自由エネルギー( VFE : variational free energy )の定義式は以下の通りになります。
VFE(変分自由エネルギー)
= DKL [q(x) || p(x, s)] (1)
= Σ [q(x)・log {q(x)/p(x, s)}] (2)
= Eq(x) [log q(x) - log p(x, s)] (3)
いきなり知らない記号が出てきて戸惑うかもしれませんが、どれも同じことを別の表記方法で書いているだけですから、(1), (2), (3)どれでもお好きな表記で考えていただければ結構です。
(1)式のDKLは、カルバックライブラー情報量(=相対エントロピー)と呼ばれる、確率分布どうしの近さを表す尺度です。常にDKL≧0であり、双方の確率分布が全く同じ(重なる)時に0となります。(2)式がその定義式です。またEは期待値で、Eq(x)は確率分布q(x)を重みとする期待値です。(確率分布の場合、期待値と平均値は同じです。)割り算は対数をとると、対数の引き算になる点にご注意ください。
*確率分布と期待値、カルバックライブラー情報量については、本記事最後のコラムにも書きました。
この段階で登場した変数はたった2つだけです。q(x)は認識の確率分布 (recognition density) と呼ばれます。q( )という表記をしていますが、p( )と同じく確率分布です。ただ、これだけではわかりにくいと思いますので、さきに、p(x, s)を説明します。
p(x, s)は同時確率分布を表します。これは、xという事象と、sという事象が、同時に起こる確率(の分布、以下まぎれのない場合は分布を省略します。)です。例えば、「泥棒が来た」という事象をx、「犬が吠えた」という事象をsとした時、「泥棒が来て、犬が吠えた」という事象の確率を表します。
ここで、p(x, s) = p(x | s) ・ p(s) = p(s | x) ・ p(x) という関係がなりたちます。これをベイズの定理と言います。 p(x | s) 、p(s | x)は条件付確率と呼ばれ、 p(x | s)は、犬が吠えた時(これが条件)泥棒が来ている確率を表します。同様に p(s | x)は、泥棒が来た時(これが条件)犬が吠えている確率を表します。
p(s)、p(x)は、その条件が起きる確率、すなわちp(s)は犬が吠える確率、p(x)は泥棒が来る確率です。(それぞれ周辺尤度と言います。)蛇足かもしれませんが、泥棒が来ても犬が吠えないこともあれば、犬が吠えても泥棒は来ていないこともあります。以上の関係をベン図で示すと図1のようになります。

次にq(x)の説明です。FEPでは、外界をより確実に推定(外界の不確実さを減ら)し、外界に対する予測の誤差を減らしていくことを目指します。外界に対する推定を順次更新していくわけです。そこで一時点前のp(x)q(x)が、現時点のp(x)q(x)となります。現時点のp(x)q(x)は次の時点のq(x)となります。イメージとしては図2のようになります。先の例で言えばq(x)は「泥棒が来ている」という事象の推定確率です。そんなものなぜわかるのかと思われるかもしれませんが、これは過去の経験つまり学習の結果による推定(ベイズ確率では事前確率と言います)だと考えてください。この推定を最新の事象による推定(ベイズ確率では事後確率と言います)で更新していくことこそが、FEPなのです。

2022/10/18 訂正 上記段落と図2が誤っていたので、修正しました。
p(x)→q(x)です。
2.変形1
Eq(x) [log q(x) - log p(x, s)] (3)
= Eq(x) [log q(x) – log {p(x | s)・p(s)}]
= Eq(x) [log q(x) – {log p(x | s) + log p(s)}]
= Eq(x) [log q(x) – log p(x | s) – log p(s)] (4)
= Eq(x) [log q(x)] – Eq(x) [log p(x | s)] + Eq(x) [– log p(s)]
= Eq(x) [log q(x)] – Eq(x) [log p(x | s)] – log p(s) (5)
推定値 条件付確率 周辺尤度
このベイズの定理を使って (3)式を書き換えると、(4)式のようになります。(しばらくは、p(x, s) = p(x | s) ・ p(s)だけを使って、p(x, s) = p(s | x) ・ p(x) は後回しにします。)すると登場する変数は同時確率が2つの変数の積に分解されたので、3つとなりました。掛け算は対数をとると、対数の足し算になる点にご注意ください。
さらに、(4)式を変形し、(5)式を得ます。log p(s)にはxが含まれていませんから、q(x)という重み付きの和はlog p(s)になる点にご注意ください。これはただの数学的変形(ただし、平均場近似という近似を行っています)なのですが、この変形によって、同時確率と推定値の関係を、条件付確率と推定値の関係と、その条件が起きる確率(周辺尤度)といいます)に分解することができました。このご利益が大きいのです。このご利益は、元はと言えばベイズの定理で同時確率を条件付確率と周辺尤度の積に分解したことによります。
(5)式をカルバックライブラー情報量を使って表すと、
Eq(x) [log q(x)] – Eq(x) [log p(x | s)] – log p(s) (5)
= DKL [q(x) || p(x | s)] – log p(s) (6)
となります。
ここまで定義式とその変形を元に話を進めてきました。ここで、自由エネルギー原理の意味を(6)式を元に説明します。冒頭にあげたフリストンの定義は、簡単にいうと「生物の知覚や学習、行動は自由エネルギーと呼ばれるコスト関数(=自由エネルギー)を最小化するように決まり、その結果生物は外界に適応できる。(磯村 2022)」という理論です。このコスト関数を求める式が(6)式です。
また、「生物は感覚入力の予測しにくさを最小化するように、内部モデルおよび行動を最適化し続けている。(磯村 2018)」とも言い換えることができます。これは、生物が外界の環境に適応して、恒常性(ホメオスタシス)を維持するためには、新しい驚き(surprise)に出会った時、それを学習して、次からは驚きを減らすような内部モデル(生成モデル)を構築・更新し、行動していかなければならないという主張です。そのための方法は(6)式の第1項を減らすこと(これが内部モデルの更新です)と第2項(これが驚きにあたります)を減らすことです。自由エネルギーを減らすにはこの2つの方法をバランスよく実行する必要があるということになります。
なぜバランスよく実行する必要があるか、数式的にはいずれお話したいと思いますが、今はこのように考えてみてください。自由エネルギー最小化のプロセスは、仮説検証のプロセスに似ています。人が行動を起こすのは、何らかの仮説があるからです。仮説なしでは何も始まりません。そして、行動によってその仮説を検証します。行動(検証)の結果、仮説が支持されれば仮説はより確からしいものとして強化されます。仮説に反するような結果が出た場合は仮説を修正します。人は、この仮説と検証の繰り返しによって徐々に世界の真実に近づいていくのです。この時、例えば検証せずに仮説だけを過度に精緻化していったり、仮説を変えずに検証を過度に繰り返すことは、非効率なのです。ある程度仮説を進化させたら検証する。ある程度データを集めて検証したら仮説を修正する。といった方法をとる方が効率的なのです。このイメージを図3に示しました。(6)式の第1項は内部モデルによる仮説と推定値の距離を縮めること、第2項は能動的推論で驚き(surprise)を最小化することに対応しています。この両者を交互に順次減らしていくイメージがつかめるでしょうか。

本記事では、FEPとは何かについて、最低限の説明をしましたがおわかりいただけだでしょうか。次回はもう一つの変形について説明したいと思います。
参考文献
Friston, K. J. (2010) The free-energy principle: a unified brain theory?
磯村拓哉 自由エネルギー (2022) 脳科学辞典
自由エネルギー原理 - 脳科学辞典 (neuroinf.jp)
磯村拓哉 自由エネルギー原理の解説 (2018) 日本神経回路学会誌
https://www.jstage.jst.go.jp/article/jnns/25/3/25_71/_pdf
HEADBOOST「確率分布を誰でも理解できるようにわかりやすく解説」
https://www.headboost.jp/what-is-probability-distribution/
乾 敏郎 感情とはそもそも何なのか (2018) ミネルヴァ書房
乾 敏郎 坂口 豊 脳の大統一理論 (2020) 岩波書店
乾 敏郎 坂口 豊 自由エネルギー原理入門 岩波書店 (2021)
Thomas Parr, Giovanni Pezzulo, Karl J. Friston (2022) Active Inference
( 乾 敏郎(訳)能動的推論 (2022) )
国里愛彦 他 計算論的精神医学 (2019) 勁草書房
コラム1:確率分布と期待値、カルバックライブラー情報量
日本の小中高では、確率と統計についてはある程度まで習います。小学校ですら、確率は、場合の数と割合について6年生で習います。統計に関しては、棒グラフは3年生で登場し、6年生では度数分布表、ヒストグラムも習います。しかし、確率と統計は別々に習って来ました。今は高校の数学Bで、確率分布が登場するようですが、大学入試に出ないということであまりしっかりとは習わないようです。それで、大学の統計学の講義でいきなり確率分布が出てきて面食らうのです。しかし、確率分布は、確率を統計学的観点から定義し直したもので、簡単な例で考えれば難しくありません。
今、コイン投げで確率を考えてみます。普通のコインでは、表が出る確率は約0.5です。確率の総和は1なので、裏が出る確率は1-0.5=0.5となります。1枚のコイン投げでは。場合の数が表と裏の2なので、確率分布を考える必要はないかもしれませんが、あえて確率分布で表現すると図4のようになります。棒グラフですね。

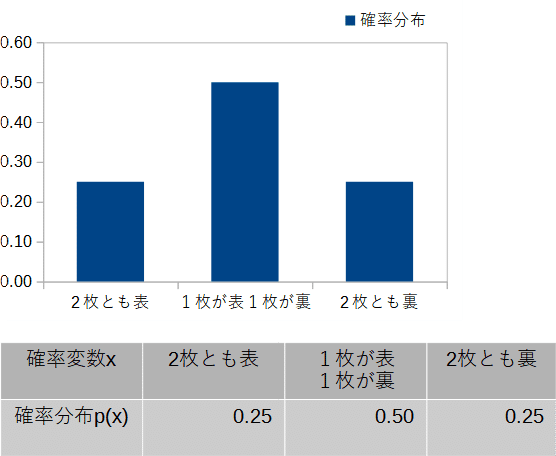
今度は2枚のコイン投げで考えると、2枚とも表が出る確率は0.5×0.5=0.25であり、2枚とも裏が出る確率も0.5×0.5=0.25です。そして表と裏が1枚づつ出る確率は、1-0.25-0.25=0.5となります。これを確率分布で表したのが図5です。このように場合の数が3以上になると確率分布の考え方が必要です。
さらに、アンケートなどで選択肢が多くあり、それぞれの選択肢を選んでもらった場合の確率分布を表したのが図6です。棒グラフにすれば分かりやすいですね。 確率分布については、下記のサイトの説明が詳しくてわかりやすいので、興味のある方は参照してください。

HEADBOOST「確率分布を誰でも理解できるようにわかりやすく解説」https://www.headboost.jp/what-is-probability-distribution/
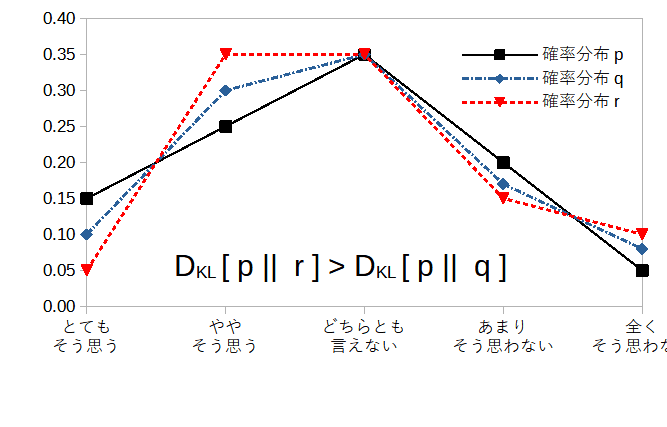
次にカルバックライブラー情報量ですが、これは確率分布どうしの近さを表します。単なる確率ならば、50%と60%は10ポイント差などと単純に言えますが、確率分布だとそうはいきません。ですから、定義式(2)のような計算をして近さを判断します。図7に3つの確率分布を示しました。真ん中の「どちらともいえない」の確率は同じですが、その他の選択肢の確率は異なっています。この時、確率分布rから見た確率分布pよりも、確率分布qから見た確率分布pの方が「距離」が近いと言えます。ただし、カルバックライブラー情報量はどちらの確率分布から見るかで値が変わるので、正確には「距離」とは言えません。(定価1000円の商品の2割引は800円で、その差は200円ですが、割引後の売価800円の2割増しは、960円と差が160円になることと同じ理屈です。)
自由エネルギー原理について誰でもわかる、明快かつ深い解説 -2- 公開しました。
この記事が気に入ったらサポートをしてみませんか?
