
ベイズ統計モデリングに挑戦~重回帰モデル~
前回までの取り組みでは単回帰をベイズ統計モデリングによって行いました。単回帰を行った記事はこちら↓。
今回はさらなる発展として重回帰のモデルに取り組んでいきます。また、これでまはStanを用いてMCMCサンプリングを行っていましたが、今回はbrmsを用いてMCMCサンプリングを行っています。
今回の統計モデルを実施するにあたりイメージした環境は↓のようになっています。

テストの成績に、身体活動量と体格の2要因がどのように関わっているか検証していきます。これらのデータは乱数発生によって作成した疑似データとなっています。
データセットの生成
データセットの生成に関しては、↓のコードにより作成しました。
#データセット
#スコアの乱数生成
ta=rnorm(20,50,10) #正規分布:平均50で標準偏差10の乱数
tb=rnorm(20,65,10) #正規分布:平均65で標準偏差10の乱数
tc=rnorm(20,80,10) #正規分布:平均80で標準偏差10の乱数
#身体活動量の乱数生成
ea=rnorm(20,20,5) #正規分布:平均80で標準偏差10の乱数
eb=rnorm(20,40,5) #正規分布:平均80で標準偏差10の乱数
ec=rnorm(20,60,5) #正規分布:平均80で標準偏差10の乱数
#BMIの乱数生成
ra=as.integer(runif(20,min=1,max=4)) #整数:1~3で乱数生成
rb=as.integer(runif(20,min=1,max=4)) #整数:1~3で乱数生成
rc=as.integer(runif(20,min=1,max=4)) #整数:1~3で乱数生成
#データフレームの作成
data1=data.frame(ta,ea,ra)
data2=data.frame(tb,eb,rb)
data3=data.frame(tc,ec,rc)
#データフレームの列名変更
names(data1) <- c("score", "physical_activity","BMI")
names(data2) <- c("score", "physical_activity","BMI")
names(data3) <- c("score", "physical_activity","BMI")
#データフレームの結合
data12=rbind(data1,data2)
data_all=rbind(data12,data3)
#BMIのラベル付け
trans <- function(x) {
BMI <- c("1"="痩せ", "2"="標準","3"="肥満")
BMI[as.character(x)]
}
data_all[,3] <- trans(data_all[,3])
適切にデータセットが作成できたか、一応確認してみます。
#データセットの確認(初めの6行)
head(data_all)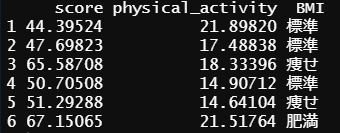
score(テストの成績)という目的変数と、physical_activity(身体活動量)とBMI(体格)という説明変数が作成できたことが確認できました。
図の作成
どのようなデータセットか図示してみます。まずは箱ひげ図から作成してみます。
#箱ひげ図作成のためのコード
ggplot(data = data_all, mapping = aes(x = BMI, y = score)) +
geom_boxplot() +
geom_point(aes(color = BMI)) +
labs(title = "身体活動量とテスト成績の関係")
箱ひげ図をみてみると、テストの点数は、痩せ→肥満→標準という順番であることが分かります。
散布図も作成してみます。
#散布図作成のためのコード
ggplot(data=data_all, aes(x =physical_activity, y = score, colour=BMI)) +
geom_point() +
geom_smooth(method = "lm", se = FALSE)+
labs(title = "身体活動量とテスト成績の関係")
散布図をみると、身体活動量が高いほどテストのスコアが高くなっていることが分かります。また、痩せの体格は他の体格よりもテストのスコアが高くなっていることが分かります。
このように図で確認した現象が実際に生じているのかについて、ベイズ統計モデリングによって検証していきます。
重回帰モデル
今回の一般線形化モデル(重回帰モデル)は次のように設定しました。分布は正規分布に従っていると仮定しました。
μi=β0+β1*xi1+β2*xi2+β3*xi3、yi~Normal(μi, σ^2)
xi1にはBMI肥満、xi2にはBMI標準、xi3には身体活動量が入るようになっています。ここで、BMIは3つ(痩せ、標準、肥満)あるのにモデル式には2つしか使ってないじゃんと思われた方はダミー変数というのを勉強していただけると、このモデルが理解できると思います。
これらのことから、モデルの構造式は
scorei ~ Normal(Intercept+beta1*BMI肥満+beta2*BMI標準+beta3*physical activity, sigma^2)
このデータセットを用いてベイズ統計モデリングにおける重回帰を実行してみました。詳しいコードは、【馬場真哉 (2019).「実践Data Scienceシリーズ RとStanではじめる ベイズ統計モデリングによるデータ分析入門」講談社】という書籍を参考にしています。そのため、ここではコードの記載は省略します。
結果は↓のようになりました。

BMIが肥満や標準の場合は、痩せに比べてネガティブな影響を与えていること(BMI肥満:-6.95、BMI標準 : -9.25)が分かりました。身体活動量が高いほどテストのスコアが高くなることが判明しました(physical_activity:0.7)。これは、最初に図示したときに考えた結果と一致していますね。
ここで、モデルの収束についても確認しておきます。

結果の欄でのRhatはすべて1であることから収束していることが分かります。また、トレースプロットからモデルが収束していることが分かります。
最後に事後分布の回帰直線を図示しておきます。

この図からもBMIが痩せで身体活動量が高いほどテストのスコアが高くなることが分かりますね。
と今日はここまでとします。次回はロジスティック回帰モデルを実行していきたいと考えています。
注意:本記事では乱数発生によってデータセットを作成しています。そのため、本記事での結果が一般的な現象の結果を表しているわけではございませんのでご注意ください。
最後まで読んでいただきありがとうございました。
参考資料
参考文献・資料
・馬場真哉 (2019).「実践Data Scienceシリーズ RとStanではじめる ベイズ統計モデリングによるデータ分析入門」講談社
・Rでラベルの読み替え(数値⇔ラベルの変換)
https://qiita.com/ryamamoto0406/items/4d0e35b2583b186249f7
ベイズ統計に関してはまだまだ勉強中の身ですので、データの記載や解釈等に間違いがありましたら、ぜひコメント等で教えてください。
