
構造方程式モデリング①~媒介分析による間接効果について~
1. はじめに
現在、構造方程式モデリング(SEM: Structural Equation Modeling)について学んでいます。「構造方程式モデリング」という名前がカッコいいですよね!この名前だけでも、このモデリングについて学びたいと思ってしまいます。今学んでいる構造方程式モデリングの知識の整理としてこのnoteを書いています。「ここの表現がおかしい」や「その説明は間違っている」があればぜひご指摘ください。さて、早速始めていきましょう!
この度大変ありがたいことに、本記事の間違い点をご指摘いただきました。本当にありがとうございます。この場をお借りして感謝申し上げます。一つ目としては、一方方向の関係性のみが因果を関係を表すということではないということです。二つ目にはSEMによって因果が判明するという点は注意が必要だということでした。ご指摘いただいた点は、自分だけでなく他の方も間違えている可能性があるかと思い、本記事では修正の線を引いていますが間違い箇所を残しています。私と同じような間違いを犯さないためにも、本記事を利用していただければと思います。
2. 構造方程式モデリング
構造方程式モデリングは別名で共分散構造分析とも言います(名称の詳細については、参考資料[1]をみてみてください)。このモデルを使うことで因果関係を推論することができます。得られた変数同士にどのような関連が存在しているのかを明らかにして、一つの変数の数値が変化すると関連した変数がどのように変化するのかという考察につながります。「関連」という言葉を聞くと相関じゃないと思いますね。ここに例えば、Xという変数とYという変数があったとします。相関と言うのはXとYの双方の関係性を見ています。そのイメージを下図に示します。

一方で因果関係は変数Xの値によってYの値にどのような影響を及ぼすかという関係を示しています。相関関係が双方向の関連だったとに対して、因果関係は一方方向の関係になります。(一方方向性で因果とは言い表せないそうです。ここは完全に私の間違いです。当然下の図も間違っています。間違えるのも勉強と一環ということで、ここではこの間違えを残しておきます。)

この図をみるとおそらく、「これって回帰モデルじゃん」と思う方がいらっしゃると思います。そうです。回帰モデルで表せるんです。ただ回帰モデルの主眼は”予測”に着目しています。そこが因果関係との大きな違いになっています。つまり、ある変数Xからある変数Yへの関係性を示そうと考えた時には因果関係を考える必要があります。この因果関係を捉える統計的な手法として構造方程式モデリングを用います。(構造方程式モデリングを行えば、因果を証明できるといわけではないので注意が必要です)
3. 媒介分析による間接効果
3.1. 重回帰モデル
ここで問題です。「複数の説明変数と1つの目的変数があります。説明変数と目的変数の関連について調べたい場合はどのような統計解析を行うべきでしょうか?」。おそらく多くの方が、「重回帰分析による統計解析」という手法を選択されると思います。私も、構造方程式モデリングを勉強するまでは重回帰分析で行うことしか選択肢がなかったです。変数というと抽象すぎてイメージしづらいので、ここでは具体的な事例として、身体活動とBMI(体格指数:体重を身長の2乗で割った数値)と認知機能(注意や記憶といった脳機能)という3つの変数を使っていきます。ここでは、身体活動とBMIが説明変数、認知機能を目的変数とします。説明変数とは、変数として説明している役割を担い、目的変数とは明らかにしたい事象の目的となる変数となります。認知機能に対して、身体活動とBMIがどのように関係しているのかを見ていきます。まずは、最初にでてきた重回帰という回帰モデルを考えます。イメージを下図に示しています。

重回帰では↑の図から分かるように、認知機能に対して身体活動とBMIがどのような影響を与えている(どのような関連が存在する)のかを明らかにするモデルになります。つまり、身体活動量が多いと認知パフォーマンス(認知機能を評価するテストの点数といったパフォーマンスの数値)が高いのかもしくは低いのかといった観点や、BMIが高いと認知パフォーマンスが高いのかもしくは低いのかということを検証することができます。また、作成したモデルから、どれくらい身体活動量やBMIが高いと、認知パフォーマンスがどの程度になるのかといった予測を立てることができます。重回帰分析では偏回帰係数というのを算出してモデルの関連をみていきます。この偏回帰係数とは、他の説明変数を固定した場合に、ある説明変数が1上がると(もしくは下がると)目的変数の値はどう変化するのかということを示す指標になります。たとえば、今回の事例では、BMIの値を固定した場合に、身体活動量が1上がると認知パフォーマンスがどのように変化するのかといったことが分かります。
3.2. 媒介分析による間接効果
ただここで、上記に示した身体活動とBMIと認知機能という関係において、先行研究から身体活動量が高いと認知パフォーマンスが高いといった関係が存在していることが判明しているとします。加えて、どうやらこの関係(身体活動量と認知パフォーマンスとの因果関係)にBMIが影響を及ぼしているんじゃないかということが疑問となり、その影響について明らかにしたいときには、構造方程式モデリングよる媒介分析を行う必要がでてきます。上記の記載を図に表すと下の図のようになります。
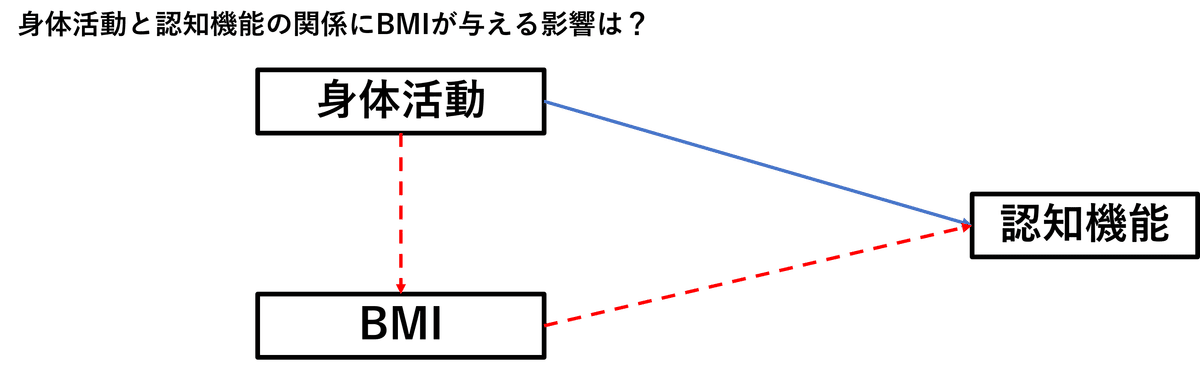
図で示すところの赤い点々の経路の関係を明らかにしたいという場合には、上記に示した重回帰モデルではその経路が存在しないため検討できません。そのため、モデルとしては同じような回帰モデルに見えても媒介分析を行う必要があります。
媒介分析は回帰モデルでも遂行することができます。その詳しい説明に関しては、参考資料[4]を見ていただければと思います。回帰モデルに慣れている場合は、媒介分析の説明は構造方程式モデリングからのアプローチよりも回帰モデルからのアプローチの方が親しみやすいかと思います。
このモデルでいうBMIが身体活動量と認知機能との媒介する役割を担っていることから、媒介変数と言います。この媒介変数を用いて因果関係を推論する統計手法を媒介分析と言います。この媒介変数を通した身体活動と認知機能との因果を間接効果といいます(赤の点線)。身体活動と認知機能との因果を直接効果(青の実践)と言います。この間接効果と直接効果を合わせた効果を身体活動と認知機能との全体的な効果として、総合効果と言います。
間接効果、直接効果、総合効果についての詳細は、参考資料[1]・[2]・[5]・[11]を見ていただけると理解が深まります。
3.3. Rによる媒介分析の実装
ここまでで構造方程式モデリングや媒介分析の説明が一通り終わりました。説明を聞いているだけでは「はて何のこと?」で終わってしまいます。実際にプログラミングによって分析を行い結果を考察することで、さらなる理解につながります。ここでは、フリーソフトであるRとそのパッケージであるlavaan(参考資料[6])を用いて、実際に媒介分析による間接効果を明らかにしていきます。
今回使用するパッケージとしては、以下のパッケージを使います。lavaanは構造方程式モデリングに使用するパッケージで、semPlotは作成したモデルのパス図を作成するパッケージです。
library(lavaan)
library(semPlot)
#パッケージのインストールに関しては、install.packages()というコマンドを使用するとできます。
#例えば、lavaanをインストールするのであれば、install.packages("lavaan")といった感じです 3.3.1. 疑似データの作成
まずはデータの作成です。データは乱数発生によって作成した疑似データを用います。疑似データを作成するに当たってイメージした設定を下図に示しています。

では、上記の想定した設定で疑似データを作成していきます。疑似データ作成のコードを↓に示します。
#データセット
#スコアの乱数生成
set.seed(1234)
ta=rnorm(20,50,10) #正規分布:平均50で標準偏差10の乱数
tb=rnorm(20,65,10) #正規分布:平均65で標準偏差10の乱数
tc=rnorm(20,80,10) #正規分布:平均80で標準偏差10の乱数
#身体活動量の乱数生成
ea=rnorm(20,20,5) #正規分布:平均20で標準偏差10の乱数
eb=rnorm(20,40,5) #正規分布:平均40で標準偏差10の乱数
ec=rnorm(20,60,5) #正規分布:平均60で標準偏差10の乱数
#BMIの乱数生成
ra=rnorm(20,43,2) #正規分布:平均38で標準偏差2の乱数
rb=rnorm(20,38,2) #正規分布:平均30で標準偏差2の乱数
rc=rnorm(20,22,2) #正規分布:平均22で標準偏差2の乱数
#データフレームの作成
data1=data.frame(ta,ea,ra)
data2=data.frame(tb,eb,rb)
data3=data.frame(tc,ec,rc)
#データフレームの列名変更
names(data1) <- c("SC", "PA","BMI")
names(data2) <- c("SC", "PA","BMI")
names(data3) <- c("SC", "PA","BMI")
#データフレームの結合
data12=rbind(data1,data2)
data_all=rbind(data12,data3)ここでは認知パフォーマンスをSC(Score)、身体活動をPA(Physical Activity)、BMIはそのままBMIとしています。乱数発生は恣意的しているので、実際の研究の知見と異なることがありますので、ご注意ください。
3.3.2. モデルの作成
図4でイメージしたモデルを作成していきます。コードは↓のようになっています。
model <- ' SC ~ c*PA
BMI ~ a*PA
SC ~ b*BMI
ab := a*b
total := c + (a*b)' ここでは、cが直接効果、a*bが間接効果、c+a*bが総合効果となっています。SCという目的変数、PAという説明変数、BMIという媒介変数があり、それらの係数としてa・b・cとなっています。イメージしやすりようにそれぞれの変数と係数の関係を下図に示しています。

モデル作成の詳細については、参考資料[2]・[6]・[7]・[8]・[9]・[10]を見ていただけると理解が深まります。
3.3.3. モデルの分析
作成したモデルの分析を行っていきます。今回は、lavaanのsem()という関数を用いて分析を行います。
fit <- sem(model, data = data_all)作成したモデルの結果をみてみます。今回は95%信頼区間を出すためにci=TRUEとしています。このほか、モデルの適合率などを見る場合には、fit.measure=TRUEという記載をいれることで確認できます。また、標準誤差をブーストラップ法を用いてサンプリングによって算出するには、se = "bootstrap"の記載を加えることで実行できます。
summary(fit,ci=TRUE)結果の出力は↓のようになりました。
Regressions:
Estimate Std.Err z-value P(>|z|) ci.lower ci.upper
SC ~
PA (c) 0.470 0.160 2.942 0.003 0.157 0.783
BMI ~
PA (a) -0.499 0.032 -15.446 0.000 -0.562 -0.435
SC ~
BMI (b) -0.489 0.286 -1.709 0.088 -1.051 0.072
Variances:
Estimate Std.Err z-value P(>|z|) ci.lower ci.upper
.SC 79.888 14.585 5.477 0.000 51.301 108.475
.BMI 16.222 2.962 5.477 0.000 10.417 22.027
Defined Parameters:
Estimate Std.Err z-value P(>|z|) ci.lower ci.upper
ab 0.244 0.144 1.698 0.089 -0.038 0.526
total 0.714 0.073 9.736 0.000 0.570 0.858
直接効果(c)は0.47、間接効果は0.244、総合効果は0.714となりました。つまり、身体活動と認知パフォーマンスとの関連の推定値は0.47に対して、媒介変数であるBMIを介すとその推定値が0.244になることが分かりました。本当の研究であれば、間接効果のp値をみて、間接効果が統計的に有意であったかについて評価する必要があります。今回は乱数発生による疑似データなので、p値の評価は問題にしないことにします。
媒介効果や直接効果の評価に関しては、参考資料[10]・[11]・[12]をみると理解が深まると思います。
3.3.4. パス図の作成
最後に分析したモデルのパス図を作成します。パス図の作成は、semPaths()を使うと簡単に描けます。ただ、まだまだ自分の知識不足で思い描くような柔軟な図はかけないので、描写されるパス図は参考程度にとどめています。
semPaths(fit, style="lisrel", whatLabels="est",
layout="tree", rotation=2, edge.label.cex=0.8)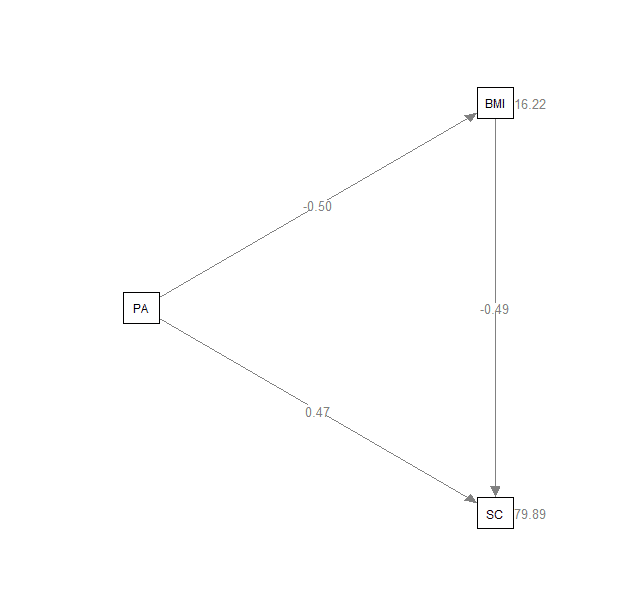
semPaths()を用いたパス図の作成については、参考資料[2]をみると理解が深まると思います。
3.3.5. 媒介変数の増加
ここまでで一通り媒介分析をRを用いて実装できるようになりました。実際の分析の場では、媒介変数が複数存在することもあるかと思います。そこで最後におまけとして、媒介変数をもう一つ増やして媒介分析を行ってみます。疑似データとして睡眠時間(SLP)を追加したデータセットを作成します。
set.seed(1234)
#睡眠時間の乱数生成
sa=rnorm(20,2,1) #正規分布:平均2で標準偏差2の乱数
sb=rnorm(20,5,1) #正規分布:平均5で標準偏差1の乱数
sc=rnorm(20,10,1) #正規分布:平均10で標準偏差1の乱数
#データフレームの作成
data11=data.frame(ta,ea,ra,sc)
data22=data.frame(tb,eb,rb,sc)
data33=data.frame(tc,ec,rc,sc)
#データフレームの列名変更
names(data11) <- c("SC", "PA","BMI","SLP")
names(data22) <- c("SC", "PA","BMI","SLP")
names(data33) <- c("SC", "PA","BMI","SLP")
#データフレームの結合
data123=rbind(data11,data22)
data_all_2=rbind(data123,data33)モデルの作成を行います。
model2 <- ' SC ~ c*PA
BMI ~ a1*PA
SLP ~ a2*PA
SC ~ b1*BMI
SC ~ b2*SLP
ab1 := a1*b1
ab2 := a2*b2
total := c + (a1*b1) + (a2*b2)' 上記のモデルの作成には、参考資料[9]に記載のコードを使用させていただきました。
モデルの分析を行います。
fit3 <- sem(model2, data = data_all_2)
summary(fit3,ci=TRUE) 結果は↓のようになりました。
Regressions:
Estimate Std.Err z-value P(>|z|) ci.lower ci.upper
SC ~
PA (c) 0.503 0.157 3.200 0.001 0.195 0.811
BMI ~
PA (a1) -0.499 0.032 -15.446 0.000 -0.562 -0.435
SLP ~
PA (a2) -0.002 0.008 -0.230 0.818 -0.017 0.013
SC ~
BMI (b1) -0.429 0.282 -1.522 0.128 -0.982 0.124
SLP (b2) 1.658 1.172 1.414 0.157 -0.640 3.956
Variances:
Estimate Std.Err z-value P(>|z|) ci.lower ci.upper
.SC 77.367 14.125 5.477 0.000 49.682 105.052
.BMI 16.222 2.962 5.477 0.000 10.417 22.027
.SLP 0.938 0.171 5.477 0.000 0.603 1.274
Defined Parameters:
Estimate Std.Err z-value P(>|z|) ci.lower ci.upper
ab1 0.214 0.141 1.514 0.130 -0.063 0.491
ab2 -0.003 0.013 -0.227 0.820 -0.029 0.023
total 0.714 0.073 9.785 0.000 0.571 0.857最後にパス図を書いておきます。
semPaths(fit3, style="lisrel", whatLabels="est",
layout="circle2", rotation=1, edge.label.cex=0.8)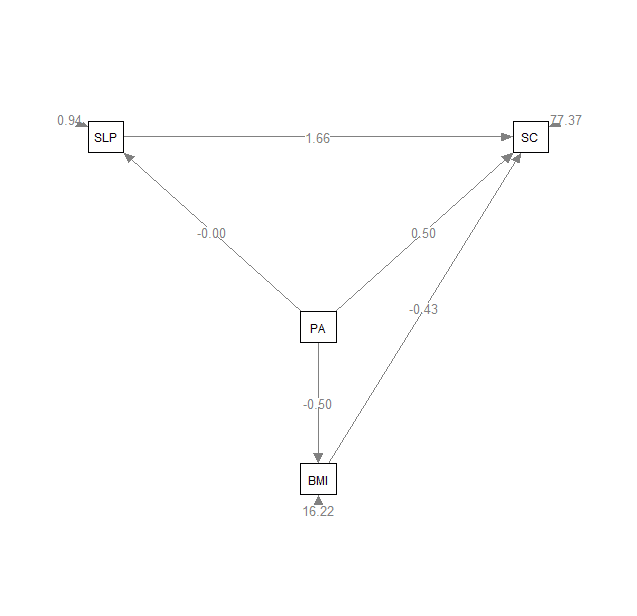
4. おわりに
最後まで読んでいただき誠にありがとうございました。読んでいただいた方に少しでもお役に立てる記事になっていればこれほど嬉しいことはありません。構造方程式モデリングをはじめとした統計を日々勉強している身として、まだまだ知識不足を実感しています。今回はできる限り分かりやすいように媒介分析について説明しました。おそらく、ところどころ理解しづらい点があったと思います。その際にはぜひ遠慮せずにご質問していただければと思います。また、説明やコードの改善点・間違いがありましたらご指摘していただけると非常にありがたいです。また、下記に記した参考資料に加えて、構造方程式モデリングを勉強するのに参考になる図書・論文・Webページがありましたら、ぜひご教示お願いいたします。
5. 参考資料
[1] 豊田 (1998) 共分散構造分析 入門編―構造方程式モデリング (統計ライブラリー) 朝倉書店
[2] 豊田 (2014) 共分散構造分析[R編]―構造方程式モデリング 東京書籍
[3] 小川(2020) つくりながら学ぶ! Pythonによる因果分析 ~因果推論・因果探索の実践入門 (Compass Data Science) マイナビ出版
[4] 村山 (2009) 媒介分析・マルチレベル媒介分析 https://koumurayama.com/koujapanese/mediation.pdf
[5] 矢田ほか (2020) 反事実モデルに基づく直接効果と間接効果の推定. 計量生物学, 40(2), 81-116.
[6] Rosseel, Y. (2012). lavaan: An R package for structural equation modeling. Journal of statistical software, 48, 1-36.
[7] 井出草平の研究ノート 媒介変数と間接効果と総合効果[R] https://ides.hatenablog.com/entry/2020/08/09/171118
[8] Rで構造方程式モデリング https://qiita.com/fujino-fpu/items/ed4c77a8ef47f116f1c2
[9]関西学院大学 社会学研究科 柏原 宗一郎のWebサイト
Rとlavaanパッケージで構造方程式モデリング・媒介分析、ブートストラップのサンプル数指定 https://kscscr.com/archives/r-and-lavaan-sem-mediation-bootstrap.html
[10] Ballen et al. (2021). Mediation analysis in discipline-based education research using structural equation modeling: beyond “what works” to understand how it works, and for whom. Journal of microbiology & biology education, 22(2), e00108-21.
[11] Sunny side up! 媒介分析と間接効果の検討 https://norimune.net/619
[12]Yang et al. (2022). Physical activity and social support mediate the relationship between chronic diseases and positive mental health in a national sample of community-dwelling Canadians 65+: A structural equation analysis. Journal of Affective Disorders, 298, 142-150.
注意:本記事では乱数発生によってデータセットを作成しています。そのため、本記事での結果が一般的な現象の結果を表しているわけではございませんのでご注意ください。
