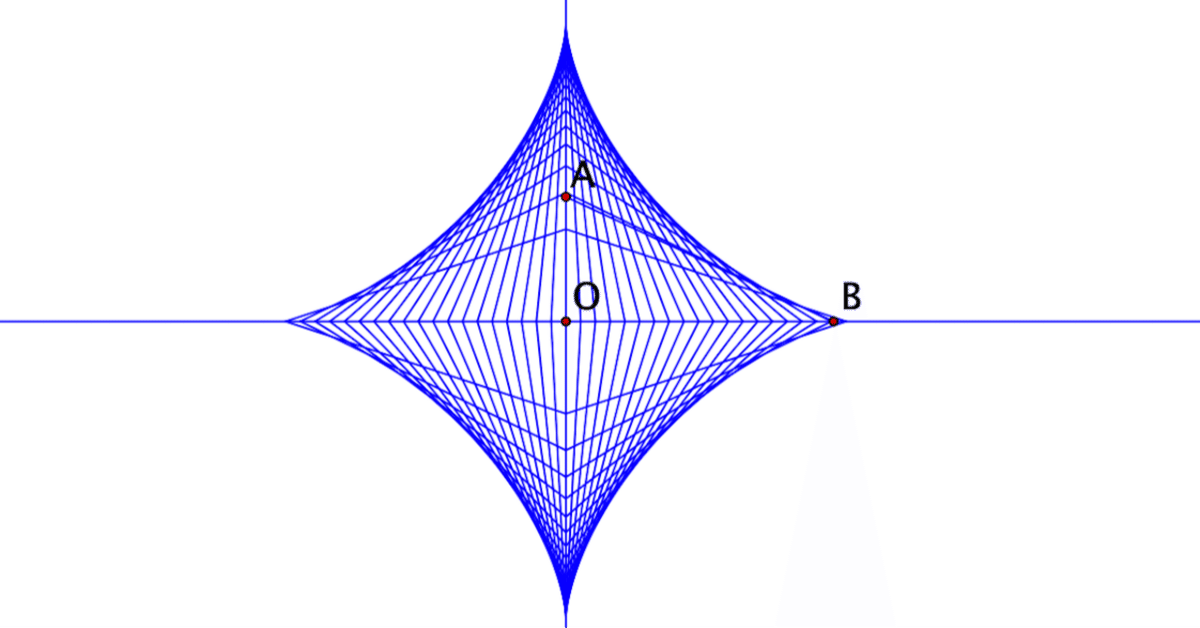
Cinderellaで数学:いろいろな曲線:アステロイド
アステロイドは結構知られた曲線で,ハイポサイクロイドで出てきたり,媒介変数表示が高校の教科書に出てきたりします。
「曲線の事典」(礒田正美他・共立出版2009)にはアステロイドの作図器が載っていますが,アステロイドだけでなく楕円なども描くものです。
点Oで交わる溝(直線)m,nがのっている平面$${\pi}$$がある。平面$${\pi}$$上に重ねられた平面$${\tau}$$には溝に沿って動く棒(線分)AB=bが取り付けられている。
平面は軸が直交している場合と斜交している場合の2とおりがあります。
A 軸が直交している場合
溝m,nが直交するとき,次の性質がいえる。
1. AB が動くとき、平面$${\tau}$$上の任意の点の軌跡は平面$${\pi}$$上に楕円になる。
2. ABが動くとき,ABは平面$${\pi}$$上にアステロイドの包絡線である。
3. 点Oが線分ABを直径とする円をかくとき,平面$${\pi}$$上の任意の点Pは、平面$${\tau}$$上にパスカルのリマソンをかく。
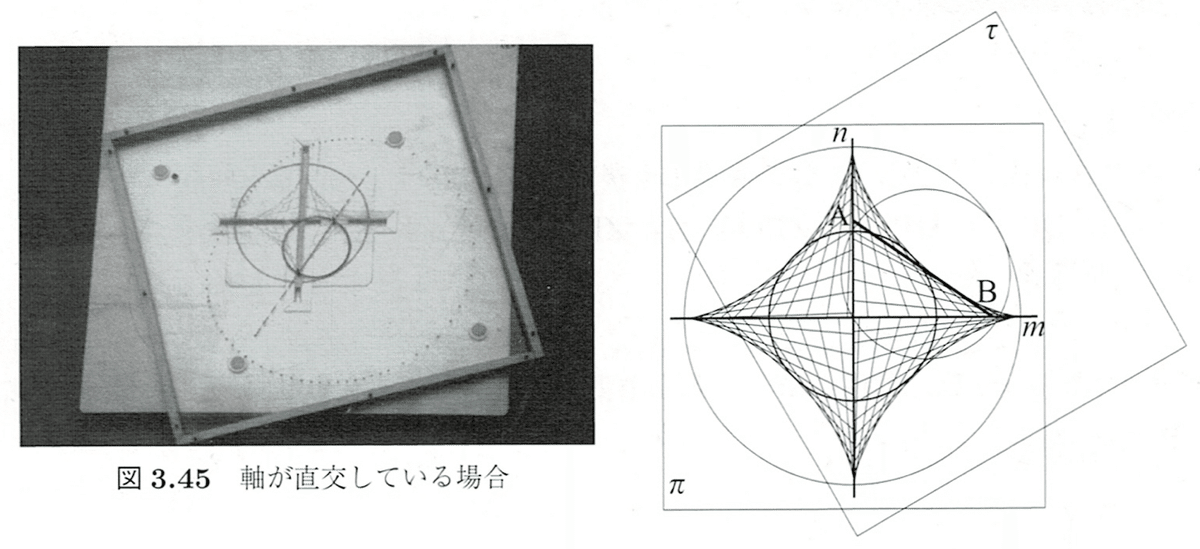
Web上ではこちらに写真があります。
リンク先に行ったら,「円錐曲線」のページに進みます。スクロールしていくと,アステロイドがあります。
では,順番にCinderellaで作図しましょう。
1. AB が動くとき、平面$${\tau}$$上の任意の点の軌跡は平面$${\pi}$$上に楕円になる。
「点Oで交わる溝(直線)m,nがのっている平面$${\pi}$$」を,背景に合わせて軸と原点をとります。y軸上の適当なところを中心として,固定した半径の円をかきます。半径は4としました。x軸との交点をとれば,「溝に沿って動く棒」ができます。作図手順によりFGとなっています。(手順によって名前が異なります)

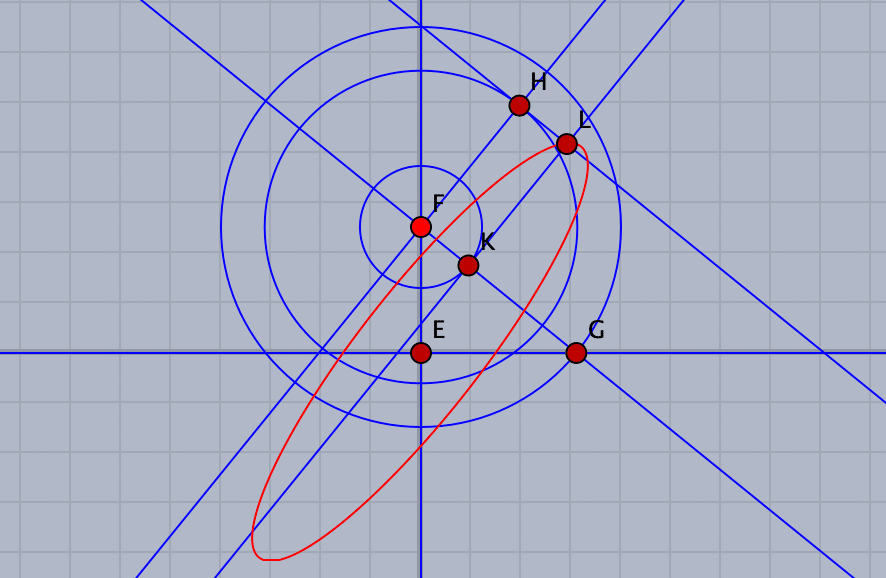
次に,「平面$${\tau}$$上の任意の点」を取るのですが,このままでは平面$${\tau}$$上にはとれません。平面$${\tau}$$を決めるために,FGを直線で結んで平面$${\tau}$$のx軸とし,垂線を引いてy軸とします。平面$${\tau}$$上に点を取るためには,このx軸,y軸に対して点を取るので,適当なところで各軸から垂線を引いてその交点をとります。適当といっても,点Fからの距離が変化しては行けないので,Fを中心とした円を描いて,交点をとってからその点で垂線を引きます。すると,点Fを動かしたときに平面$${\tau}$$が動き,平面$${\tau}$$上の点も同時に動くことになります。下図の点Lです。

軌跡ツールを選び,動かす点としてFを,軌跡を描く点としてLを選ぶと軌跡の楕円が描かれます。平面$${\tau}$$上の点の位置を変えるためには,補助円をドラッグします。
2. ABが動くとき,ABは平面$${\pi}$$上にアステロイドの包絡線である。
座標軸を取り,固定した半径の円を描くところまでは先ほどと同じです。原点は取らなくても構いません。今度はFとGを直線ではなく線分で結びます。

AB(作図上はFG)を動かして包絡線を描くのですが,Cinderellaには「足跡を描く」というものがあるのでこれを使いましょう。インスペクタを開き,線分FGを選んだら,「特別な表示方法」で「足跡を描く」にチェックを入れます。

点Fをドラッグすると,線分が動いたあとが描かれ,包絡線のアステロイドが見えてきます。点Fを半径より上に持っていくとGの位置が左右反転するので第2象限ににも描かれます。ただし,すべての軌跡が残るわけではなく,前のものは消えていくので「足跡の長さ」を最大にしてもすべての象限にきれいに描くことはできません。

4つの象限にわたって描くには,CindyScriptで描きます。
Gのx座標に対し,Fのy座標は$${\sqrt{4^2-x^2}}$$ で求められます。
x = 0.2;
while(x < 4,
y = sqrt(16 - x^2);
draw([[x, 0],[0, y]]);
draw([[-x, 0],[0, y]]);
draw([[x, 0],[0, -y]]);
draw([[-x, 0],[0, -y]]);
x = x + 0.2;
);xの増分により密度は変わります。次の図では補助円を水色にしましたが,非表示にしてもよいでしょう。

3. 点Oが線分ABを直径とする円をかくとき,平面$${\pi}$$上の任意の点Pは、平面$${\tau}$$上にパスカルのリマソンをかく。
意味がわかりにくいのですが,Oを円周上で動かして平面$${\pi}$$の方を回転させるというわけです。したがって,円周上の点Oと,その動きに合わせて動く座標軸をとる(平面$${\pi}$$)ことにします。ベースとなる平面は,いままではCinderellaの描画面でしたが,こんどはそうではないので,背景の座標軸や方眼は表示しません。適当なところに線分ABを描き,その中点をとって直径ABの円を描きます。これがOがかく円です。円周上に点をとります。作図順では点Dとなるでしょう。ここで,インスペクタを開いて,点Dは名前をOにかえ,中点はMにしておきます。
Oを原点とする直交座標系(平面$${\pi}$$)をつくります。直径の端点とOを結べば直角になるので,これを座標軸とします。この平面$${\pi}$$上に点をとるには,1. でやったように,原点中心の2つの円を描いて座標を決めて点を取ります。下図では点Eがその点です。

軌跡ツールを選んで,動かす点としてO,軌跡を描く点としてEを選べばリマソンが描かれます。

B 軸が斜交している場合
平面$${\pi}$$上の2本の溝(直線)m,nが斜めに刻まれている。ここで、2直線の交点をO,交角を$${\theta}$$とする。平面$${\pi}$$上に重ねられた平面$${\tau}$$には溝に沿って動く棒(線分)AB =b が取り付けられている。
このとき、平面」が動くとき、長さ $${\dfrac{b}{\sin \theta}}$$ の棒(線分)ARについて、点Aが直線m上を動くとき,点Rは点Oで直線mに直交する直線上を動く。また、直線ABは斜傾したアステロイドの包絡線になる。

図には楕円が描かれています。この楕円と,包絡線としてのアステロイドについては,軸が直交する場合と同じように考えられますので作図も同様にできます。包絡線はインスペクタの特別な表示方法で「足跡を描く」にチェックを入れればよいのです。
問題は前半です。「長さ $${\dfrac{b}{\sin \theta}}$$ の棒(線分)AR」とはなんでしょうか。作図器の写真を見てもいまひとつわかりにくいですね。このあとの解説を読むと,「△OABの外接円の直径は正弦定理により$${\dfrac{b}{\sin \theta}}$$」と書かれているのです。作図器を見てもよくわかりませんが,Cinderellaで「外接円を描いて」作図してみましょう。
軸は直交しないので背景も必要ありません。直線ABと,斜めに交わる直線ACを作図し,AC上に点Dを取ります。Dを中心として,固定した半径の円を描き,ABとの交点Eを取り,DEを線分で結びます。
次に三角形ADEの外接円を描きます。「3点で決まる円」のツールを選んで,A,D,Eを指定します。
「2次曲線の中心を加える」ツールを選びます。外接円を描いた直後なら円が選択状態にあるのですぐに中心ができます(F)。円が選択状態になければ円をクリックして選択します。

Eを通る,この円の直径を描きます。鏡映ツールを選んで,鏡になるものとしてF,鏡に映すものとしてEを選択します。できた点Gが目的の点Rです。EとRを結び,インスペクタで点の名称を変え,補助円や点Fを非表示にしましょう。
軌跡ツールを選び,動かす点として名前を変えたBを,軌跡を描く点としてRを選びますと,Oを通る垂線が描かれます。

