
反復関数系とコッホ曲線
複素数平面上で,コッホ曲線を描きます。コッホ曲線やシェルピンスキー ・ギャスケットなどは,次節で示すように,タートルグラフィクスで描くことができ,そこでは繰り返しシステムを使って線を引いていきます。それに対し,ここでは線は引きませんので,「曲線」とは言い難いかもしれません。
インドラの真珠では2つのメビウス変換を繰り返し使ってアポロニウス・パッキングなどを描きました。それが「反復関数系」です。メビウス変換でなく,相似変換でもやりました。同じようなことをやると,コッホ曲線が描けるというわけです。
フラクタルCGコレクション(渕上季代絵著:サイエンス社)に,京都大学の畑正義氏の式が載っており,それに基づいていくつかの図を載せてあります。
$${f_0(z)=az+b \overline{z}}$$ , $${f_1(z)=c(z-1)+d(\overline{z}-1)+1}$$
この2つの関数を用い変換を繰り返します。
はじめは,$${z_0=0}$$ の1つです。これを$${f_0,f_1}$$ を適用して,$${z_{10}=f_0(z_0}$$ , $${z_{11}=f_1(z_0)}$$ の2つの点ができます。その2つの点に$${f_0,f_1}$$ をまた適用して,というのを繰り返すわけです。
リンク先を開くと次の画面になります。
上方に9つのボタンがあります。表示されていない場合は再読み込みしてください。

先ほどの式の$${a,b,c,d}$$ が点A〜Dで決まります。青い点が4つあります。ひとつは初期値の$${z_0=0}$$ で,その像はやはり 0 です。繰り返しを2回やりましたので点は4つになっています。A〜Dの4つの点はドラッグして動かすことができます。少し動かして繰り返し数を増やしてみましょう。

上のボタンには,「フラクタルCGコレクション」に掲載されているものが設定してあります。「1」がコッホ曲線です。

1回目は点AとBに重なります。2回繰り返して,点が2つ増えました。点A(原点)から始め,Bを経由してこれを結べば,コッホ曲線の基本パターンになりますね。繰り返しを増やすと次のようになります。

点が近くなって,線を引いたのとほとんど変わりません。
「インドラの真珠」の「相似変換の反復」や「反復関数系による極限集合の生成」でシェルピンスキー・ギャスケットを描いたときと同じことが起こっているわけです。
この状態から始めて,点を動かすこともできます。点Bと点Cが実軸に関して対称な場合とそうでない場合を試してみましょう。


他のメニューもやってみましょう。L-Sytem(次節)の植物の生長のような図もあります。

さて,ここまで,初期値は$${z_0=0}$$ でしたが,初期値を変えるとどうなるでしょう。インドラの真珠で実験したときは,初期値を変えても極限集合は変わりませんでした。
初期値を設定できるものが次です。
-0.2 のところに青い点があります。これが初期値です。「1」のメニューボタンを押して,コッホ曲線を表示してみましょう。
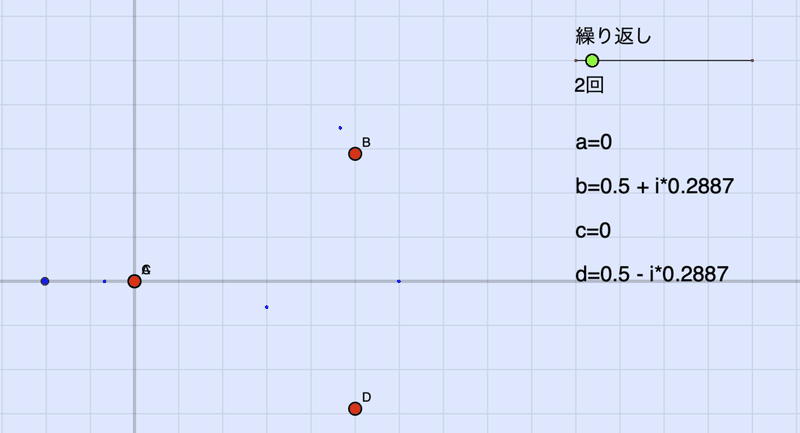
先ほどと違いますね。
繰り返し回数を増やしましょう。
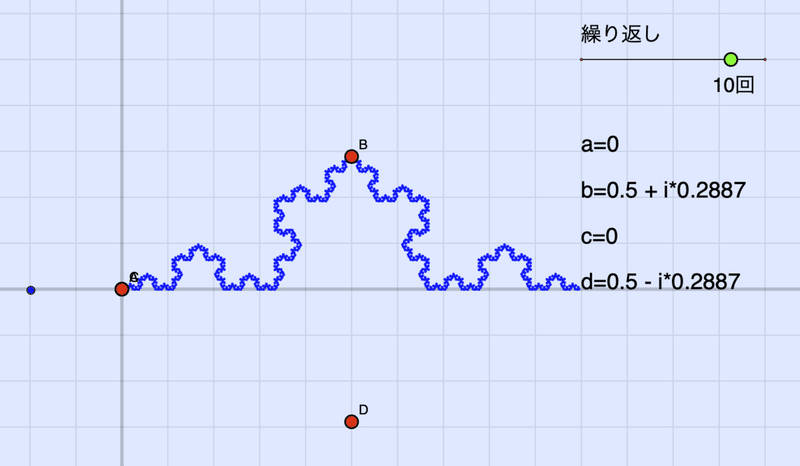
ちゃんとコッホ曲線になったようです。
初期値の青い点を動かしてみると,どこに動かしても図はかわらない(正確にはほとんど変わらない)ことがわかります。

他の設定(メニュー)でもやってみましょう。
→複素数平面とフラクタル:目次 に戻る
