
令和4年度下期 理論科目 問9 電験3種過去問
問題

考え方
この問題は、図1に示すようなインピーダンスの三角形を使って考えていく。
三角形を考える際は、大きさのみを考えていく。

解答例
電流を図2のように決める。破線で囲まれた回路の左側は、添字に$${1}$$を用いる。
右側は、添字に$${2}$$を用いる。

図2の破線で囲まれた回路の左側のインピーダンスの三角形は、図3のようになる。
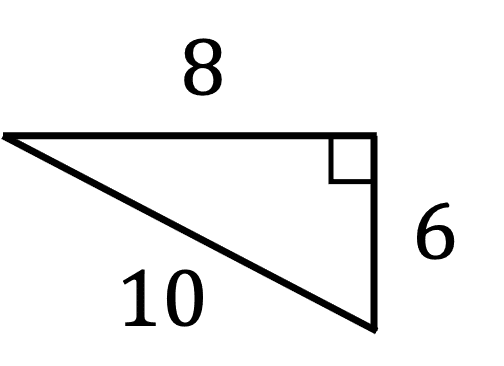
インピーダンス$${\dot{Z}_{1}}$$の大きさ$${Z_{1}}$$は、
$$
\begin{align}
Z_{1} &= \sqrt{{R_{1}}^{2}+{X_{1}}^{2}}\notag\\
&= \sqrt{8^{2}+6^{2}}\notag\\
&= 10 \,{\rm{Ω}}\tag{1}
\end{align}
$$
と求まる。
また、図3より、辺の比率は、$${Z_{1}:R_{1}:X_{1}=5:4:3}$$である。
問題文より、容量性リアクタンスで発生する電圧が$${12\,{\rm{V}}}$$であるので、インピーダンス$${Z_{1}}$$と抵抗$${R_{1}}$$で発生する電圧$${V_{Z1},V_{R1}}$$は、辺の比率を利用して、
$$
\begin{align}
V_{Z1}&=\frac{5}{3}\times12=20 \,{\rm{V}}\tag{2}\\
V_{R1}&=\frac{4}{3}\times12=16 \,{\rm{V}}\tag{3}\\
\end{align}
$$
と求まる。よって、電源の電圧$${E}$$は、
$$
E=V_{Z1}=20 \,{\rm{V}}\tag{4}
$$
となる。
図2の破線で囲まれた回路の右側のインピーダンスの三角形は、図4のようになる。

辺の比率は、図4より、$${Z_{2}:R_{2}:X_{2}=5:4:3}$$である。
インピーダンス$${Z_{2}}$$で発生する電圧$${V_{Z2}}$$は、電源電圧$${E}$$と同じであるので、
$$
V_{Z2}=E=20 \,{\rm{V}}\tag{5}
$$
となる。よって、辺の比率から抵抗$${R_{2}}$$と容量性リアクタンス$${X_{2}}$$で発生する電圧$${V_{R2},V_{X2}}$$はそれぞれ、
$$
\begin{align}
V_{R2}&=\frac{4}{5}\times20=16 \,{\rm{V}}\tag{6}\\
V_{X2}&=\frac{3}{5}\times20=12 \,{\rm{V}}\tag{7}\\
\end{align}
$$
と求まる。
破線で囲まれた回路の消費電力$${P}$$は、抵抗$${8 \,{\rm{Ω}}}$$と抵抗$${4 \,{\rm{Ω}}}$$で消費される電力の合計になる。
抵抗$${8 \,{\rm{Ω}}}$$と抵抗$${4 \,{\rm{Ω}}}$$の消費電力$${P_{8},P_{4}}$$はそれぞれ、
$$
\begin{align}
P_{8}&=\frac{{V_{R1}}^{2}}{R_{1}}=\frac{16^{2}}{8}=32 \,{\rm{W}}\tag{8}\\
P_{4}&=\frac{{V_{R2}}^{2}}{R_{2}}=\frac{16^{2}}{4}=64 \,{\rm{W}}\tag{9}\\
\end{align}
$$
となるので、破線で囲まれた回路の消費電力$${P}$$は、
$$
P=P_{8}+P_{4}=32+64=96 \,{\rm{W}}\tag{10}
$$
となる。よって、答えは(2)である。
サイト
https://sites.google.com/view/elemagscience/%E3%83%9B%E3%83%BC%E3%83%A0
