
三相誘導電動機のトルク-すべり特性
三相誘導電動機のトルク
図1に三相誘導電動機の1相分のL型等価回路を示す。
トルク$${T}$$は、機械的出力$${P_{m}}$$、角速度$${\omega}$$を用いて、
$$
T =\frac{P_{m}}{\omega} \tag{1}
$$
で求まる。
角速度$${\omega}$$は、同期角速度$${\omega_{0}}$$とすべり$${s}$$を用いて、
$$
\omega = (1-s)\omega_{0}\tag{2}
$$
と求められる。
機械的出力$${P_{m}}$$は、図1の出力抵抗$${\frac{1-s}{s}{R_{2}}^{\prime}}$$で消費される電力である。一次負荷電流$${{\dot{I}_{2}}^{\prime}}$$の大きさを$${{I_{2}}^{\prime}}$$とすれば、3相分は1相分を3倍することに注意して、
$$
\begin{align}
P_{m} &= 3\frac{1-s}{s}{R_{2}}^{\prime} {{I_{2}}^{\prime}}^{2}\tag{3}\\
\end{align}
$$
となる。
一次負荷電流の大きさ$${{I_{2}}^{\prime}}$$は、図1より
$$
\begin{align}
{I_{2}}^{\prime} &= \frac{V_{1}}{\sqrt{\left(R_{1}+\frac{{R_{2}}^{\prime}}{s}\right)^{2}+\left(x_{1}+{x_{2}}^{\prime}\right)^{2}}} \tag{4}\\
\end{align}
$$
となる。
よって、式(3)に式(4)を代入すると、
$$
\begin{align}
P_{m} &= 3\frac{1-s}{s}{R_{2}}^{\prime} {{I_{2}}^{\prime}}^{2}\notag\\
&=3\frac{1-s}{s}{R_{2}}^{\prime} {\left(\frac{V_{1}}{\sqrt{\left(R_{1}+\frac{{R_{2}}^{\prime}}{s}\right)^{2}+\left(x_{1}+{x_{2}}^{\prime}\right)^{2}}}\right)}^{2}\notag\\
&= \frac{3\frac{1-s}{s}{R_{2}}^{\prime}{V_{1}}^{2}}{\left(R_{1}+\frac{{R_{2}}^{\prime}}{s}\right)^{2}+\left(x_{1}+{x_{2}}^{\prime}\right)^{2}} \tag{5}
\end{align}
$$
を得る。
式(1)に式(2)および式(5)を代入すると、
$$
\begin{align}
&\notag\\
T &=\frac{1}{(1-s)\omega_{0}} \frac{3\frac{1-s}{s}{R_{2}}^{\prime}{V_{1}}^{2}}{\left(\left(R_{1}+\frac{{R_{2}}^{\prime}}{s}\right)^{2}+\left(x_{1}+{x_{2}}^{\prime}\right)^{2}\right)}\notag\\
&= \frac{3\frac{1}{s}{R_{2}}^{\prime}{V_{1}}^{2}}{\omega_{0}\left(\left(R_{1}+\frac{{R_{2}}^{\prime}}{s}\right)^{2}+\left(x_{1}+{x_{2}}^{\prime}\right)^{2}\right)}\tag{6}\\
\end{align}
$$
となる。式(6)において、一次相電圧の大きさ$${V_{1}}$$を一定とすると、式(6)で変化するのは、すべり$${s}$$のみである。そのため、式(6)では、$${\frac{{R_{2}}^{\prime}}{s}}$$によって、トルク$${T}$$が影響を受けることが分かる。
三相誘導電動機のトルク-すべり特性
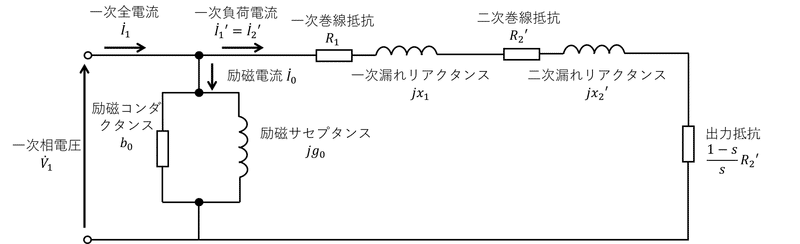
式(6)を図示すると、図2のようになる。
式(6)において、$${s=0}$$の時は、
$$
\begin{align}
&\notag\\
T &= \frac{3\frac{1}{0}{R_{2}}^{\prime}{V_{1}}^{2}}{\omega_{0}\left(\left(R_{1}+\frac{{R_{2}}^{\prime}}{0}\right)^{2}+\left(x_{1}+{x_{2}}^{\prime}\right)^{2}\right)}\notag\\
&= \frac{\infty}{\infty}\tag{7}
\end{align}
$$
となり、このままでは不定形になってしまう。
そこで、式(6)を次のように変形する。
$$
\begin{align}
&\notag\\
T &= \frac{3\frac{1}{s}{R_{2}}^{\prime}{V_{1}}^{2}}{\omega_{0}\left(\left(R_{1}+\frac{{R_{2}}^{\prime}}{s}\right)^{2}+\left(x_{1}+{x_{2}}^{\prime}\right)^{2}\right)}\notag\\
&= \frac{3{R_{2}}^{\prime}{V_{1}}^{2}}{\omega_{0}s\left(\left(R_{1}+\frac{{R_{2}}^{\prime}}{s}\right)^{2}+\left(x_{1}+{x_{2}}^{\prime}\right)^{2}\right)}\notag\\
&= \frac{3{R_{2}}^{\prime}{V_{1}}^{2}}{\omega_{0}s\left[\left(\frac{1}{s}\left(sR_{1}+{R_{2}}^{\prime}\right)\right)^{2}+\left(x_{1}+{x_{2}}^{\prime}\right)^{2}\right]}\notag\\
&= \frac{3{R_{2}}^{\prime}{V_{1}}^{2}}{\omega_{0}s\left[\frac{1}{s^{2}}\left(sR_{1}+{R_{2}}^{\prime}\right)^{2}+\left(x_{1}+{x_{2}}^{\prime}\right)^{2}\right]}\notag\\
&= \frac{3{R_{2}}^{\prime}{V_{1}}^{2}}{\omega_{0}\left(\frac{1}{s}\left(sR_{1}+{R_{2}}^{\prime}\right)^{2}+s\left(x_{1}+{x_{2}}^{\prime}\right)^{2}\right)}\tag{8}\\
\end{align}
$$
式(8)に$${s=0}$$を代入すると、
$$
\begin{align}
&\notag\\
T &= \frac{3{R_{2}}^{\prime}{V_{1}}^{2}}{\omega_{0}\left(\frac{1}{0}\left(0R_{1}+{R_{2}}^{\prime}\right)^{2}+0\left(x_{1}+{x_{2}}^{\prime}\right)^{2}\right)}\notag\\
&= \frac{3{R_{2}}^{\prime}{V_{1}}^{2}}{\omega_{0}\left(\infty\left(0+{R_{2}}^{\prime}\right)^{2}+0\right)}\notag\\
&= \frac{3{R_{2}}^{\prime}{V_{1}}^{2}}{\omega_{0}\left(\infty \times \left({R_{2}}^{\prime}\right)^{2}+0\right)}\notag\\
&= \frac{3{R_{2}}^{\prime}{V_{1}}^{2}}{\omega_{0}\left(\infty+0\right)}\notag\\
&= \frac{3{R_{2}}^{\prime}{V_{1}}^{2}}{\infty}\notag\\
&= 0 \tag{9}
\end{align}
$$
となる。
図1において$${s=0}$$のときを考えると、出力抵抗は無限大となり、開放状態と同じになる。したがって、二次電流が流れず機械的出力は$${0}$$となる。機械的出力が$${0}$$ということは、トルクも$${0}$$になる。よって、式(9)と同じ結果が得られる。
または次のように考えても同様の結論を得る。
すべりが$${0}$$ということは、回転磁界との相対速度がないため、起電力が二次巻線に誘導されず、二次側の電圧は$${0}$$である。したがって、二次電流は流れないため、機械的出力は$${0}$$となり、トルクも$${0}$$となる。
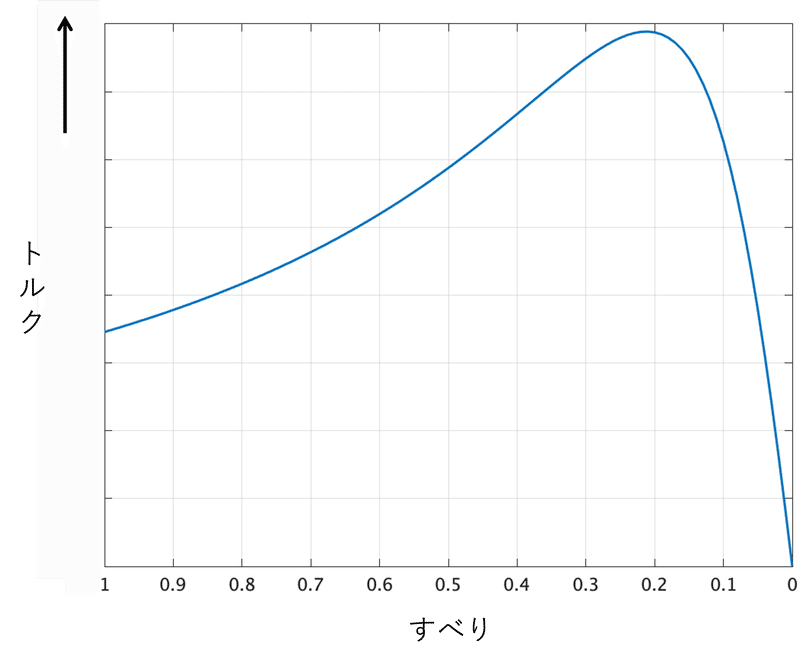
図3の赤線で囲ったすべりが小さい範囲では、トルクとすべりが比例関係とみなすことができる。
したがって、トルク$${T_{1}}$$、すべり$${s_{1}}$$で運転している状態から、トルク$${T_{2}}$$で運転したい場合、すべり$${s_{2}}$$は、次のように計算できる。
$$
\begin{align}
T_{1}:T_{2} &= s_{1}:s_{2}\notag\\
s_{2} &= \frac{T_{2}}{T_{1}}s_{1}\tag{10}
\end{align}
$$
三相誘導電動機の比例推移
巻線形誘導電動機では、二次巻線をスリップリングを通して外部に出力することができる。この二次巻線に抵抗を接続すれば、図1において二次巻線の抵抗値を変化させることができる。
式(6)において、二次巻線の抵抗は$${\frac{{R_{2}}^{\prime}}{s}}$$でトルクに影響を与えていることをみた。
今、二次巻線の各相に抵抗$${r}$$を接続した状況を考える。
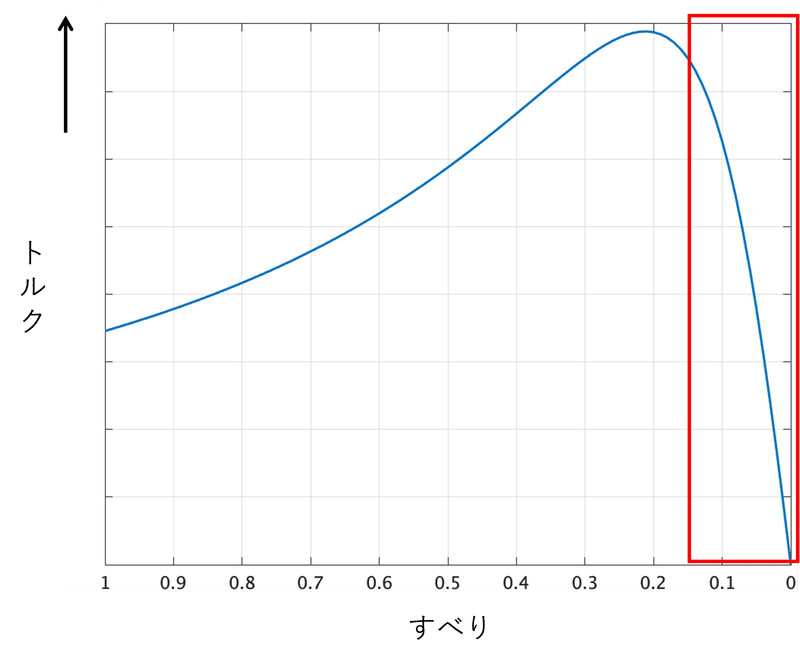
抵抗を接続した時のトルク-すべり特性は、図4のようになる。
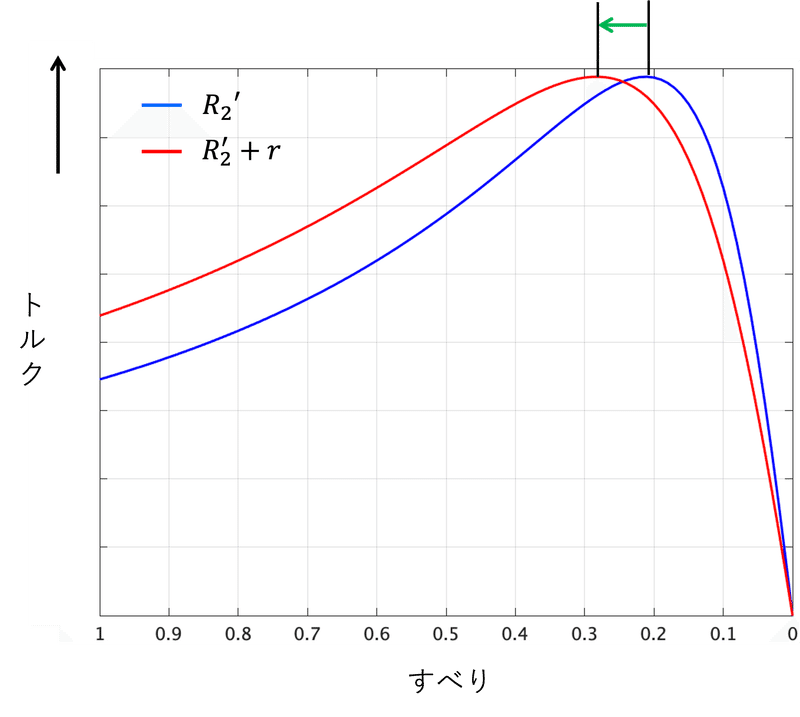
図4より、抵抗を接続すると、特性曲線がすべり$${s=1}$$の方に全体的に移動していることが分かる。また、最大トルクも移動している。
図4のすべりが小さい範囲のみに着目すると、図5のようになる。
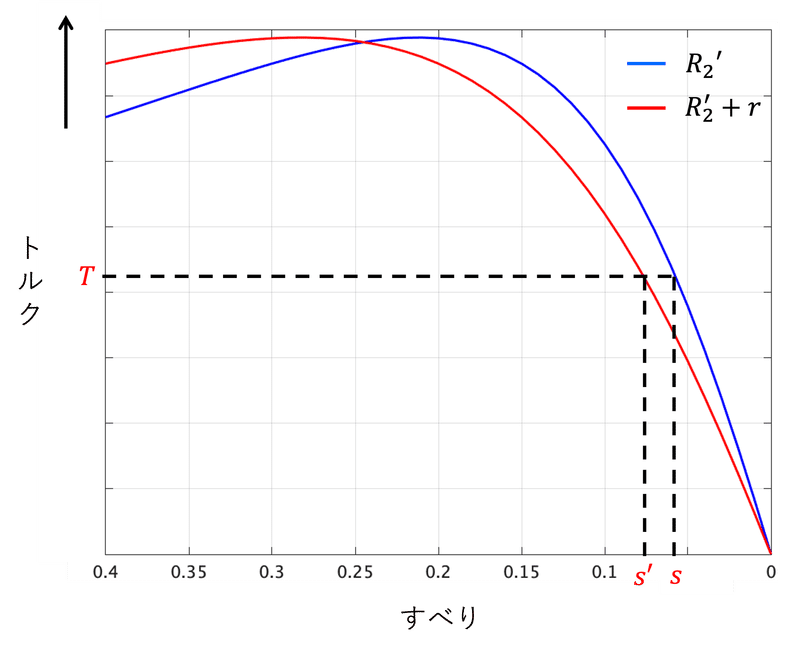
図5において、赤線で示す抵抗を接続した曲線において、すべりを$${s^{\prime}}$$とすれば、抵抗を接続した後も同じトルクを得ることができる。二次巻線の抵抗は$${\frac{{R_{2}}^{\prime}}{s}}$$でトルクに影響を与えているため、式でみると、
$$
\begin{align}
\frac{{R_{2}}^{\prime}}{s}&=\frac{{R_{2}}^{\prime}+r}{s^{\prime}}\tag{11}\\
&\notag\\
\end{align}
$$
となる。これを比例推移という。
比例推移を利用すると、図4で見たように最大トルクを停止時に持ってくることができるため、始動時のトルクを向上させることができ、始動特性の改善になる。
関連記事
等価回路でみる三相誘導電動機
https://note.com/elemag/n/n1453fa715769?sub_rt=share_pw
サイト
https://sites.google.com/view/elemagscience/%E3%83%9B%E3%83%BC%E3%83%A0
この記事が気に入ったらサポートをしてみませんか?
