変圧器の電圧変動率

2023年12月24日 18:14

この記事の読み方

電圧変動率のところでは、式展開をかなり細かく行っている。そのため、結果だけ知りたい方は、途中式の展開は読み飛ばすことをお勧めする。式展開を追っていく場合は、自身で書きながら追うことで、理解が深まると思われる。電験二種および電験一種の取得を目指す方は、式展開を追って、導出を理解しておく必要がある。特に二次試験で、導出の証明を行う問題が出された場合に、対応できないといけないため、導出の理解は必要である。

%抵抗降下と％リアクタンス降下

関連記事の%インピーダンスにおいて、定義式は、

$$
\%z = \frac{ZI}{E} \times 100 \,{\rm{[\%]}} \tag{1}
$$

$${Z}$$：インピーダンス、$${E}$$：相電圧、$${I}$$：インピーダンス$${Z}$$を流れる電流
であった。
ここで、インピーダンス$${Z}$$は、抵抗$${R}$$とリアクタンス$${X}$$を用いて、

$$
Z = \sqrt{R^{2}+X^{2}} \tag{2}
$$

となり、抵抗$${R}$$とリアクタンス$${X}$$に分解して考えることもできる。そこで、式(1)において、抵抗成分のみの場合を考えると、

$$
p = \frac{RI}{E} \times 100 \,{\rm{[\%]}} \tag{3}
$$

となる。これを%抵抗降下という。同様にリアクタンス成分のみの場合を考えると、

$$
q = \frac{XI}{E} \times 100 \,{\rm{[\%]}} \tag{4}
$$

となる。これを%リアクタンス降下という。
変圧器の場合は、電圧を二次側の定格電圧$${V_{2n}}$$(三相の場合は、相電圧)、電流を二次側の定格電流$${I_{2n}}$$、インピーダンス$${Z}$$を二次側から見たインピーダンスとするので、式(1)、式(3)および式(4)はそれぞれ、

$$
\begin{align}
\%z &= \frac{Z_{2}I_{2n}}{V_{2n}} \times 100 \,{\rm{[\%]}} \tag{5}\\
p &= \frac{\left({r_{1}}^{\prime}+r_{2}\right)I_{2n}}{V_{2n}} \times 100 = \frac{R_{2}I_{2n}}{V_{2n}} \times 100 \,{\rm{[\%]}} \tag{6}\\
q &= \frac{\left({x_{1}}^{\prime}+x_{2}\right)I_{2n}}{V_{2n}} \times 100 = \frac{X_{2}I_{2n}}{V_{2n}} \times 100 \,{\rm{[\%]}} \tag{7}\\
\end{align}
$$

$${{r_{1}}^{\prime}}$$：二次側に換算した一次巻線抵抗、$${{x_{1}}^{\prime}}$$：二次側に換算した一次漏れリアクタンス、$${r_{2}}$$：二次巻線抵抗、$${x_{2}}$$：二次漏れリアクタンス、$${R_{2}}$$：二次側から見た合成抵抗、$${X_{2}}$$：二次側から見た合成リアクタンス
となる。
注）三相の場合は、単相へ変換して考える。
式(6)は、分母分子に二次側の定格電流を掛けることで、電力から求めることができ、

$$
\begin{align}
p &= \frac{R_{2}I_{2n}}{V_{2n}} \times 100 \,{\rm{[\%]}} \notag\\
&= \frac{R_{2}I_{2n}}{V_{2n}} \times 100 \times \frac{I_{2n}}{I_{2n}}\notag\\
&= \frac{R_{2}{I_{2n}}^{2}}{V_{2n}I_{2n}} \times 100 \notag\\
&= \frac{W_{2s}}{P_{2n}}\times 100 \,{\rm{[\%]}} \tag{8}\\
\end{align}
$$

となる。$${W_{2s}}$$は、インピーダンスワットと呼ばれることもある。電験では、短絡試験の問題などで出てくることがある。なお、$${P_{2n}}$$は、変圧器の定格容量である。
また、式(2)から、%インピーダンス、%抵抗降下、%リアクタンス降下は、

$$
\begin{align}
Z_{2} &= \sqrt{{R_{2}}^{2}+{X_{2}}^{2}} \notag\\
Z_{2} \times \left(\frac{I_{2n}}{V_{2n}} \times 100 \right)&= \sqrt{{R_{2}}^{2}+{X_{2}}^{2}} \times \left(\frac{I_{2n}}{V_{2n}} \times 100 \right) \notag\\
\frac{Z_{2}I_{2n}}{V_{2n}} \times 100 &= \sqrt{\left(\frac{R_{2}I_{2n}}{V_{2n}}\times 100 \right)^{2} +\left(\frac{X_{2}I_{2n}}{V_{2n}}\times 100 \right)^{2} } \notag\\
\%z &= \sqrt{p^{2}+q^{2}} \tag{9}
\end{align}
$$

となることがわかる。

電圧変動率

電圧変動率$${\varepsilon}$$の定義式は、

$$
\varepsilon = \frac{V_{20}-V_{2n}}{V_{2n}}\times 100 \,{\rm{[\%]}} \tag{10}
$$

$${V_{20}}$$：無負荷時の二次側端子電圧、$${V_{2n}}$$：二次側の定格電圧
である。
基本的になんとか変動率という時には、

$$
\begin{align}
&\notag\\
変動率 &= \frac{その値と基準との差}{基準}\times 100 \,{\rm{[\%]}} \tag{11}
\end{align}
$$

で求める。変圧器の電圧変動率は、基準を二次側の定格電圧、もう1つの指標を無負荷時の二次側端子電圧としている。定格時より無負荷時の方が、電圧降下がない分、電圧が高いため、電圧変動率がプラスになるように無負荷時から定格時を引く必要がある。
ここからは、ベクトル図から、電圧変動率の変形版を導く。二次側からみたベクトル図を書くと図1のようになる。

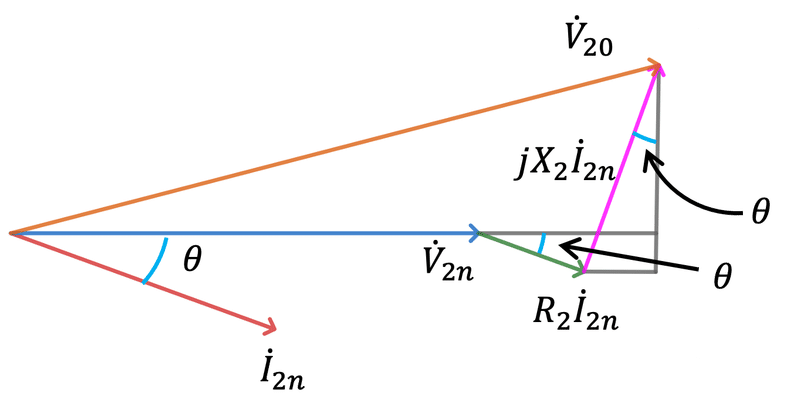
図1において、定格電圧と定格電流の位相差は$${\theta}$$としている。二次側から見た合成抵抗$${R_{2}}$$で発生する電圧$${R_{2}\dot{I}_{2n}}$$は、定格電流$${\dot{I}_{2n}}$$と同相である。二次側から見た合成リアクタンス$${jX_{2}}$$で発生する電圧$${jX_{2}\dot{I}_{2n}}$$は、電流$${\dot{I}_{2n}}$$より$${90\degree}$$位相が進む。
図1の右側を拡大したものを図2に示す。

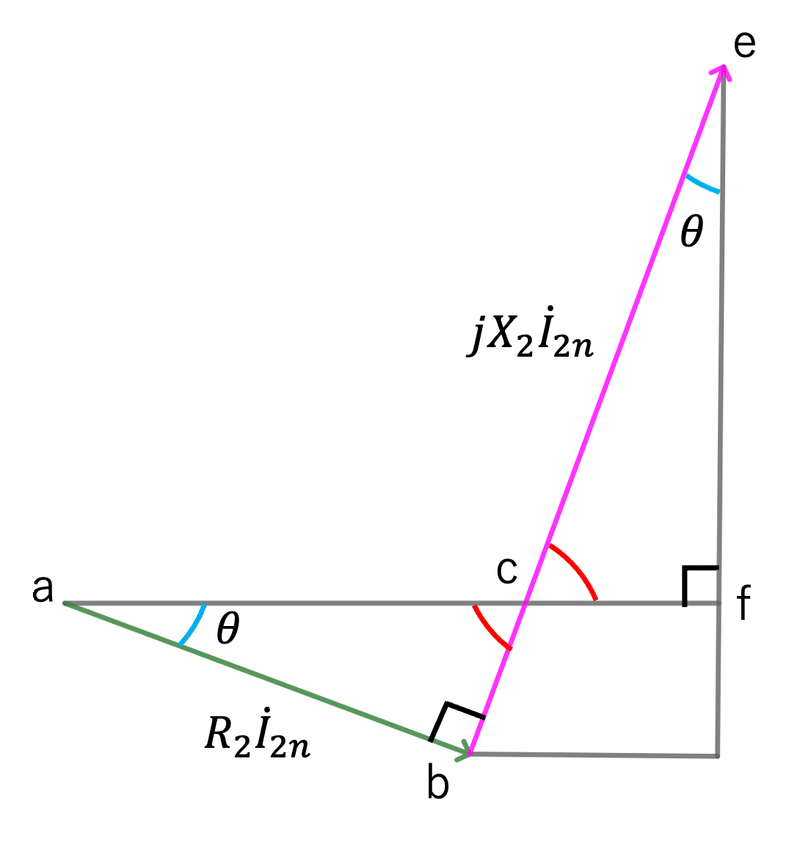
図2から、$${R_{2}\dot{I}_{2n}}$$は、定格電流$${\dot{I}_{2n}}$$と同相であるため、定格電圧$${\dot{V}_{2n}}$$を延長してできる線分afとなす角度は、$${\theta}$$となる。
三角形abcと三角形efcに着目すると、 $${\angle \rm{abc}}$$と$${\angle \rm{efc}}$$は、$${90\degree}$$であり、$${\angle \rm{bca}}$$と$${\angle \rm{fce}}$$は、対頂角であるので等しい。残った角度$${\angle \rm{cab}}$$と$${\angle \rm{cef}}$$は同じ角度となる。
よって、図1に示すような角度の関係になる。
各角度の関係がわかったところで、次に、図3に示す三角形を考える。

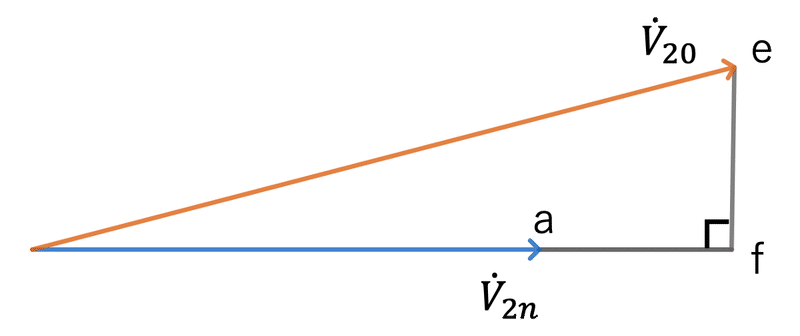
図3の三角形において、線分afと線分efの大きさがわかれば、関係式が導けそうである。線分afと線分efの大きさは、図4に示す関係から求まる。

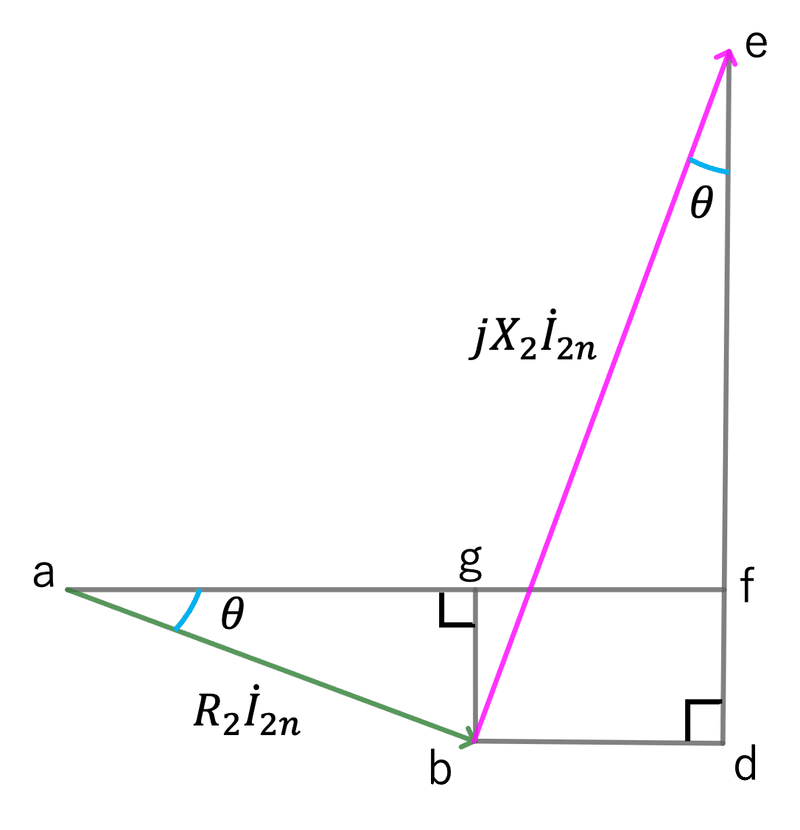
線分afは、線分agと線分gfの足し算で求まる。線分agは、定格電流の大きさを$${I_{2n}}$$とすると、

$$
line_{ag} = R_{2}I_{2n}\cos(\theta) \tag{12}
$$

と求まる。また、線分gfは線分bdと同じ長さなので、

$$
line_{gf} = X_{2}I_{2n}\sin(\theta) \tag{13}
$$

となる。よって、線分afの大きさは、

$$
\begin{align}
line_{af} &= line_{ag}+line_{gf}\notag\\
&= R_{2}I_{2n}\cos(\theta)+X_{2}I_{2n}\sin(\theta) \tag{14}
\end{align}
$$

となる。
次に、線分efは、線分edの大きさから線分fdの大きさを引いたものである。
線分edは、

$$
line_{ed} = X_{2}I_{2n}\cos(\theta)\tag{15}
$$

となる。また、線分fdは、線分gbと同じ大きさなので、

$$
line_{fd} = R_{2}I_{2n}\sin(\theta)\tag{16}
$$

となる。よって、線分efは、

$$
\begin{align}
line_{ef} &= line_{ed}-line_{fd}\notag\\
&= X_{2}I_{2n}\cos(\theta)-R_{2}I_{2n}\sin(\theta) \tag{17}
\end{align}
$$

となる。よって、図3から次式が成り立つ。

$$
\begin{align}
{V_{20}}^{2} &= \left(V_{2n} + R_{2}I_{2n}\cos(\theta)+X_{2}I_{2n}\sin(\theta) \right)^{2} \notag\\
&\quad \quad +\left(X_{2}I_{2n}\cos(\theta)-R_{2}I_{2n}\sin(\theta) \right)^{2} \tag{18}\\
\end{align}
$$

式(18)の両辺を$${{V_{2n}}^{2}}$$で割ると、

$$
\begin{align}
\frac{{V_{20}}^{2}}{{V_{2n}}^{2}} &= \left(1+\frac{R_{2}I_{2n}}{V_{2n}}\cos(\theta)+\frac{X_{2}I_{2n}}{V_{2n}}\sin(\theta) \right)^{2} \notag\\
&\quad \quad +\left(\frac{X_{2}I_{2n}}{V_{2n}}\cos(\theta)-\frac{R_{2}I_{2n}}{V_{2n}}\sin(\theta) \right)^{2} \notag\\
&= \left(1+\frac{p}{100}\cos(\theta)+\frac{q}{100}\sin(\theta) \right)^{2} \notag\\
&\quad \quad +\left(\frac{q}{100}\cos(\theta)-\frac{p}{100}\sin(\theta) \right)^{2} \tag{19}\\
\end{align}
$$

式(19)の右辺第1項を計算すると、

$$
\begin{align}
&\left(1+\frac{p}{100}\cos(\theta)+\frac{q}{100}\sin(\theta) \right)^{2}\notag\\
&= 1+\frac{p}{100}\cos(\theta)+\frac{q}{100}\sin(\theta)\notag\\
&\quad +\frac{p}{100}\cos(\theta)+\left(\frac{p}{100}\cos(\theta)\right)^{2}+\frac{p}{100}\cos(\theta)\frac{q}{100}\sin(\theta)\notag\\
&\quad +\frac{q}{100}\sin(\theta)+\frac{q}{100}\sin(\theta)\frac{p}{100}\cos(\theta)+\left(\frac{q}{100}\sin(\theta) \right)^{2}\notag\\
&= 1+\frac{2p}{100}\cos(\theta)+\frac{2q}{100}\sin(\theta) +2\frac{p}{100}\cos(\theta)\frac{q}{100}\sin(\theta)\notag\\
&\quad + \left(\frac{p}{100}\cos(\theta)\right)^{2}+ \left(\frac{q}{100}\sin(\theta) \right)^{2}\tag{20}\\
\end{align}
$$

となる。式(20)において、$${2\frac{p}{100}\cos(\theta)\frac{q}{100}\sin(\theta)}$$に

$$
2\sin(\theta)\cos(\theta) = \sin(2\theta) \tag{21}
$$

を適用すると、

$$
\begin{align}
&\left(1+\frac{p}{100}\cos(\theta)+\frac{q}{100}\sin(\theta) \right)^{2}\notag\\
&= 1+\frac{2p}{100}\cos(\theta)+\frac{2q}{100}\sin(\theta) +\frac{p}{100}\frac{q}{100}\sin(2\theta)\notag\\
&\quad + \left(\frac{p}{100}\cos(\theta)\right)^{2}+ \left(\frac{q}{100}\sin(\theta) \right)^{2}\tag{22}\\
\end{align}
$$

となる。

次に右辺第2項を計算すると、

$$
\begin{align}
&\left(\frac{q}{100}\cos(\theta)-\frac{p}{100}\sin(\theta) \right)^{2} \notag\\
&= \left(\frac{q}{100}\cos(\theta)\right)^{2}-2\frac{q}{100}\cos(\theta)\frac{p}{100}\sin(\theta)+\left(\frac{p}{100}\sin(\theta)\right)^{2}\tag{23}\\
\end{align}
$$

となる。式(23)も同様に式(21)を適用することで、

$$
\begin{align}
&\left(\frac{q}{100}\cos(\theta)-\frac{p}{100}\sin(\theta) \right)^{2} \notag\\
&= \left(\frac{q}{100}\cos(\theta)\right)^{2}-\frac{q}{100}\frac{p}{100}\sin(2\theta)+\left(\frac{p}{100}\sin(\theta)\right)^{2}\tag{24}\\
\end{align}
$$

となる。よって、右辺の足し算は式(22)と式(24)の結果から、

$$
\begin{align}
& \left(1+\frac{p}{100}\cos(\theta)+\frac{q}{100}\sin(\theta) \right)^{2} +\left(\frac{q}{100}\cos(\theta)-\frac{p}{100}\sin(\theta) \right)^{2} \notag\\
&= 1+\frac{2p}{100}\cos(\theta)+\frac{2q}{100}\sin(\theta) +\frac{p}{100}\frac{q}{100}\sin(2\theta)\notag\\
&\quad + \left(\frac{p}{100}\cos(\theta)\right)^{2}+ \left(\frac{q}{100}\sin(\theta) \right)^{2}\notag\\
&\quad +\left(\frac{q}{100}\cos(\theta)\right)^{2}-\frac{q}{100}\frac{p}{100}\sin(2\theta)+\left(\frac{p}{100}\sin(\theta)\right)^{2}\notag\\
&= 1+2\left(\frac{p}{100}\cos(\theta)+\frac{q}{100}\sin(\theta)\right)+\left(\frac{p}{100} \right)^{2}+\left(\frac{q}{100} \right)^{2}\tag{25}
\end{align}
$$

となる。なお、$${(\cos(\theta))^{2}+(\sin(\theta))^{2}=1}$$を途中に用いている。
式展開がかなり長くなったが、式(25)の結果から、式(19)は、

$$
\begin{align}
\frac{{V_{20}}^{2}}{{V_{2n}}^{2}} &=1+2\left(\frac{p}{100}\cos(\theta)+\frac{q}{100}\sin(\theta)\right)+\left(\frac{p}{100} \right)^{2}+\left(\frac{q}{100} \right)^{2}\notag\\
\frac{V_{20}}{V_{2n}} &= \sqrt{1+2\left(\frac{p}{100}\cos(\theta)+\frac{q}{100}\sin(\theta)\right)+\left(\frac{p}{100} \right)^{2}+\left(\frac{q}{100} \right)^{2}}\tag{26}\\
\end{align}
$$

となる。ここで、二項定理を用いる。

$$
(1+x)^{n} = 1+ n x+\frac{n(n-1)}{2} x^{2} + \cdots \tag{27}
$$

式(26)と式(27)を比較すると、
$${n = \frac{1}{2}}$$、$${x = 2\left(\frac{p}{100}\cos(\theta)+\frac{q}{100}\sin(\theta)\right)+\left(\frac{p}{100} \right)^{2}+\left(\frac{q}{100} \right)^{2}}$$である。
また、3次以上の項は、十分小さいとして近似すると、

$$
\begin{align}
\frac{V_{20}}{V_{2n}} &= \sqrt{1+2\left(\frac{p}{100}\cos(\theta)+\frac{q}{100}\sin(\theta)\right)+\left(\frac{p}{100} \right)^{2}+\left(\frac{q}{100} \right)^{2}}\notag\\
&\fallingdotseq 1+\frac{1}{2}\left(2\left(\frac{p}{100}\cos(\theta)+\frac{q}{100}\sin(\theta)\right)+\left(\frac{p}{100} \right)^{2}+\left(\frac{q}{100} \right)^{2} \right)\notag\\
&+\frac{\frac{1}{2}\left(\frac{1}{2}-1\right)}{2}\left(2\left(\frac{p}{100}\cos(\theta)+\frac{q}{100}\sin(\theta)\right)+\left(\frac{p}{100} \right)^{2}+\left(\frac{q}{100} \right)^{2}\right)^{2} \notag\\
&\fallingdotseq 1+\left(\frac{p}{100}\cos(\theta)+\frac{q}{100}\sin(\theta)\right)+\frac{1}{2}\left(\frac{p}{100} \right)^{2}+\frac{1}{2}\left(\frac{q}{100} \right)^{2} \notag\\
&- \frac{1}{8}\left(2\left(\frac{p}{100}\cos(\theta)+\frac{q}{100}\sin(\theta)\right)+\left(\frac{p}{100} \right)^{2}+\left(\frac{q}{100} \right)^{2}\right)^{2} \tag{28}\\
\end{align}
$$

となる。式(28)の2乗の項は、

$$
\begin{align}
&\left(2\left(\frac{p}{100}\cos(\theta)+\frac{q}{100}\sin(\theta)\right)+\left(\frac{p}{100} \right)^{2}+\left(\frac{q}{100} \right)^{2}\right)^{2} \notag\\
&= 4\left(\frac{p}{100}\cos(\theta)+\frac{q}{100}\sin(\theta)\right)^{2}\notag\\
&\quad + 2\left(\frac{p}{100}\cos(\theta)+\frac{q}{100}\sin(\theta)\right)\left(\frac{p}{100} \right)^{2}\notag\\
&\quad +2\left(\frac{p}{100}\cos(\theta)+\frac{q}{100}\sin(\theta)\right)\left(\frac{q}{100} \right)^{2}\notag\\
&\quad +2\left(\frac{p}{100}\cos(\theta)+\frac{q}{100}\sin(\theta)\right)\left(\frac{p}{100} \right)^{2}\notag\\
&\quad +\left(\frac{p}{100} \right)^{4}+\left(\frac{p}{100} \right)^{2}\left(\frac{q}{100} \right)^{2}\notag\\
&\quad + 2\left(\frac{p}{100}\cos(\theta)+ \frac{q}{100}\sin(\theta)\right)\left(\frac{q}{100} \right)^{2}\notag\\
&\quad + \left(\frac{p}{100} \right)^{2}\left(\frac{q}{100} \right)^{2}+\left(\frac{q}{100} \right)^{4}\notag\\
&= 4\left(\frac{p}{100}\cos(\theta)+\frac{q}{100}\sin(\theta)\right)^{2}\notag\\
&\quad + 4\left(\frac{p}{100}\cos(\theta)+\frac{q}{100}\sin(\theta)\right)\left(\frac{p}{100} \right)^{2}\notag\\
&\quad +4\left(\frac{p}{100}\cos(\theta)+\frac{q}{100}\sin(\theta)\right)\left(\frac{q}{100} \right)^{2}\notag\\
&\quad +\left(\frac{p}{100} \right)^{4}+2\left(\frac{p}{100} \right)^{2}\left(\frac{q}{100} \right)^{2}\notag\\
&\quad + \left(\frac{q}{100} \right)^{4}\tag{29}\\
\end{align}
$$

となる。ここで、3次以上の項は、十分小さいとして無視すると、

となる。よって、式(28)は、

となる。式(31)を展開して整理すると、

となる。式(32)において、$${\frac{1}{2}\left(\frac{p}{100} \right)^{2}}$$および$${\frac{1}{2}\left(\frac{q}{100} \right)^{2} }$$は、
$${(\cos(\theta))^{2}+(\sin(\theta))^{2}=1}$$を用いて、次のように表せる。

$$
\begin{align}
\frac{1}{2}\left(\frac{p}{100} \right)^{2} &= \frac{1}{2}\left(\frac{p}{100} \right)^{2}(\cos(\theta))^{2}+\frac{1}{2}\left(\frac{p}{100} \right)^{2}(\sin(\theta))^{2}\tag{33}\\
\frac{1}{2}\left(\frac{q}{100} \right)^{2} &= \frac{1}{2}\left(\frac{q}{100} \right)^{2}(\cos(\theta))^{2}+\frac{1}{2}\left(\frac{q}{100} \right)^{2}(\sin(\theta))^{2}\tag{34}\\
\end{align}
$$

よって、式(32)は、

$$
\begin{align}
\frac{V_{20}}{V_{2n}}
&\fallingdotseq 1+\left(\frac{p}{100}\cos(\theta)+\frac{q}{100}\sin(\theta)\right)+\frac{1}{2}\left(\frac{p}{100} \right)^{2}+\frac{1}{2}\left(\frac{q}{100} \right)^{2} \notag\\
&- \frac{1}{2}\left(\frac{p}{100}\cos(\theta)\right)^{2} - \frac{p}{100}\cos(\theta)\frac{q}{100}\sin(\theta) - \frac{1}{2}\left(\frac{q}{100}\sin(\theta)\right)^{2} \notag\\
&\fallingdotseq 1+\left(\frac{p}{100}\cos(\theta)+\frac{q}{100}\sin(\theta)\right)\notag\\
&+\frac{1}{2}\left(\frac{p}{100} \right)^{2}(\cos(\theta))^{2}+\frac{1}{2}\left(\frac{p}{100} \right)^{2}(\sin(\theta))^{2}\notag\\
&+\frac{1}{2}\left(\frac{q}{100} \right)^{2}(\cos(\theta))^{2}+\frac{1}{2}\left(\frac{q}{100} \right)^{2}(\sin(\theta))^{2} \notag\\
&- \frac{1}{2}\left(\frac{p}{100}\cos(\theta)\right)^{2} - \frac{p}{100}\cos(\theta)\frac{q}{100}\sin(\theta) - \frac{1}{2}\left(\frac{q}{100}\sin(\theta)\right)^{2} \notag\\
&\fallingdotseq 1+\left(\frac{p}{100}\cos(\theta)+\frac{q}{100}\sin(\theta)\right)\notag\\
&+\frac{1}{2}\left(\frac{p}{100}\sin(\theta)\right)^{2}- \frac{p}{100}\cos(\theta)\frac{q}{100}\sin(\theta) +\frac{1}{2}\left(\frac{q}{100}\cos(\theta)\right)^{2} \notag\\
&\fallingdotseq 1+\left(\frac{p}{100}\cos(\theta)+\frac{q}{100}\sin(\theta)\right)\notag\\
&+\frac{1}{2}\left(\left(\frac{q}{100}\cos(\theta)\right)^{2} - 2\frac{p}{100}\cos(\theta)\frac{q}{100}\sin(\theta) +\left(\frac{p}{100}\sin(\theta)\right)^{2}\right)\notag\\
&\fallingdotseq 1+\left(\frac{p}{100}\cos(\theta)+\frac{q}{100}\sin(\theta)\right)\notag\\
&\qquad \qquad +\frac{1}{2}\left(\frac{q}{100}\cos(\theta)-\frac{p}{100}\sin(\theta)\right)^{2}\tag{35}\\
\end{align}
$$

となる。電圧変動率の定義である式(10)は、

$$
\begin{align}
\varepsilon &= \frac{V_{20}-V_{2n}}{V_{2n}}\times 100 \,{\rm{[\%]}} \notag\\
&= \frac{V_{20}-V_{2n}}{V_{2n}}\times 100 \times \frac{\frac{1}{V_{2n}}}{\frac{1}{V_{2n}}}\notag\\
&= \frac{\frac{V_{20}}{V_{2n}}-1}{1}\times 100\notag\\
&\fallingdotseq \left(\left(\frac{p}{100}\cos(\theta)+\frac{q}{100}\sin(\theta)\right)+\frac{1}{2}\left(\frac{q}{100}\cos(\theta)-\frac{p}{100}\sin(\theta)\right)^{2}\right) \times 100\notag\\
&\fallingdotseq \,\,p\cos(\theta)+q\sin(\theta)+\frac{1}{200}\left(q\cos(\theta)-p\sin(\theta)\right)^{2}\,{\rm{[\%]}} \tag{36}\\
\end{align}
$$

となる。容量が小さい変圧器では、式(36)の第3項は十分小さいので、無視できて、

$$
\begin{align}
\varepsilon &\fallingdotseq p\cos(\theta)+q\sin(\theta) \,{\rm{[\%]}}\tag{37}\\
\end{align}
$$

となる。電験三種では、近似式として式(37)を用いることが多い。一方で、電験二種や電験一種では、問題文から判断して、式(36)と式(37)を使い分ける必要がある。

%インピーダンス
https://note.com/elemag/n/n88f317527145?sub_rt=share_pw

交流回路のベクトル図
https://note.com/elemag/n/n4dac09052577?sub_rt=share_pw

サイト

https://sites.google.com/view/elemagscience/%E3%83%9B%E3%83%BC%E3%83%A0

この記事が気に入ったらサポートをしてみませんか？