分圧と分流　直流回路

分圧

図1の直列回路を考える。

図1 直列回路

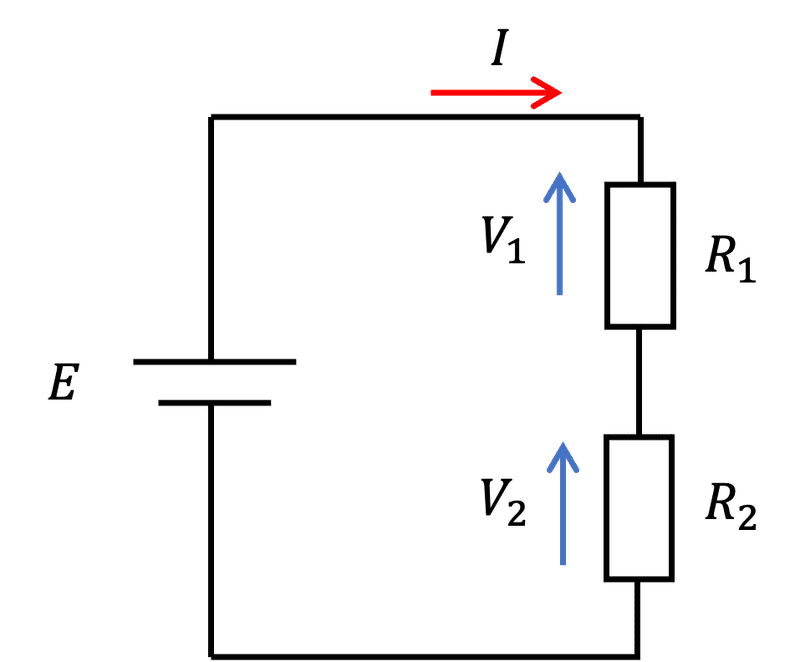
図1の回路で流れる電流$${I}$$は、

$$
I = \frac{E}{R_{1}+R_{2}}
$$

となる。

よって、電圧$${V_{1}}$$、$${V_{2}}$$はそれぞれ、

$$
\begin{align}
V_{1} &= R_{1}I\notag\\
&= R_{1}\times \frac{E}{R_{1}+R_{2}}\notag\\
&= \frac{R_{1}}{R_{1}+R_{2}}E\notag\\
&\notag\\
V_{2} &= R_{2}I\notag\\
&= R_{2}\times \frac{E}{R_{1}+R_{2}}\notag\\
&= \frac{R_{2}}{R_{1}+R_{2}}E\notag\\
\end{align}
$$

と求まる。
ここで、分母の$${R_{1}+R_{2}}$$は、直列回路の合成抵抗なので、$${R}$$とすれば、

$$
\begin{align}
V_{1} &= \frac{R_{1}}{R_{1}+R_{2}}E\notag\\
&= \frac{R_{1}}{R}E\notag\\
&\notag\\
V_{2} &= \frac{R_{2}}{R_{1}+R_{2}}E\notag\\
&= \frac{R_{2}}{R}E\notag\\
\end{align}
$$

となる。

一般的に$${n}$$個の場合の$${k}$$番目の抵抗に発生する電圧$${V_{k}}$$は、

$$
\begin{align}
V_{k} &= \frac{R_{k}}{R_{1}+R_{2}+\cdots+R_{n}}E\notag\\
&= \frac{R_{k}}{R}E\notag\\
\end{align}
$$

となる。
また、全電圧$${E}$$は、

$$
\begin{align}
E &= \sum_{i=1}^{n}\frac{R_{i}}{R}E\notag\\
\end{align}
$$

で求まる。

分流

図2に示す並列回路を考える。

図2 並列回路

図2の回路の合成抵抗を$${R}$$とすれば、電源電圧$${E}$$は、

$$
\begin{align}
E &= RI\notag\\
\end{align}
$$

となる。
よって、各抵抗に流れる電流は、

$$
\begin{align}
I_{1} &= \frac{E}{R_{1}}\notag\\
&=  \frac{R}{R_{1}}I\notag\\
&\notag\\
I_{2} &= \frac{E}{R_{2}}\notag\\
&=  \frac{R}{R_{2}}I\notag\\
\end{align}
$$

となる。

並列回路の場合、コンダクタンスを用いることで計算が簡単になる場合がある。
コンダクタンス$${G}$$は抵抗$${R}$$の逆数であるため、

$$
G =\frac{1}{R}
$$

の関係がある。
また、並列回路の合成抵抗は、

$$
\begin{align}
\frac{1}{R} &=\frac{1}{R_{1}}+\frac{1}{R_{2}}\notag\\
G&=  G_{1}+G_{2}\notag\\
\end{align}
$$

となり、コンダクタンスで考える場合には、和で求めることができる。
よって、各抵抗に流れる電流をコンダクタンスで表すと、電源電圧$${E}$$は、

$$
\begin{align}
E &= \frac{I}{G}\notag\\
\end{align}
$$

となるので、

$$
\begin{align}
I_{1} &= EG_{1}\notag\\
&=  \frac{G_{1}}{G}I\notag\\
&\notag\\
I_{2} &= EG_{2}\notag\\
&=  \frac{G_{2}}{G}I\notag\\
\end{align}
$$

となる。

関連記事

抵抗の合成　電気回路
https://note.com/elemag/n/n80cef07bc097?sub_rt=share_pw

サイト

https://sites.google.com/view/elemagscience/%E3%83%9B%E3%83%BC%E3%83%A0