
インダクタンス(制動巻線考慮なし) 同期機
同期機の固定子巻線
同期の固定子巻線は、図1に示すように$${\frac{2}{3}\pi}$$ずつずれた配置となっているものとして考えられる。
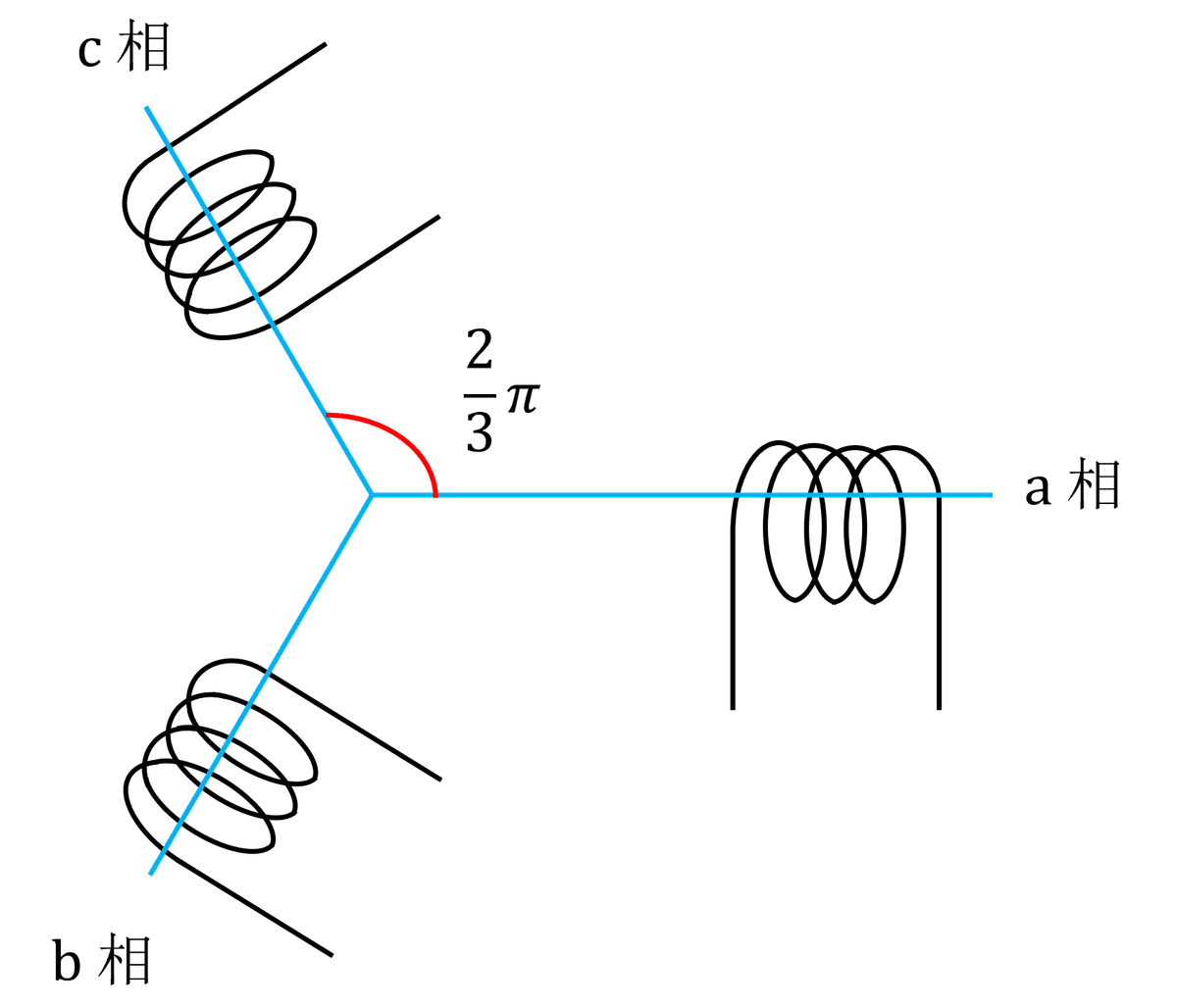
また、回転子の軸を図2のように定義する。

以降の図では、巻線の絵は省略し、線で表現する。
インダクタンス
固定子巻線と回転子巻線はそれぞれ自己インダクタンスをもち、各巻線に電流が流れた場合、相互インダクタンスを持つ。
自己インダクタンス$${L}$$は、コイルを貫く磁束$${\phi}$$とコイルに流れる電流$${I}$$を用いて、
$$
\phi = LI \tag{1}
$$
で求まる。
自己インダクタンス
$${\rm{a}}$$相の自己インダクタンスを考える。
$${\rm{a}}$$相の巻線に電流$${I_{\rm{a}}}$$を流した場合、コイルを貫く磁束$${\phi_{\rm{a}}}$$が求まれば、式(1)より$${\rm{a}}$$相の自己インダクタンスが分かる。
$${\rm{a}}$$相の巻線と回転子軸が図3に示すような関係の場合を考える。

磁気回路の考え方をすると、磁束$${\phi}$$は磁気抵抗$${R_{\rm{m}}}$$と起磁力$${F}$$を用いて、
$$
\phi = \frac{F}{R_{\rm{m}}}\tag{2}
$$
で求まる。
$${\rm{a}}$$相巻線の起磁力$${F_{\rm{a}}}$$は、巻数を$${N}$$とすれば、
$$
F_{\rm{a}}=Ni_{\rm{a}}
$$
で求まる。
この起磁力を図4のように回転子軸方向($${\rm{d}}$$軸)とこれに直角な方向($${\rm{q}}$$軸)の成分に分解する。

$$
\begin{align}
F_{\rm{d}} &= Ni_{\rm{a}}\cos(\theta)\notag\\
F_{\rm{q}} &= Ni_{\rm{a}}\sin(\theta)\notag\\
\end{align}
$$
したがって、$${\rm{d}}$$軸および$${\rm{q}}$$軸の磁束は、式(2)より
$$
\begin{align}
\phi_{\rm{d}} &= \frac{F_{\rm{d}}}{R_{\rm{d}}}\notag\\
&= \frac{Ni_{\rm{a}}}{R_{\rm{d}}}\cos(\theta)\tag{3}\\
&\notag\\
\phi_{\rm{q}} &= \frac{F_{\rm{q}}}{R_{\rm{q}}}\notag\\
&= \frac{Ni_{\rm{a}}}{R_{\rm{q}}}\sin(\theta)\tag{4}\\
\end{align}
$$
となる。
$${\rm{a}}$$相巻線を貫く磁束は、図5に示すような磁束となる。

図5より$${\rm{a}}$$相巻線を貫く磁束は、巻線の巻数を$${N}$$とすれば、
$$
\begin{align}
\phi_{\rm{a}} &=N\left(( \phi_{\rm{d}}\cos(\theta)+\phi_{\rm{q}}\cos\left(\frac{\pi}{2}-\theta\right)\right)\notag\\
&=N(\phi_{\rm{d}}\cos(\theta)+\phi_{\rm{q}}\sin(\theta))\tag{5}\\
\end{align}
$$
と求まる。
式(5)に式(3)および(4)の結果を代入すれば、
$$
\begin{align}
\phi_{\rm{a}} &= N(\phi_{\rm{d}}\cos(\theta)+\phi_{\rm{q}}\sin(\theta))\notag\\
&= N\left(\frac{Ni_{\rm{a}}}{R_{\rm{d}}}(\cos(\theta))^{2}+ \frac{Ni_{\rm{a}}}{R_{\rm{q}}}(\sin(\theta))^{2}\right)\tag{6}\\
\end{align}
$$
となる。ここで、
$$
\begin{align}
&\notag\\
\cos(2\theta) &= 2(\cos(\theta))^{2}-1=1-2(\sin(\theta))^{2}\notag\\
&\notag\\
(\cos(\theta))^{2} &=\frac{1}{2}(1+\cos(2\theta) )\notag\\
&\notag\\
(\sin(\theta))^{2} &=\frac{1}{2}(1-\cos(2\theta) )\notag\\
\end{align}
$$
なので、式(6)は
$$
\begin{align}
\phi_{\rm{a}} &= N\left(\frac{Ni_{\rm{a}}}{R_{\rm{d}}}(\cos(\theta))^{2}+ \frac{Ni_{\rm{a}}}{R_{\rm{q}}}(\sin(\theta))^{2}\right)\notag\\
&\notag\\
&=\frac{N^{2}i_{\rm{a}}}{2R_{\rm{d}}}(1+\cos(2\theta))+ \frac{N^{2}i_{\rm{a}}}{2R_{\rm{q}}}(1-\cos(2\theta))\notag\\
&\notag\\
&= \frac{N^{2}i_{\rm{a}}}{2R_{\rm{d}}}+\frac{N^{2}i_{\rm{a}}}{2R_{\rm{d}}}\cos(2\theta)+ \frac{N^{2}i_{\rm{a}}}{2R_{\rm{q}}}-\frac{N^{2}i_{\rm{a}}}{2R_{\rm{q}}}\cos(2\theta)\notag\\
&\notag\\
&= \frac{N^{2}i_{\rm{a}}}{2}\left(\frac{1}{R_{\rm{d}}}+\frac{1}{R_{\rm{q}}}\right)+\frac{N^{2}i_{\rm{a}}}{2}\left(\frac{1}{R_{\rm{d}}}-\frac{1}{R_{\rm{q}}}\right)\cos(2\theta)\notag\\
&\notag\\
&= \left[\frac{N^{2}}{2}\left(\frac{1}{R_{\rm{d}}}+\frac{1}{R_{\rm{q}}}\right)+\frac{N^{2}}{2}\left(\frac{1}{R_{\rm{d}}}-\frac{1}{R_{\rm{q}}}\right)\cos(2\theta)\right]i_{\rm{a}}\notag\\
\end{align}
$$
となる。
よって、$${\rm{a}}$$相巻線の自己インダクタンス$${L_{\rm{aa}}}$$は、式(1)より、
$$
\begin{align}
L_{\rm{aa}} &= \frac{\phi_{\rm{a}}}{i_{\rm{a}}}\notag\\
&=\left[\frac{N^{2}}{2}\left(\frac{1}{R_{\rm{d}}}+\frac{1}{R_{\rm{q}}}\right)+\frac{N^{2}}{2}\left(\frac{1}{R_{\rm{d}}}-\frac{1}{R_{\rm{q}}}\right)\cos(2\theta)\right]i_{\rm{a}}\times \frac{1}{i_{\rm{a}}}\notag\\
&\notag\\
&=\frac{N^{2}}{2}\left(\frac{1}{R_{\rm{d}}}+\frac{1}{R_{\rm{q}}}\right)+\frac{N^{2}}{2}\left(\frac{1}{R_{\rm{d}}}-\frac{1}{R_{\rm{q}}}\right)\cos(2\theta)\notag\\
\end{align}
$$
となる。
ここで、
$$
\begin{align}
&\notag\\
L_{1} &=\frac{N^{2}}{2}\left(\frac{1}{R_{\rm{d}}}+\frac{1}{R_{\rm{q}}}\right)\notag\\
\notag\\
L_{2} &=\frac{N^{2}}{2}\left(\frac{1}{R_{\rm{d}}}-\frac{1}{R_{\rm{q}}}\right)\notag\\
\end{align}
$$
とすれば、
$$
\begin{align}
&\notag\\
L_{\rm{aa}} &= \frac{N^{2}}{2}\left(\frac{1}{R_{\rm{d}}}+\frac{1}{R_{\rm{q}}}\right)+\frac{N^{2}}{2}\left(\frac{1}{R_{\rm{d}}}-\frac{1}{R_{\rm{q}}}\right)\cos(2\theta)\notag\\
&\notag\\
&= L_{1}+L_{2}\cos(2\theta)\notag\\
\end{align}
$$
となる。
a相とb相の相互インダクタンス
$${\rm{a}}$$相巻線を流れる電流$${i_{\rm{a}}}$$相によって、$${\rm{b}}$$相を貫く磁束を考える。
$${\phi_{\rm{db}}}$$は図6に示すような関係がある。

$$
\begin{align}
\phi_{\rm{db}} &= \phi_{\rm{d}}\cos \left(\theta-\frac{2}{3}\pi \right)\notag\\
&= \phi_{\rm{d}}\cos \left(\frac{2}{3}\pi - \theta\right)\tag{7}\\
\end{align}
$$
$${\phi_{\rm{qb}}}$$は図7に示すような関係がある。

$$
\begin{align}
\phi_{\rm{qb}} &= \phi_{\rm{q}}\cos \left(\theta-\frac{2}{3}\pi +\frac{\pi}{2} \right)\notag\\
&= \phi_{\rm{q}}\cos \left( \theta- \frac{1}{6}\pi \right)\tag{8}\\
\end{align}
$$
よって、$${\rm{a}}$$相巻線を流れる電流$${i_{\rm{a}}}$$相によって、$${\rm{b}}$$相を貫く磁束は、$${\phi_{\rm{qb}}}$$が逆向きであることを考慮すると、式(7)および式(8)より、
$$
\begin{align}
\phi_{\rm{b}} &= N\left(\phi_{\rm{db}}-\phi_{\rm{qb}}\right)\notag\\
&= N\left(\phi_{\rm{d}}\cos \left(\frac{2}{3}\pi -\theta \right)-\phi_{\rm{q}}\cos \left(\theta - \frac{\pi}{6}\right)\right)\tag{9}\\
\end{align}
$$
で求まる。
式(3)と式(4)を代入して、
$$
\begin{align}
\phi_{\rm{b}} &= N\left( \frac{Ni_{\rm{a}}}{R_{\rm{d}}}\cos(\theta)\cos \left(\frac{2}{3}\pi -\theta \right)- \frac{Ni_{\rm{a}}}{R_{\rm{q}}}\sin(\theta)\cos \left(\theta - \frac{\pi}{6}\right)\right)\notag\\
&\notag\\
&=\frac{N^{2}i_{\rm{a}}}{R_{\rm{d}}}\cos(\theta)\cos \left(\frac{2}{3}\pi -\theta \right)- \frac{N^{2}i_{\rm{a}}}{R_{\rm{q}}}\sin(\theta)\cos \left(\theta - \frac{\pi}{6}\right)\notag\\
\end{align}
$$
ここで、$${\cos \left(\frac{2}{3}\pi -\theta \right)}$$と$${\cos \left(\theta - \frac{\pi}{6}\right)}$$を加法定理を用いて書き換えると、
$$
\begin{align}
\cos \left(\frac{2}{3}\pi -\theta \right)&= \cos\left(\frac{2}{3}\pi \right) \cos(\theta) + \sin\left(\frac{2}{3}\pi \right) \sin(\theta) \notag\\
&= -\frac{1}{2} \cos(\theta) + \frac{\sqrt{3}}{2} \sin(\theta) \notag\\
\end{align}
$$
$$
\begin{align}
\cos \left(\theta - \frac{\pi}{6}\right)&= \cos(\theta)\cos\left( \frac{\pi}{6} \right) +\sin(\theta) \sin\left(\frac{\pi}{6} \right) \notag\\
&= \frac{\sqrt{3}}{2} \cos(\theta) + \frac{1}{2} \sin(\theta) \notag\\
\end{align}
$$
となる。これを代入すると、
$$
\begin{align}
\phi_{\rm{b}} &=\frac{N^{2}i_{\rm{a}}}{R_{\rm{d}}}\cos(\theta)\left( -\frac{1}{2} \cos(\theta) + \frac{\sqrt{3}}{2} \sin(\theta) \right)\notag\\
&\qquad \qquad \qquad- \frac{N^{2}i_{\rm{a}}}{R_{\rm{q}}}\sin(\theta)\left(\frac{\sqrt{3}}{2} \cos(\theta) + \frac{1}{2} \sin(\theta)\right)\notag\\
&\notag\\
&=-\frac{1}{2}\frac{N^{2}i_{\rm{a}}}{R_{\rm{d}}}(\cos(\theta))^{2} +\frac{\sqrt{3}}{2}\frac{N^{2}i_{\rm{a}}}{R_{\rm{d}}}\cos(\theta)\sin(\theta) \notag\\
&\qquad \qquad \qquad-\frac{\sqrt{3}}{2} \frac{N^{2}i_{\rm{a}}}{R_{\rm{q}}}\cos(\theta)\sin(\theta) - \frac{1}{2}\frac{N^{2}i_{\rm{a}}}{R_{\rm{q}}}(\sin(\theta))^{2}\notag\\
\end{align}
$$
と求まる。
ここで2倍角の式より、
$$
\begin{align}
\sin(2\theta) &= 2\cos(\theta)\sin(\theta) \notag\\
\cos(\theta)\sin(\theta) &= \frac{\sin(2\theta)}{2} \tag{10}\\
\end{align}
$$
$$
\begin{align}
\cos(2\theta) &= 2(\cos(\theta))^{2}−1 \notag\\
(\cos(\theta))^{2} &= \frac{1}{2}\left(\cos(2\theta)+1\right) \tag{11}\\
\end{align}
$$
$$
\begin{align}
\cos(2\theta) &= 1-2(\sin(\theta))^{2} \notag\\
(\sin(\theta))^{2} &= \frac{1}{2}\left(1-\cos(2\theta)\right) \tag{12}\\
\end{align}
$$
となるので、これらを用いると、
$$
\begin{align}
\phi_{\rm{b}} &=-\frac{1}{2}\frac{N^{2}i_{\rm{a}}}{R_{\rm{d}}}\frac{1}{2}\left(\cos(2\theta)+1\right) +\frac{\sqrt{3}}{2}\frac{N^{2}i_{\rm{a}}}{R_{\rm{d}}}\frac{\sin(2\theta)}{2} \notag\\
&\qquad \qquad \qquad-\frac{\sqrt{3}}{2} \frac{N^{2}i_{\rm{a}}}{R_{\rm{q}}}\frac{\sin(2\theta)}{2} - \frac{1}{2}\frac{N^{2}i_{\rm{a}}}{R_{\rm{q}}}\frac{1}{2}\left(1-\cos(2\theta)\right)\notag\\
&\notag\\
&= -\frac{1}{2}\frac{1}{2}\frac{N^{2}i_{\rm{a}}}{R_{\rm{d}}}\cos(2\theta)-\frac{1}{2}\frac{1}{2}\frac{N^{2}i_{\rm{a}}}{R_{\rm{d}}} +\frac{1}{2}\frac{\sqrt{3}}{2}\frac{N^{2}i_{\rm{a}}}{R_{\rm{d}}}\sin(2\theta)\notag\\
&\qquad \qquad -\frac{1}{2}\frac{\sqrt{3}}{2} \frac{N^{2}i_{\rm{a}}}{R_{\rm{q}}}\sin(2\theta) -\frac{1}{2} \frac{1}{2}\frac{N^{2}i_{\rm{a}}}{R_{\rm{q}}} + \frac{1}{2} \frac{1}{2}\frac{N^{2}i_{\rm{a}}}{R_{\rm{q}}}\cos(2\theta)\notag\\
&\notag\\
&= -\frac{N^{2}i_{\rm{a}}}{4}\left(\frac{1}{R_{\rm{d}}}+\frac{1}{R_{\rm{q}}}\right) -\frac{1}{2}\cos(2\theta)\frac{N^{2}i_{\rm{a}}}{2}\left(\frac{1}{R_{\rm{d}}}-\frac{1}{R_{\rm{q}}}\right)\notag\\
&\qquad \qquad \qquad \qquad+\frac{\sqrt{3}}{2}\sin(2\theta)\frac{N^{2}i_{\rm{a}}}{2}\left(\frac{1}{R_{\rm{d}}}-\frac{1}{R_{\rm{q}}}\right)\notag\\
&= -\frac{N^{2}i_{\rm{a}}}{4}\left(\frac{1}{R_{\rm{d}}}+\frac{1}{R_{\rm{q}}}\right) \notag\\
&\qquad \qquad \qquad \qquad +\left(-\frac{1}{2}\cos(2\theta)+\frac{\sqrt{3}}{2}\sin(2\theta) \right)\frac{N^{2}i_{\rm{a}}}{2}\left(\frac{1}{R_{\rm{d}}}-\frac{1}{R_{\rm{q}}}\right)\notag\\
\end{align}
$$
となる。
ここで、$${\cos \left(2\theta - \frac{2}{3}\pi \right)}$$を計算すると、
$$
\begin{align}
\cos\left(2\theta - \frac{2}{3}\pi \right) &= \cos(2\theta)\cos\left(\frac{2}{3}\pi \right)+\sin(2\theta)\sin\left(\frac{2}{3}\pi \right) \notag\\
&= -\frac{1}{2}\cos(2\theta)+\frac{\sqrt{3}}{2}\sin(2\theta)\notag\\
\end{align}
$$
なので、これを用いて、
$$
\begin{align}
\phi_{\rm{b}} &= -\frac{N^{2}i_{\rm{a}}}{4}\left(\frac{1}{R_{\rm{d}}}+\frac{1}{R_{\rm{q}}}\right) +\cos\left(2\theta - \frac{2}{3}\pi \right)\frac{N^{2}i_{\rm{a}}}{2}\left(\frac{1}{R_{\rm{d}}}-\frac{1}{R_{\rm{q}}}\right)\notag\\
&\notag\\
&= -\frac{N^{2}i_{\rm{a}}}{4}\left(\frac{1}{R_{\rm{d}}}+\frac{1}{R_{\rm{q}}}\right) +\frac{N^{2}i_{\rm{a}}}{2}\left(\frac{1}{R_{\rm{d}}}-\frac{1}{R_{\rm{q}}}\right)\cos\left(2\theta - \frac{2}{3}\pi \right)\notag\\
\end{align}
$$
となる。
よって、$${\rm{a}}$$相と$${\rm{b}}$$相の相互インダクタンス$${L_{\rm{ab}}}$$ は、
$$
\begin{align}
L_{\rm{ab}} &= \frac{\phi_{\rm{b}}}{i_{\rm{a}}}\notag\\
&\notag\\
&=-\frac{N^{2}}{4}\left(\frac{1}{R_{\rm{d}}}+\frac{1}{R_{\rm{q}}}\right) +\frac{N^{2}}{2}\left(\frac{1}{R_{\rm{d}}}-\frac{1}{R_{\rm{q}}}\right)\cos\left(2\theta - \frac{2}{3}\pi \right) \notag\\
\end{align}
$$
となる。
ここで、
$$
\begin{align}
&\notag\\
L_{3} &=\frac{N^{2}}{4}\left(\frac{1}{R_{\rm{d}}}+\frac{1}{R_{\rm{q}}}\right)\notag\\
\end{align}
$$
とすれば、
$$
\begin{align}
L_{\rm{ab}} &=-L_{3} +L_{2}\cos\left(2\theta - \frac{2}{3}\pi \right) \notag\\
\end{align}
$$
となる。
また、相互インダクタンスは、どちらも等しいので、
$$
L_{\rm{ba}} = L_{\rm{ab}}
$$
となる。
a相とc相の相互インダクタンス
$${\rm{a}}$$相巻線を流れる電流$${i_{\rm{a}}}$$相によって、$${\rm{c}}$$相を貫く磁束を考える。
$${\phi_{\rm{dc}}}$$は図8に示すような関係がある。

$$
\begin{align}
\phi_{\rm{dc}} &= \phi_{\rm{d}}\cos \left(\pi-\left(\theta+\frac{2}{3}\pi \right) \right)\notag\\
&= \phi_{\rm{d}}\cos \left(\frac{1}{3}\pi -\theta \right)\tag{13}\\
\end{align}
$$
$${\phi_{\rm{qc}}}$$は図9に示すような関係がある。

$$
\begin{align}
\phi_{\rm{qc}} &= \phi_{\rm{q}}\cos \left(\frac{2}{3}\pi -\left(\frac{1}{2}\pi-\theta\right) \right)\notag\\
&= \phi_{\rm{q}}\cos \left( \frac{1}{6}\pi + \theta\right)\tag{14}\\
\end{align}
$$
よって、$${\rm{a}}$$相巻線を流れる電流$${i_{\rm{a}}}$$相によって、$${\rm{c}}$$相を貫く磁束は、$${\phi_{\rm{dc}}}$$が逆向きであることを考慮すると、式(13)および式(14)より、
$$
\begin{align}
\phi_{\rm{c}} &= N\left(-\phi_{\rm{d}}\cos \left(\frac{\pi}{3} -\theta \right)+\phi_{\rm{q}}\cos \left( \frac{\pi}{6}+\theta \right) \right)\notag\\
\end{align}
$$
となる。
式(3)と式(4)を代入すると、
$$
\begin{align}
\phi_{\rm{c}} &= N\left(-\frac{Ni_{\rm{a}}}{R_{\rm{d}}}\cos(\theta)\cos \left(\frac{\pi}{3} -\theta \right)+\frac{Ni_{\rm{a}}}{R_{\rm{q}}}\sin(\theta)\cos \left( \frac{\pi}{6}+\theta \right)\right)\notag\\
&= -\frac{N^{2}i_{\rm{a}}}{R_{\rm{d}}}\cos(\theta)\cos \left(\frac{\pi}{3} -\theta \right)+\frac{N^{2}i_{\rm{a}}}{R_{\rm{q}}}\sin(\theta)\cos \left( \frac{\pi}{6}+\theta \right)\notag\\
\end{align}
$$
と求まる。
ここで、$${\cos \left(\frac{\pi}{3} -\theta \right)}$$と$${\cos \left( \frac{\pi}{6}+\theta \right)}$$を加法定理を用いて書き換えると、
$$
\begin{align}
\cos \left(\frac{\pi}{3} -\theta \right)&= \cos\left(\frac{\pi}{3} \right) \cos(\theta) + \sin\left(\frac{\pi}{3} \right) \sin(\theta) \notag\\
&= \frac{1}{2} \cos(\theta) + \frac{\sqrt{3}}{2} \sin(\theta) \notag\\
\end{align}
$$
$$
\begin{align}
\cos \left( \frac{\pi}{6}+\theta \right)&= \cos\left( \frac{\pi}{6} \right)\cos(\theta) - \sin\left( \frac{\pi}{6} \right)\sin(\theta) \notag\\
&= \frac{\sqrt{3}}{2} \cos(\theta) - \frac{1}{2} \sin(\theta) \notag\\
\end{align}
$$
となる。これを代入すると、
$$
\begin{align}
\phi_{\rm{c}} &=-\frac{N^{2}i_{\rm{a}}}{R_{\rm{d}}}\cos(\theta)\left( \frac{1}{2} \cos(\theta) + \frac{\sqrt{3}}{2} \sin(\theta) \right)\notag\\
&\qquad \qquad \qquad+ \frac{N^{2}i_{\rm{a}}}{R_{\rm{q}}}\sin(\theta)\left( \frac{\sqrt{3}}{2} \cos(\theta) - \frac{1}{2} \sin(\theta)\right)\notag\\
&\notag\\
&=-\frac{1}{2}\frac{N^{2}i_{\rm{a}}}{R_{\rm{d}}}(\cos(\theta))^{2} -\frac{\sqrt{3}}{2}\frac{N^{2}i_{\rm{a}}}{R_{\rm{d}}}\cos(\theta)\sin(\theta) \notag\\
&\qquad \qquad \qquad+\frac{\sqrt{3}}{2} \frac{N^{2}i_{\rm{a}}}{R_{\rm{q}}}\cos(\theta)\sin(\theta) - \frac{1}{2}\frac{N^{2}i_{\rm{a}}}{R_{\rm{q}}}(\sin(\theta))^{2}\notag\\
\end{align}
$$
となる。
ここで式(10)から式(12)の関係を用いると、
$$
\begin{align}
\phi_{\rm{c}} &=-\frac{1}{2}\frac{N^{2}i_{\rm{a}}}{R_{\rm{d}}}\frac{1}{2}\left(\cos(2\theta)+1\right) -\frac{\sqrt{3}}{2}\frac{N^{2}i_{\rm{a}}}{R_{\rm{d}}}\frac{\sin(2\theta)}{2}\notag\\
&\qquad \qquad \qquad+\frac{\sqrt{3}}{2} \frac{N^{2}i_{\rm{a}}}{R_{\rm{q}}}\frac{\sin(2\theta)}{2} - \frac{1}{2}\frac{N^{2}i_{\rm{a}}}{R_{\rm{q}}}\frac{1}{2}\left(1-\cos(2\theta)\right)\notag\\
&\notag\\
&= -\frac{1}{2}\frac{1}{2}\frac{N^{2}i_{\rm{a}}}{R_{\rm{d}}}\cos(2\theta)-\frac{1}{2}\frac{1}{2}\frac{N^{2}i_{\rm{a}}}{R_{\rm{d}}} -\frac{\sqrt{3}}{2}\frac{N^{2}i_{\rm{a}}}{R_{\rm{d}}}\frac{\sin(2\theta)}{2}\notag\\
&\qquad \qquad \qquad +\frac{\sqrt{3}}{2} \frac{N^{2}i_{\rm{a}}}{R_{\rm{q}}}\frac{\sin(2\theta)}{2} - \frac{1}{2}\frac{1}{2}\frac{N^{2}i_{\rm{a}}}{R_{\rm{q}}}+ \frac{1}{2}\frac{1}{2}\frac{N^{2}i_{\rm{a}}}{R_{\rm{q}}}\cos(2\theta)\notag\\
&\notag\\
&= -\frac{N^{2}i_{\rm{a}}}{4}\left(\frac{1}{R_{\rm{d}}}+\frac{1}{R_{\rm{q}}}\right) -\frac{1}{2}\cos(2\theta)\frac{N^{2}i_{\rm{a}}}{2}\left(\frac{1}{R_{\rm{d}}}-\frac{1}{R_{\rm{q}}}\right)\notag\\
&\qquad \qquad \qquad \qquad-\frac{\sqrt{3}}{2}\sin(2\theta)\frac{N^{2}i_{\rm{a}}}{2}\left(\frac{1}{R_{\rm{d}}}-\frac{1}{R_{\rm{q}}}\right)\notag\\
&\notag\\
&=-\frac{N^{2}i_{\rm{a}}}{4}\left(\frac{1}{R_{\rm{d}}}+\frac{1}{R_{\rm{q}}}\right) \notag\\
&\qquad \qquad \qquad + \left( -\frac{1}{2}\cos(2\theta)-\frac{\sqrt{3}}{2}\sin(2\theta)\right) \frac{N^{2}i_{\rm{a}}}{2}\left(\frac{1}{R_{\rm{d}}}-\frac{1}{R_{\rm{q}}}\right)\notag\\
\end{align}
$$
となる。
ここで、$${\cos \left(2\theta + \frac{2}{3}\pi \right)}$$を計算すると、
$$
\begin{align}
\cos\left(2\theta + \frac{2}{3}\pi \right) &= \cos(2\theta)\cos\left(\frac{2}{3}\pi \right)-\sin(2\theta)\sin\left(\frac{2}{3}\pi \right) \notag\\
&= -\frac{1}{2}\cos(2\theta)-\frac{\sqrt{3}}{2}\sin(2\theta)\notag\\
\end{align}
$$
なので、これを用いると、
$$
\begin{align}
&\notag\\
\phi_{\rm{c}} &= -\frac{N^{2}i_{\rm{a}}}{4}\left(\frac{1}{R_{\rm{d}}}+\frac{1}{R_{\rm{q}}}\right) +\cos\left(2\theta + \frac{2}{3}\pi \right)\frac{N^{2}i_{\rm{a}}}{2}\left(\frac{1}{R_{\rm{d}}}-\frac{1}{R_{\rm{q}}}\right)\notag\\
&\notag\\
&= -\frac{N^{2}i_{\rm{a}}}{4}\left(\frac{1}{R_{\rm{d}}}+\frac{1}{R_{\rm{q}}}\right) +\frac{N^{2}i_{\rm{a}}}{2}\left(\frac{1}{R_{\rm{d}}}-\frac{1}{R_{\rm{q}}}\right)\cos\left(2\theta + \frac{2}{3}\pi \right)\notag\\
\end{align}
$$
となる。
よって、$${\rm{a}}$$相と$${\rm{c}}$$相の相互インダクタンス$${L_{\rm{ac}}}$$ は、
$$
\begin{align}
L_{\rm{ac}} &= \frac{\phi_{\rm{c}}}{i_{\rm{a}}}\notag\\
&\notag\\
&=-\frac{N^{2}}{4}\left(\frac{1}{R_{\rm{d}}}+\frac{1}{R_{\rm{q}}}\right) +\frac{N^{2}}{2}\left(\frac{1}{R_{\rm{d}}}-\frac{1}{R_{\rm{q}}}\right)\cos\left(2\theta + \frac{2}{3}\pi \right) \notag\\
\end{align}
$$
となる。
$${L_{2}}$$、$${L_{3}}$$を用いて表すと、
$$
\begin{align}
L_{\rm{ac}} &=-L_{3} +L_{2}\cos\left(2\theta + \frac{2}{3}\pi \right) \notag\\
\end{align}
$$
となる。
また、相互インダクタンスは、どちらも等しいので、
$$
L_{\rm{ca}} = L_{\rm{ac}}
$$
となる。
b相の自己インダクタンス
$${\rm{a}}$$相の角度を$${-\frac{2}{3}\pi}$$ずらすと、$${\rm{b}}$$相になるので、$${\rm{b}}$$相の起磁力を回転子軸方向($${\rm{d}}$$軸)とこれに直角な方向($${\rm{q}}$$軸)の成分に分解すると、
$$
\begin{align}
F_{\rm{d}} &= Ni_{\rm{b}}\cos \left(\theta - \frac{2}{3}\pi \right)\notag\\
F_{\rm{q}} &= Ni_{\rm{b}}\sin \left(\theta - \frac{2}{3}\pi \right)\notag\\
\end{align}
$$
となる。
したがって、$${\rm{d}}$$軸および$${\rm{q}}$$軸の磁束は、
$$
\begin{align}
\phi_{\rm{d}} &= \frac{F_{\rm{d}}}{R_{\rm{d}}}\notag\\
&= \frac{Ni_{\rm{b}}}{R_{\rm{d}}}\cos \left(\theta - \frac{2}{3}\pi \right)\tag{15}\\
&\notag\\
\phi_{\rm{q}} &= \frac{F_{\rm{q}}}{R_{\rm{q}}}\notag\\
&= \frac{Ni_{\rm{b}}}{R_{\rm{q}}}\sin \left(\theta - \frac{2}{3}\pi \right)\tag{16}\\
\end{align}
$$
となる。
式(5)の関係を$${-\frac{2}{3}\pi}$$ずらせば$${\rm{b}}$$相巻線を貫く磁束になるので、$${\rm{b}}$$相巻線を貫く磁束は、
$$
\begin{align}
\phi_{\rm{b}} &= N\left(\phi_{\rm{d}} \cos\left(\theta - \frac{2}{3}\pi \right)+\phi_{\rm{q}} \sin\left(\theta - \frac{2}{3}\pi \right)\right)\notag\\
\end{align}
$$
と求まる。
式(15)と式(16)を代入すると、
$$
\begin{align}
\phi_{\rm{b}} &= \frac{N^{2}i_{\rm{b}}}{R_{\rm{d}}}\cos \left(\theta - \frac{2}{3}\pi \right) \cos \left(\theta - \frac{2}{3}\pi \right) \notag\\
&\qquad \qquad\qquad+\frac{N^{2}i_{\rm{b}}}{R_{\rm{q}}}\sin \left(\theta - \frac{2}{3}\pi \right)\sin \left(\theta - \frac{2}{3}\pi \right)\notag\\
&\notag\\
&= \frac{N^{2}i_{\rm{b}}}{R_{\rm{d}}}\left(\cos \left(\theta - \frac{2}{3}\pi \right)\right)^{2} +\frac{N^{2}i_{\rm{b}}}{R_{\rm{q}}}\left(\sin \left(\theta - \frac{2}{3}\pi \right)\right)^{2}\notag\\
\end{align}
$$
となる。
ここで、式(11)と式(12)の関係を使うと、
$$
\begin{align}
&\notag\\
\phi_{\rm{b}} &= \frac{N^{2}i_{\rm{b}}}{R_{\rm{d}}}\left(\cos \left(\theta - \frac{2}{3}\pi \right)\right)^{2} +\frac{N^{2}i_{\rm{b}}}{R_{\rm{q}}}\left(\sin \left(\theta- \frac{2}{3}\pi \right)\right)^{2}\notag\\
&\notag\\
&= \frac{N^{2}i_{\rm{b}}}{R_{\rm{d}}}\frac{1}{2}\left(1+\cos \left(2\left(\theta - \frac{2}{3}\pi \right)\right)\right ) \notag\\
&\qquad \qquad\qquad+\frac{N^{2}i_{\rm{b}}}{R_{\rm{q}}}\frac{1}{2}\left(1-\cos \left(2\left(\theta - \frac{2}{3}\pi \right)\right)\right)\notag\\
&\notag\\
&= \frac{N^{2}i_{\rm{b}}}{2R_{\rm{d}}}+\frac{N^{2}i_{\rm{b}}}{2R_{\rm{d}}}\cos \left(2\theta - \frac{4}{3}\pi \right) \notag\\
&\qquad \qquad\qquad+\frac{N^{2}i_{\rm{b}}}{2R_{\rm{q}}}-\frac{N^{2}i_{\rm{b}}}{2R_{\rm{q}}}\cos \left(2\theta - \frac{4}{3}\pi \right)\notag\\
&\notag\\
&= \frac{N^{2}i_{\rm{b}}}{2}\left(\frac{1}{R_{\rm{d}}}+\frac{1}{R_{\rm{q}}}\right)+\frac{N^{2}i_{\rm{b}}}{2}\left(\frac{1}{R_{\rm{d}}}-\frac{1}{R_{\rm{q}}}\right)\cos \left(2\theta - \frac{4}{3}\pi \right) \notag\\
\end{align}
$$
となる。
ここで、$${\cos(\theta + 2n\pi) = \cos(\theta)}$$($${n}$$は整数)の関係を用いて、$${2\pi}$$を足すと、
$$
\begin{align}
\cos \left(2\theta - \frac{4}{3}\pi +2\pi\right) &= \cos \left(2\theta + \frac{2}{3}\pi \right) \notag\\
\end{align}
$$
となるので、これを用いれば、
$$
\begin{align}
&\notag\\
\phi_{\rm{b}} &= \frac{N^{2}i_{\rm{b}}}{2}\left(\frac{1}{R_{\rm{d}}}+\frac{1}{R_{\rm{q}}}\right)+\frac{N^{2}i_{\rm{b}}}{2}\left(\frac{1}{R_{\rm{d}}}-\frac{1}{R_{\rm{q}}}\right)\cos \left(2\theta + \frac{2}{3}\pi \right) \notag\\
\end{align}
$$
となる。
よって、$${\rm{b}}$$相巻線の自己インダクタンス$${L_{\rm{bb}}}$$は、
$$
\begin{align}
L_{\rm{bb}} &= \frac{\phi_{\rm{b}}}{i_{\rm{b}}}\notag\\
&\notag\\
&= \frac{N^{2}}{2}\left(\frac{1}{R_{\rm{d}}}+\frac{1}{R_{\rm{q}}}\right)+\frac{N^{2}}{2}\left(\frac{1}{R_{\rm{d}}}-\frac{1}{R_{\rm{q}}}\right)\cos \left(2\theta + \frac{2}{3}\pi \right) \notag\\
\end{align}
$$
と求まる。
$${L_{1}}$$、$${L_{2}}$$を用いると、
$$
\begin{align}
L_{\rm{bb}} &= L_{1}+L_{2}\cos \left(2\theta + \frac{2}{3}\pi \right) \notag\\
\end{align}
$$
と表せる。
b相とc相の相互インダクタンス
$${\rm{a}}$$相の角度を$${-\frac{2}{3}\pi}$$ずらすと、$${\rm{b}}$$相になるので、$${\rm{b}}$$相と$${\rm{c}}$$相の相互インダクタンスは、$${\rm{a}}$$相と$${\rm{b}}$$相の相互インダクタンスを$${-\frac{2}{3}\pi}$$ずらせばよい。
式(9)の第1項の$${\cos}$$の中身を書き換えると、
$$
\begin{align}
\cos \left(\frac{2}{3}\pi -\theta \right) &= \cos \left(\theta - \frac{2}{3}\pi \right)=\left(\theta - \frac{2}{3}\pi - \frac{2}{3}\pi \right) &= \cos \left(\theta - \frac{4}{3}\pi \right)\notag\\
\end{align}
$$
となる。
第2項は、
$$
\begin{align}
\cos \left(\theta - \frac{\pi}{6}- \frac{2}{3}\pi\right) &= \cos \left(\theta - \frac{5}{6}\pi \right)\notag\\
\end{align}
$$
となるので、$${\rm{b}}$$相巻線を流れる電流$${i_{\rm{b}}}$$相によって、$${\rm{c}}$$相を貫く磁束は、
$$
\begin{align}
\phi_{\rm{c}} &= N\left(\phi_{\rm{d}}\cos \left(\theta -\frac{4}{3}\pi \right)-\phi_{\rm{q}}\cos \left(\theta - \frac{5}{6}\pi\right)\right)\notag\\
\end{align}
$$
となる。
式(15)と式(16)を代入すると、
$$
\begin{align}
&\notag\\
\phi_{\rm{c}} &= \frac{N^{2}i_{\rm{b}}}{R_{\rm{d}}}\cos \left(\theta - \frac{2}{3}\pi \right)\cos \left(\theta-\frac{4}{3}\pi \right)\notag\\
&\qquad \qquad \qquad- \frac{N^{2}i_{\rm{b}}}{R_{\rm{q}}}\sin \left(\theta - \frac{2}{3}\pi \right)\cos \left(\theta - \frac{5}{6}\pi\right)\notag\\
&\notag\\
\end{align}
$$
となる。
ここで、$${\cos \left(\theta-\frac{2}{3}\pi \right)}$$、$${\sin \left(\theta - \frac{2}{3}\pi \right)}$$、$${\cos \left(\theta-\frac{4}{3}\pi \right)}$$および$${\cos \left(\theta - \frac{5}{6}\pi\right)}$$を加法定理を用いて書き換えると、
$$
\begin{align}
\cos \left(\theta-\frac{2}{3}\pi \right)&= \cos(\theta)\cos\left(\frac{2}{3}\pi \right) + \sin(\theta)\sin\left(\frac{2}{3}\pi \right) \notag\\
&= -\frac{1}{2} \cos(\theta) + \frac{\sqrt{3}}{2} \sin(\theta) \notag\\
\end{align}
$$
$$
\begin{align}
\sin \left(\theta - \frac{2}{3}\pi \right)&= \sin(\theta)\cos\left( \frac{2}{3}\pi \right) -\cos(\theta) \sin\left( \frac{2}{3}\pi\right) \notag\\
&= -\frac{1}{2} \sin(\theta) - \frac{\sqrt{3}}{2} \cos(\theta) \notag\\
\end{align}
$$
$$
\begin{align}
\cos \left(\theta-\frac{4}{3}\pi \right)&=\cos(\theta) \cos\left(\frac{4}{3}\pi \right) + \sin(\theta)\sin\left(\frac{4}{3}\pi \right) \notag\\
&= -\frac{1}{2} \cos(\theta) - \frac{\sqrt{3}}{2} \sin(\theta) \notag\\
\end{align}
$$
$$
\begin{align}
\cos \left(\theta - \frac{5}{6}\pi\right)&= \cos(\theta)\cos\left( \frac{5}{6}\pi \right) +\sin(\theta) \sin\left(\frac{5}{6}\pi \right) \notag\\
&= -\frac{\sqrt{3}}{2} \cos(\theta) + \frac{1}{2} \sin(\theta) \notag\\
\end{align}
$$
となる。これを代入すると、
$$
\begin{align}
\phi_{\rm{c}} &= \frac{N^{2}i_{\rm{b}}}{R_{\rm{d}}}\left(-\frac{1}{2} \cos(\theta) + \frac{\sqrt{3}}{2} \sin(\theta) \right)\left( -\frac{1}{2} \cos(\theta) - \frac{\sqrt{3}}{2} \sin(\theta) \right)\notag\\
&\qquad - \frac{N^{2}i_{\rm{b}}}{R_{\rm{q}}}\left(-\frac{1}{2} \sin(\theta) - \frac{\sqrt{3}}{2} \cos(\theta) \right) \left( -\frac{\sqrt{3}}{2} \cos(\theta) + \frac{1}{2} \sin(\theta)\right)\notag\\
&\notag\\
&= \frac{N^{2}i_{\rm{b}}}{R_{\rm{d}}}\biggl (\frac{1}{4} \left(\cos(\theta)\right)^{2} + \frac{\sqrt{3}}{4} \cos(\theta)\sin(\theta)\notag\\
&\qquad \qquad \qquad \qquad \qquad- \frac{\sqrt{3}}{4} \cos(\theta)\sin(\theta) -\frac{3}{4} \left(\sin(\theta)\right)^{2} \biggr) \notag\\
&\qquad - \frac{N^{2}i_{\rm{b}}}{R_{\rm{q}}}\biggl (\frac{\sqrt{3}}{4} \cos(\theta)\sin(\theta) -\frac{1}{4} \left(\sin(\theta)\right)^{2}\notag\\
&\qquad \qquad \qquad \qquad \qquad+\frac{3}{4} \left(\cos(\theta)\right)^{2} - \frac{\sqrt{3}}{4} \cos(\theta)\sin(\theta)\biggr) \notag\\
&\notag\\
&= \frac{N^{2}i_{\rm{b}}}{R_{\rm{d}}}\left (\frac{1}{4} \left(\cos(\theta)\right)^{2} -\frac{3}{4} \left(\sin(\theta)\right)^{2} \right) \notag\\
&\qquad \qquad \qquad \qquad - \frac{N^{2}i_{\rm{b}}}{R_{\rm{q}}}\left (\frac{3}{4} \left(\cos(\theta)\right)^{2}-\frac{1}{4} \left(\sin(\theta)\right)^{2} \right)\notag\\
\end{align}
$$
となる。
ここで$${ \left(\cos(\theta)\right)^{2}+ \left(\sin(\theta)\right)^{2}=1}$$を用いると、
$$
\begin{align}
&\notag\\
\phi_{\rm{c}} &= \frac{N^{2}i_{\rm{b}}}{R_{\rm{d}}}\left (\frac{1}{4} \left(\cos(\theta)\right)^{2} -\frac{3}{4} \left(\sin(\theta)\right)^{2} \right) \notag\\
&\qquad \qquad \qquad \qquad - \frac{N^{2}i_{\rm{b}}}{R_{\rm{q}}}\left (\frac{3}{4} \left(\cos(\theta)\right)^{2}-\frac{1}{4} \left(\sin(\theta)\right)^{2} \right)\notag\\
&\notag\\
&= \frac{N^{2}i_{\rm{b}}}{R_{\rm{d}}}\left (\frac{1}{4} \left(\cos(\theta)\right)^{2} -\frac{3}{4} \left(1- (\cos(\theta))^{2} \right) \right) \notag\\
&\qquad \qquad \qquad \qquad - \frac{N^{2}i_{\rm{b}}}{R_{\rm{q}}}\left (\frac{3}{4} \left(\cos(\theta)\right)^{2}-\frac{1}{4} \left(1- (\cos(\theta))^{2} \right) \right)\notag\\
&\notag\\
&= \frac{N^{2}i_{\rm{b}}}{R_{\rm{d}}}\left (\frac{1}{4} \left(\cos(\theta)\right)^{2} -\frac{3}{4}+\frac{3}{4} (\cos(\theta))^{2} \right) \notag\\
&\qquad \qquad \qquad \qquad - \frac{N^{2}i_{\rm{b}}}{R_{\rm{q}}}\left (\frac{3}{4} \left(\cos(\theta)\right)^{2}-\frac{1}{4} +\frac{1}{4} (\cos(\theta))^{2} \right)\notag\\
&\notag\\
&= \frac{N^{2}i_{\rm{b}}}{R_{\rm{d}}}\left ( \left(\cos(\theta)\right)^{2} -\frac{3}{4} \right)- \frac{N^{2}i_{\rm{b}}}{R_{\rm{q}}}\left (\left(\cos(\theta)\right)^{2}-\frac{1}{4} \right)\notag\\
&\notag\\
&= \frac{N^{2}i_{\rm{b}}}{R_{\rm{d}}}\left(\cos(\theta)\right)^{2} -\frac{3}{4} \frac{N^{2}i_{\rm{b}}}{R_{\rm{d}}} - \frac{N^{2}i_{\rm{b}}}{R_{\rm{q}}}\left(\cos(\theta)\right)^{2}+\frac{1}{4}\frac{N^{2}i_{\rm{b}}}{R_{\rm{q}}}\notag\\
\end{align}
$$
ここで式(11)を用いると、
$$
\begin{align}
\phi_{\rm{c}} &= \frac{N^{2}i_{\rm{b}}}{R_{\rm{d}}}\left(\cos(\theta)\right)^{2} -\frac{3}{4} \frac{N^{2}i_{\rm{b}}}{R_{\rm{q}}} - \frac{N^{2}i_{\rm{b}}}{R_{\rm{q}}}\left(\cos(\theta)\right)^{2}+\frac{1}{4}\frac{N^{2}i_{\rm{b}}}{R_{\rm{q}}}\notag\\
&\notag\\
&= \frac{N^{2}i_{\rm{b}}}{R_{\rm{d}}}\frac{1}{2}\left(\cos(2\theta)+1\right) -\frac{3}{4} \frac{N^{2}i_{\rm{b}}}{R_{\rm{d}}} - \frac{N^{2}i_{\rm{b}}}{R_{\rm{q}}}\frac{1}{2}\left(\cos(2\theta)+1\right)+\frac{1}{4}\frac{N^{2}i_{\rm{b}}}{R_{\rm{q}}}\notag\\
&\notag\\
&= \frac{N^{2}i_{\rm{b}}}{2R_{\rm{d}}}\cos(2\theta)+\frac{N^{2}i_{\rm{b}}}{2R_{\rm{d}}} -\frac{3}{4} \frac{N^{2}i_{\rm{b}}}{R_{\rm{d}}} - \frac{N^{2}i_{\rm{b}}}{2R_{\rm{q}}}\cos(2\theta)-\frac{N^{2}i_{\rm{b}}}{2R_{\rm{q}}}+\frac{1}{4}\frac{N^{2}i_{\rm{b}}}{R_{\rm{q}}}\notag\\
&\notag\\
&= \frac{N^{2}i_{\rm{b}}}{2R_{\rm{d}}}\cos(2\theta)- \frac{N^{2}i_{\rm{b}}}{2R_{\rm{q}}}\cos(2\theta) -\frac{1}{4} \frac{N^{2}i_{\rm{b}}}{R_{\rm{d}}} -\frac{1}{4}\frac{N^{2}i_{\rm{b}}}{R_{\rm{q}}}\notag\\
&\notag\\
&= \frac{N^{2}i_{\rm{b}}}{2}\left(\frac{1}{R_{\rm{d}}}-\frac{1}{R_{\rm{q}}}\right)\cos(2\theta)-\frac{N^{2}i_{\rm{b}}}{4} \left(\frac{1}{R_{\rm{d}}}+\frac{1}{R_{\rm{q}}}\right)\notag\\
\end{align}
$$
と求まる。
よって、$${\rm{b}}$$相と$${\rm{c}}$$相の相互インダクタンス$${L_{\rm{bc}}}$$ は、
$$
\begin{align}
L_{\rm{bc}} &= \frac{\phi_{\rm{c}}}{i_{\rm{b}}}\notag\\
&\notag\\
&=\frac{N^{2}}{2}\left(\frac{1}{R_{\rm{d}}}-\frac{1}{R_{\rm{q}}}\right)\cos(2\theta)-\frac{N^{2}}{4} \left(\frac{1}{R_{\rm{d}}}+\frac{1}{R_{\rm{q}}}\right)\notag\\
\end{align}
$$
となる。
$${L_{2}}$$、$${L_{3}}$$を用いて表すと、
$$
\begin{align}
L_{\rm{bc}} &=-L_{3} +L_{2}\cos\left(2\theta \right) \notag\\
\end{align}
$$
となる。
また、相互インダクタンスは、どちらも等しいので、
$$
L_{\rm{bc}} = L_{\rm{cb}}
$$
となる。
c相の自己インダクタンス
$${\rm{a}}$$相の角度を$${-\frac{4}{3}\pi}$$または、$${\frac{2}{3}\pi}$$ずらすと、$${\rm{c}}$$相になるので、$${\rm{c}}$$相の起磁力を回転子軸方向($${d}$$軸)とこれに直角な方向($${q}$$軸)の成分に分解すると、
$$
\begin{align}
F_{\rm{d}} &= Ni_{\rm{c}}\cos \left(\theta - \frac{4}{3}\pi \right)\notag\\
F_{\rm{q}} &= Ni_{\rm{c}}\sin \left(\theta - \frac{4}{3}\pi \right)\notag\\
\end{align}
$$
となる。
したがって、$${d}$$軸および$${q}$$軸の磁束は、
$$
\begin{align}
\phi_{\rm{d}} &= \frac{F_{\rm{d}}}{R_{\rm{d}}}\notag\\
&= \frac{Ni_{\rm{c}}}{R_{\rm{d}}}\cos \left(\theta - \frac{4}{3}\pi \right)\tag{17}\\
&\notag\\
\phi_{\rm{q}} &= \frac{F_{\rm{q}}}{R_{\rm{q}}}\notag\\
&= \frac{Ni_{\rm{c}}}{R_{\rm{q}}}\sin \left(\theta - \frac{4}{3}\pi \right)\tag{18}\\
\end{align}
$$
となる。
式(5)の関係を$${-\frac{4}{3}\pi}$$ずらせば$${\rm{c}}$$相巻線を貫く磁束になるので、$${\rm{c}}$$相巻線を貫く磁束は、
$$
\begin{align}
\phi_{\rm{c}} &= N\left(\phi_{\rm{d}} \cos\left(\theta - \frac{4}{3}\pi \right)+\phi_{\rm{q}} \sin\left(\theta - \frac{4}{3}\pi \right)\right)\notag\\
\end{align}
$$
と求まる。
式(17)と式(18)を代入すると、
$$
\begin{align}
&\notag\\
\phi_{\rm{c}} &= \frac{N^{2}i_{\rm{c}}}{R_{\rm{d}}}\cos \left(\theta - \frac{4}{3}\pi \right) \cos \left(\theta - \frac{4}{3}\pi \right) \notag\\
&\qquad \qquad\qquad+\frac{N^{2}i_{\rm{c}}}{R_{\rm{q}}}\sin \left(\theta - \frac{4}{3}\pi \right)\sin \left(\theta - \frac{4}{3}\pi \right)\notag\\
&\notag\\
&= \frac{N^{2}i_{\rm{c}}}{R_{\rm{d}}}\left(\cos \left(\theta - \frac{4}{3}\pi \right)\right)^{2} +\frac{N^{2}i_{\rm{c}}}{R_{\rm{q}}}\left(\sin \left(\theta - \frac{4}{3}\pi \right)\right)^{2}\notag\\
\end{align}
$$
となる。
ここで、式(11)と式(12)の関係を使うと、
$$
\begin{align}
&\notag\\
\phi_{\rm{c}} &= \frac{N^{2}i_{\rm{c}}}{R_{\rm{d}}}\left(\cos \left(\theta - \frac{4}{3}\pi \right)\right)^{2} +\frac{N^{2}i_{\rm{c}}}{R_{\rm{q}}}\left(\sin \left(\theta- \frac{4}{3}\pi \right)\right)^{2}\notag\\
&\notag\\
&= \frac{N^{2}i_{\rm{c}}}{R_{\rm{d}}}\frac{1}{2}\left(1+\cos \left(2\left(\theta - \frac{4}{3}\pi \right)\right)\right ) \notag\\
&\qquad \qquad\qquad+\frac{N^{2}i_{\rm{c}}}{R_{\rm{q}}}\frac{1}{2}\left(1-\cos \left(2\left(\theta - \frac{4}{3}\pi \right)\right)\right)\notag\\
&\notag\\
&= \frac{N^{2}i_{\rm{c}}}{2R_{\rm{d}}}+\frac{N^{2}i_{\rm{c}}}{2R_{\rm{d}}}\cos \left(2\theta - \frac{8}{3}\pi \right) \notag\\
&\qquad \qquad\qquad+\frac{N^{2}i_{\rm{c}}}{2R_{\rm{q}}}-\frac{N^{2}i_{\rm{c}}}{2R_{\rm{q}}}\cos \left(2\theta - \frac{8}{3}\pi \right)\notag\\
&\notag\\
&= \frac{N^{2}i_{\rm{c}}}{2}\left(\frac{1}{R_{\rm{d}}}+\frac{1}{R_{\rm{q}}}\right)+\frac{N^{2}i_{\rm{c}}}{2}\left(\frac{1}{R_{\rm{d}}}-\frac{1}{R_{\rm{q}}}\right)\cos \left(2\theta - \frac{8}{3}\pi \right) \notag\\
\end{align}
$$
となる。
ここで、$${\cos(\theta + 2n\pi) = \cos(\theta)}$$($${n}$$は整数)の関係を用いて、$${2\pi}$$を足すと、
$$
\begin{align}
\cos \left(2\theta - \frac{8}{3}\pi +2\pi\right) &= \cos \left(2\theta - \frac{2}{3}\pi \right) \notag\\
\end{align}
$$
となるので、これを用いれば、
$$
\begin{align}
&\notag\\
\phi_{\rm{c}} &= \frac{N^{2}i_{\rm{c}}}{2}\left(\frac{1}{R_{\rm{d}}}+\frac{1}{R_{\rm{q}}}\right)+\frac{N^{2}i_{\rm{c}}}{2}\left(\frac{1}{R_{\rm{d}}}-\frac{1}{R_{\rm{q}}}\right)\cos \left(2\theta - \frac{2}{3}\pi \right) \notag\\
\end{align}
$$
となる。
よって、$${\rm{c}}$$相巻線の自己インダクタンス$${L_{\rm{cc}}}$$は、
$$
\begin{align}
L_{\rm{cc}} &= \frac{\phi_{\rm{c}}}{i_{\rm{c}}}\notag\\
&\notag\\
&= \frac{N^{2}}{2}\left(\frac{1}{R_{\rm{d}}}+\frac{1}{R_{\rm{q}}}\right)+\frac{N^{2}}{2}\left(\frac{1}{R_{\rm{d}}}-\frac{1}{R_{\rm{q}}}\right)\cos \left(2\theta - \frac{2}{3}\pi \right) \notag\\
\end{align}
$$
と求まる。
$${L_{1}}$$、$${L_{2}}$$を用いると、
$$
\begin{align}
L_{\rm{cc}} &= L_{1}+L_{2}\cos \left(2\theta - \frac{2}{3}\pi \right) \notag\\
\end{align}
$$
と表せる。
励磁巻線の自己インダクタンスと相互インダクタンス
励磁巻線の自己インダクタンスは、図10に示すように磁路の性質は、回転子の位置によらず一定である。

そのため、回転子の位置$${\theta}$$によらないので、
$$
L_{\rm{ff}} = 一定
$$
となる。
電機子巻線と励磁巻線の相互インダクタンスは、図11に示すように$${\rm{a}}$$相巻線と回転子軸が一致した時に最大値となる。また、$${\rm{a}}$$相巻線と回転子軸が直交した時に$${0}$$、$${\rm{a}}$$相巻線と回転子軸が反対方向になった時に最小値を取る。

よって、相互インダクタンスの最大値を$${L_{\rm{afm}}}$$とすれば、
$$
L_{\rm{af}} = L_{\rm{afm}}\cos(\theta)
$$
と表せる。
$${\rm{b}}$$相巻線と励磁巻線の相互インダクタンスおよび$${\rm{c}}$$相巻線と励磁巻線の相互インダクタンスは、
$$
\begin{align}
&\notag\\
L_{\rm{bf}} &= L_{\rm{afm}}\cos\left(\theta-\frac{2}{3}\pi\right)\notag\\
&\notag\\
L_{\rm{cf}} &= L_{\rm{afm}}\cos\left(\theta+\frac{2}{3}\pi\right)\notag\\
\end{align}
$$
となる。
インダクタンスのまとめ
自己インダクタンス
$$
\begin{align}
L_{\rm{aa}} &= L_{1}+L_{2}\cos \left(2\theta \right)\notag\\
L_{\rm{bb}} &= L_{1}+L_{2}\cos \left(2\theta + \frac{2}{3}\pi \right)\notag\\
L_{\rm{cc}} &= L_{1}+L_{2}\cos \left(2\theta - \frac{2}{3}\pi \right)\notag\\
L_{\rm{ff}} &= 一定\notag\\
\end{align}
$$
相互インダクタンス
$$
\begin{align}
L_{\rm{ab}}&= L_{\rm{ba}}= -L_{3} +L_{2}\cos\left(2\theta - \frac{2}{3}\pi \right)\notag\\
L_{\rm{bc}}&= L_{\rm{cb}}= -L_{3}+L_{2}\cos \left(2\theta \right)\notag\\
L_{\rm{ca}}&= L_{\rm{ac}}= -L_{3} +L_{2}\cos\left(2\theta + \frac{2}{3}\pi \right)\notag\\
L_{\rm{af}} &= L_{\rm{afm}}\cos(\theta)\notag\\
L_{\rm{bf}} &= L_{\rm{afm}}\cos(\theta-\frac{2}{3}\pi)\notag\\
L_{\rm{cf}} &= L_{\rm{afm}}\cos(\theta+\frac{2}{3}\pi)\notag\\
\end{align}
$$
関連記事
加法定理と加法定理から導かれる式
https://note.com/elemag/n/na27cb4b719c8?sub_rt=share_pw
サイト
https://sites.google.com/view/elemagscience/%E3%83%9B%E3%83%BC%E3%83%A0
この記事が気に入ったらサポートをしてみませんか?
