
令和4年度下期 機械科目 問15 電験3種過去問
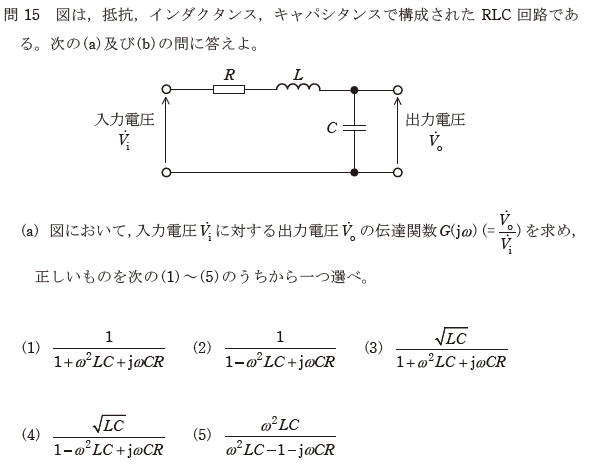
問題
考え方
(a)は、周波数伝達関数を求める問題である。問題文は伝達関数$${G(j\omega)}$$を求めよとなっているが、$${(j\omega)}$$は、周波数伝達関数を表す。
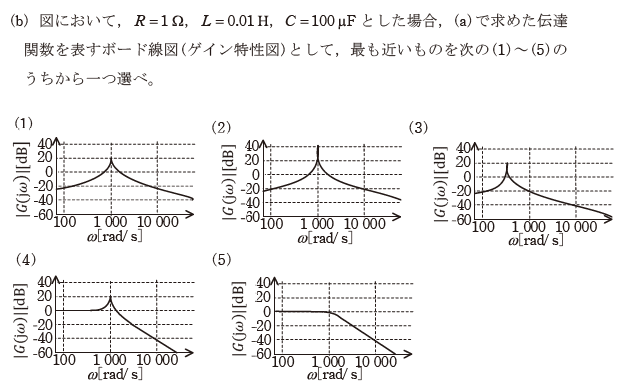
(b)はボード線図を問う問題であるが、$${\omega}$$の値を変化させたときの場合分けをしながら考える。
解答例
(a)
回路に流れる電流$${i(t)}$$を考慮し、電圧方程式を立てて、ラプラス変換するのが、もっともなやり方である。しかし、周波数伝達関数の場合は、交流回路の計算をしていることと等価になる。そのため、回路の電流を$${\dot{I}}$$として、
$$
\begin{align}
\dot{V}_{i} &= \left(R+j\omega L+ \frac{1}{j\omega C}\right)\dot{I} \tag{1}\\
\dot{V}_{o} &=\frac{1}{j\omega C} \dot{I}\tag{2}\\
\end{align}
$$
よって、周波数伝達関数$${G(j\omega)}$$は、
$$
\begin{align}
G(j\omega) &= \frac{\dot{V}_{o}}{\dot{V}_{i} } \notag\\
&= \frac{\frac{1}{j\omega C}\dot{I}}{\left(R+j\omega L+ \frac{1}{j\omega C}\right)\dot{I}} \notag\\
&= \frac{\frac{1}{j\omega C}}{R+j\omega L+ \frac{1}{j\omega C}} \notag\\
&= \frac{\frac{1}{j\omega C}}{R+j\omega L+ \frac{1}{j\omega C}} \times \frac{j\omega C}{j\omega C}\notag\\
&= \frac{1}{j\omega CR-\omega^{2}LC+1}\notag\\
&= \frac{1}{1-\omega^{2}LC+j\omega CR}\tag{3}
\end{align}
$$
と求まる。よって(a)の答えは、(2)である。
(b)
式(3)の対数ゲインを求めると、
$$
\begin{align}
20\log_{10}(|G(j\omega)|) &= 20\log_{10}\left(\frac{1}{\sqrt{\left(1-\omega^{2}LC\right)^{2}+\left(\omega CR\right)^{2}}}\right) \,{\rm[dB]}\tag{4}\\
\end{align}
$$
となり、式(4)に問題分の数値を代入して計算すると、
$$
\begin{align}
20\log_{10}(|G(j\omega)|) &= 20\log_{10}\left(\frac{1}{\sqrt{\left(1-10^{-6}\omega^{2}\right)^{2}+\left(10^{-4}\omega \right)^{2}}}\right)\,{\rm[dB]} \tag{5}\\
\end{align}
$$
になる。
式(5)で$${\omega}$$が変化したときを考える。
問題のグラフを参考に$${\omega = 100}$$、$${\omega = 1000}$$、$${\omega = 10000}$$の時を考える。
$${\omega = 100}$$の時
$$
\begin{align}
20\log_{10}(|G(j\omega)|) &= 20\log_{10}\left(\frac{1}{\sqrt{\left(1-10^{-6}\times 100^{2}\right)^{2}+\left(10^{-4}\times 100 \right)^{2}}}\right) \notag\\
&= 20\log_{10}\left(\frac{1}{\sqrt{\left(1-0.01\right)^{2}+\left(0.01 \right)^{2}}}\right)\,{\rm[dB]} \tag{6}\\
\end{align}
$$
式(6)において、$${\log}$$の値をまともに計算する必要はない。$${\log}$$の中身に注目してみると、$${\sqrt{\left(1-0.01\right)^{2}+\left(0.01 \right)^{2}}}$$の値は、ほぼ$${1}$$である。よって、$${\log_{10}(1)}$$を考えればよく。$${\log_{10}(1)=0}$$なので、$${\omega = 100}$$の時は、$${0\,[{\rm{dB}}]}$$となる。
$${\omega = 1000}$$の時
$$
\begin{align}
20\log_{10}(|G(j\omega)|) &= 20\log_{10}\left(\frac{1}{\sqrt{\left(1-10^{-6}\times 1000^{2}\right)^{2}+\left(10^{-4}\times 1000 \right)^{2}}}\right) \notag\\
&= 20\log_{10}\left(\frac{1}{\sqrt{\left(1-1\right)^{2}+\left(0.1 \right)^{2}}}\right) \notag\\
&= 20\log_{10}\left(\frac{1}{\sqrt{\left(0.1 \right)^{2}}}\right)\,{\rm[dB]} \tag{7}\\
\end{align}
$$
式(7)の$${\log}$$の中身に注目してみると、$${\frac{1}{\sqrt{\left(0.1 \right)^{2}}}}$$の値は、$${10}$$である。よって、$${\log_{10}(10)}$$を考えればよく。$${\log_{10}(10)=1}$$なので、$${\omega = 1000}$$の時は、$${20\,[{\rm{dB}}]}$$となる。
$${\omega = 10000}$$の時
$$
\begin{align}
20\log_{10}(|G(j\omega)|) &= 20\log_{10}\left(\frac{1}{\sqrt{\left(1-10^{-6}\times 10000^{2}\right)^{2}+\left(10^{-4}\times 10000 \right)^{2}}}\right) \notag\\
&= 20\log_{10}\left(\frac{1}{\sqrt{\left(1-100\right)^{2}+1}}\right)\,{\rm[dB]} \tag{8}\\
\end{align}
$$
式(8)の$${\log}$$の中身に注目してみると、$${\sqrt{\left(1-100\right)^{2}+1}}$$の値は、ほぼ$${100}$$である。よって、$${\log_{10}(10^{-2})}$$を考えればよく。
$${\log_{10}\left(10^{-2}\right)=-2\log_{10}(10)=-2}$$なので、$${\omega = 10000}$$の時は、$${-40\,[{\rm{dB}}]}$$となる。
以上をまとめると、
$${\omega = 100}$$の時、$${0\,[{\rm{dB}}]}$$
$${\omega = 1000}$$の時、$${20\,[{\rm{dB}}]}$$
$${\omega = 10000}$$の時、$${-40\,[{\rm{dB}}]}$$
となり、該当するグラフは、(4)である。
よって、(b)の答えは(4)となる。
サイト
https://sites.google.com/view/elemagscience/%E3%83%9B%E3%83%BC%E3%83%A0
この記事が気に入ったらサポートをしてみませんか?
