
三相誘導電動機の等価回路
三相誘導電動機
三相誘導電動機の構造としては、固定子に三相巻線があり、回転子は、かご形もしくは、巻線形である。
固定子が作る回転磁界に対して、回転子の回転速度は遅れて回転する。この遅れ具合を表すものとして、すべりがある。
すべり$${s}$$は、同期速度を$${N_{0}}$$、回転子の回転速度を$${N}$$とすれば、
$$
s = \frac{N_{0}-N}{N_{0}}\tag{1}
$$
と表される。
式(1)において、回転子が停止しているときと、同期速度で回転しているときのすべりを求めてみると、
停止時
$$
s = \frac{N_{0}-0}{N_{0}}=1\tag{2}
$$
同期速度で回転しているとき
$$
s=\frac{N_{0}-N_{0}}{N_{0}}=0\tag{3}
$$
となるため、すべりは、停止時が$${s=1}$$となる。
回転子が停止しているときの誘導電動機を考える。
誘導電動機の固定子巻線に電流を流すと、回転磁界が生じる。回転磁界は、磁束の時間的変化を生み出す。このときの回転磁界は、$${N_{0}}$$で回転しており、回転子に誘導起電力$${\dot{E}_{2}}$$が生じる。
回転子が回転しているときは、磁束の時間変化が、回転磁界と回転子の回転速度の相対速度$${N_{0}-N}$$になる。この相対速度は、式(1)より、$${sN_{0}}$$と表すことができ、回転子が停止しているときの回転磁界の$${s}$$倍である。
よって、回転子には誘導起電力$${s\dot{E}_{2}}$$が生じる。
ファラデーの電磁誘導の式からも考えることができる。回転子が停止しているときは、
$$
\dot{E}_{2}=-N_{2}\frac{{\rm{d}}\Phi}{{\rm{d}}t}\tag{4}
$$
において、$${\frac{{\rm{d}}\Phi}{{\rm{d}}t}}$$が、
$$
\frac{{\rm{d}}\Phi}{{\rm{d}}t} \propto N_{0}\tag{5}
$$
である。よって、誘導起電力$${\dot{E}_{2}}$$は、
$$
\dot{E}_{2}\propto N_{0}\tag{6}
$$
となり、同期速度に比例する。
回転子が回転しているときは、回転磁界との相対速度が$${N_{0}-N}$$となる。この相対速度は、式(1)より$${sN_{0}}$$なので、磁束の時間変化は、
$$
\frac{{\rm{d}}\Phi}{{\rm{d}}t} \propto sN_{0}\tag{7}
$$
となるため、誘導起電力$${\dot{E}_{2}}$$は、式(6)より$${s\dot{E}_{2}}$$となる。
同期速度$${N_{0}}$$は、周波数を$${f}$$、極数$${p}$$とすれば、
$$
N_{0} = \frac{120f}{p}\tag{8}
$$
で求まるため、周波数と同期速度は比例する。
回転子が停止しているときの回転子回路の周波数$${f_{2}}$$は、固定子の周波数と同じになるので、$${f_{2}=f_{1}}$$となる。
回転子が回転しているときの回転子回路の周波数$${f_{2}}$$は、相対速度が$${sN_{0}}$$で表せるため、固定子の周波数の$${s}$$倍となり、$${f_{2}=sf_{1}}$$となる。
固定子が作る磁束変化により、回転子に誘導起電力が生じるので、三相誘導電動機は、変圧器と同様に考えることができる。そのため、以降は固定子側を一次側、回転子側を二次側と呼ぶことにする。また、回転子はかご形と巻線形で等価回路は変わらないため、特に区別しない。
二次側の抵抗を$${r_{2}}$$、リアクタンスを$${x_{2}}$$とすると、二次側回路は、図1に示すような回路となる。

図1において、リアクタンスは、周波数に比例するため、回転子が回転しているときは、二次側の誘導起電力$${\dot{E}_{2}}$$と同様に、すべり$${s}$$に比例する。図1の回路では、二次側の誘導起電力$${\dot{E}_{2}}$$がすべりによって変化してしまうため、すべりで割ると、図2のようになる。
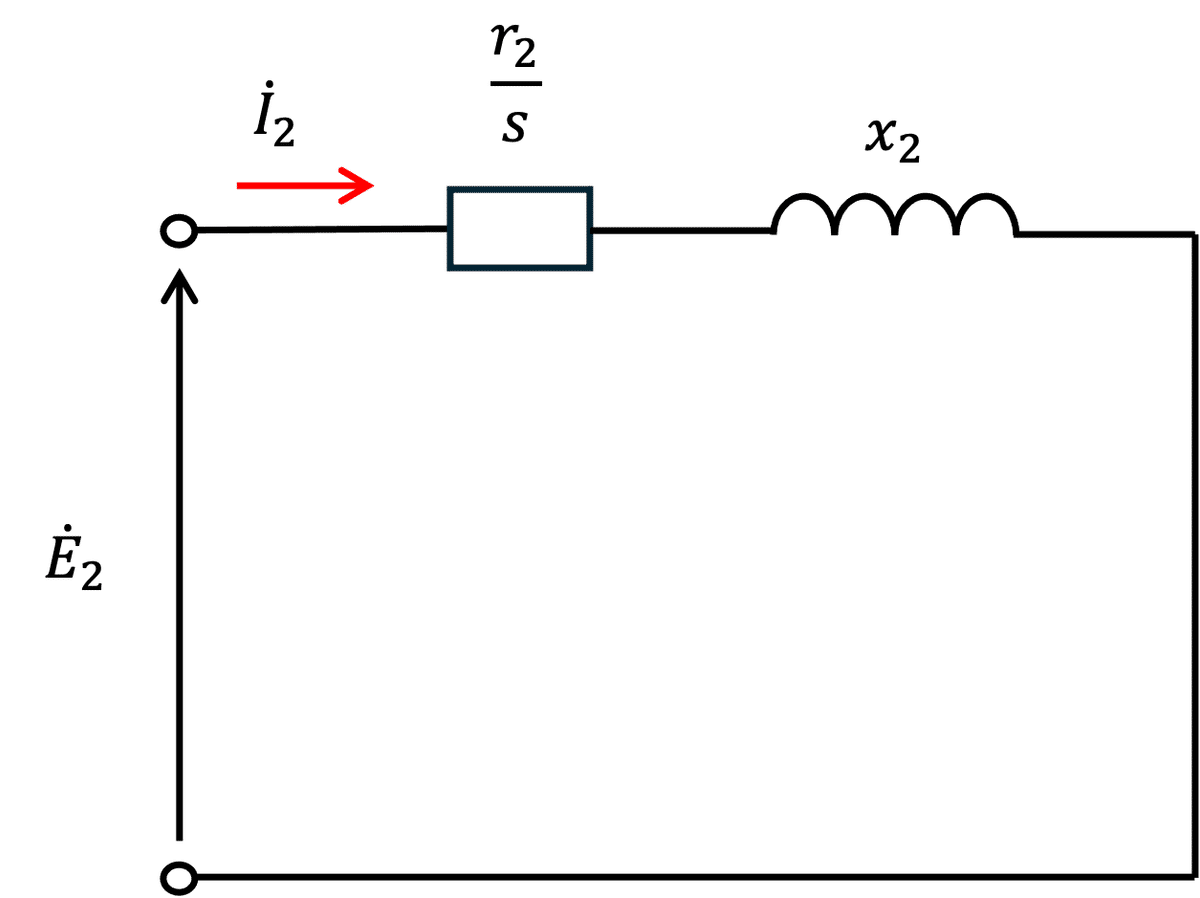
図2では、二次側の誘導起電力$${\dot{E}_{2}}$$は、すべり$${s}$$によらない値となった。一方で、二次側の抵抗部分が$${\frac{r_{2}}{s}}$$となった。二次側の巻線抵抗(かご形の場合は、導体の抵抗)を$${r_{2}}$$とすれば、
$$
\frac{r_{2}}{s}-r_{2}=\frac{1-s}{s}r_{2}\tag{9}
$$
と二次側の抵抗を分割することができる。二次側の抵抗を分割した回路は、図3のようになる。$${\frac{1-s}{s}r_{2}}$$は、三相誘導電動機の負荷抵抗と考えることができる。

一次側は、関連記事の変圧器の等価回路と同様に考えることができるため、三相誘導電動機の1相分の等価回路は、図4に示すような回路になる。

T型等価回路
関連記事の変圧器の等価回路と同様に、理想変圧器を取り除くと、図5に示す回路が得られる。これをT型等価回路という。

二次側のパラメータは一次側に換算されており、三相誘導電動機の一次側と二次側の巻数比を$${a}$$とすれば、
$$
\begin{align}
{\dot{I}_{1}}^{\prime} &= \frac{\dot{I}_{2}}{a}\tag{10}\\
{r_{2}}^{\prime} &= a^{2}r_{2}\tag{11}\\
{x_{2}}^{\prime} &= a^{2}x_{2}\tag{12}\\
\end{align}
$$
となる。
L型等価回路
T型等価回路では、励磁回路が中央にあるため、計算が複雑になる。そのため、励磁回路を電源側に移動させると、図6に示す回路となる。これをL型等価回路という。

このようなことができるのは、一次側のインピーダンス降下が一次電圧に比べて、十分に小さいこと、かつ励磁電流が一次電流に比べて十分小さいことが成立する場合である。幸いにも現実的には、L型等価回路で計算を行っても、十分な精度を保てることがほとんどである。そのため、通常はL型等価回路が使用される。
しかし、精密に三相誘導電動機を取り扱う必要がある場合は、T型等価回路を用いる必要がある。
関連記事
変圧器の等価回路
https://note.com/elemag/n/n07e1f3b1b9d3?sub_rt=share_pw
サイト
https://sites.google.com/view/elemagscience/%E3%83%9B%E3%83%BC%E3%83%A0
この記事が気に入ったらサポートをしてみませんか?
