MATLABで学ぶ振動工学 メタマテリアル・周期構造(平面構造・シェル構造)
1.はじめに
最近は「メタマテリアル」というワードを良く聞きますよね。
私自身もこの分野に非常に可能性を感じており、自己研鑽も兼ねて勉強しています。
メタマテリアルは「周期構造」や「周期構造物」とも呼ばれ、分散関係を導出するとバンドギャップを持つ構造を指します。
一般的に、振動工学や振動モード解析などの分野では、振動モード、共振周波数などのモード次元や周波数次元で考えることが多いです。この流れで、メタマテリアルや周期構造を理解しようとするとうまくいきません。メタマテリアルや周期構造を理解するためには、「波動」的な考え方が必要です。
こちらで(外部リンク)で1次元モデルを用いてメタマテリアルの基礎について説明したので、基礎的な知識を得たい方は参考にして頂けると幸いです。
このnoteでは2次元モデル(平面構造・シェル構造)についてMATLABプログラムを用いて説明します。
ちなみに、この記事の構造モデルや計算結果の検証には、下記文献を参考にしています。
2019年 機械学会(Dynamics and Design Conference)
"周期構造の弾性波バンドギャップに基づくシェル構造の振動低減"
豊田中央研究所 富田直, 西垣英一, 表竜二
https://www.jstage.jst.go.jp/article/jsmedmc/2019/0/2019_109/_article/-char/ja/
天下の豊田中研様の論文です。
しかし、この参考文献だけではプログラムを作ることはできません。論文にはよくあることですが、”論文として発表したいけど、内容は教えたくない。でも、すごいことしているように思われたい”ということが根底にあるかと思います。本参考文献もそんな感じです。
プログラムを書けるぐらい論文を紐解くには、関連する論文をざっと10冊程度読まないと厳しい、といのが実状かと思いますが、私は趣味で勉強しているので、ここでは余すことなく情報展開していきます。
2.メタマテリアルの構造・モデル
参考文献からこの記事用にモデルを作成しました。
なお、参考文献よりも節点(ノード)を大幅に削減して、自由度を低減しています。(下記リンクでモデルを提供するには容量を低減する必要があったため)
また、MK行列は自作のシェルプログラムで構築しているので、論文の結果とは一致しませんので、ご了承ください。
この記事で使用するユニットセルのモデルは下記です。このユニットセルが連続して並んでいる平板がメタマテリアルだと思ってください。ただし、メタマテリアルの性能はユニットセルで決まるので、下記モデルだけを扱います。
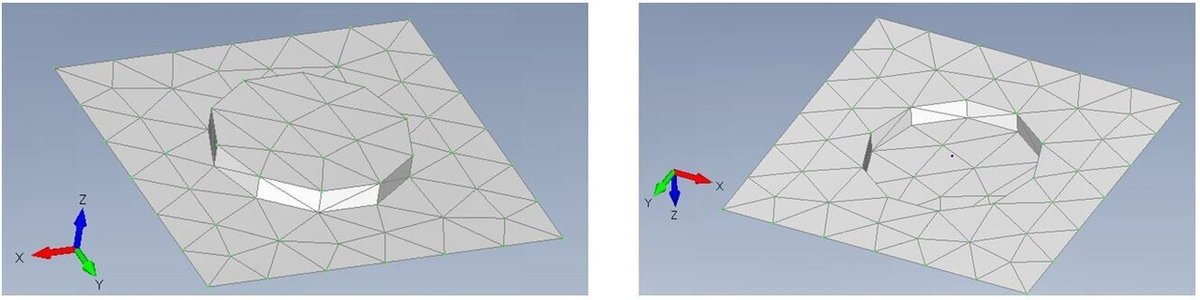
FEMモデルが欲しい方・確認したい方は下記を参照ください。
ちなみに、上記ファイル(dandd_2019_109_edit.bdf)のユニットセルのノードID(節点番号)は下図のように外周部が1~24となるように割り振っています。
ここから先は
¥ 500
この記事が気に入ったらサポートをしてみませんか?