判断推理_論理式２

このnoteでは、ワンコインで公務員試験でよく出る判断知識の問題の考え方を中心に丁寧に解説します。

特別区、地方上級、警察・消防といったやや易しめ〜基本レベルのベーシックな過去問を題材に、考え方の流れを解説していきます。
地方上級や市役所を志望する受験生におすすめです！

その他、就職や転職で非言語分野の学習をしている方にもおすすめです。

ながら勉強とか、スキマ時間勉強で判断推理を得意にしましょう！

お題

AとBの命題からCが導かれる場合、Bの「　」に入る命題として、最も妥当なのはどれか。

A「散歩が好きな人は山または海が好きである。」
B「　　　　　　　　　　　　　　　　　　　　」
C「散歩が好きな人はゲームが好きではない。」

1．ゲームが好きな人は山と海が好きである。
2．ゲームが好きな人は山または海が好きである。
3．ゲームが好きな人は山と海が好きではない。
4．ゲームが好きではない人は山または海が好きである。
5．ゲームが好きではない人は山と海が好きではない。

東京消防庁平成24年度

考え方の解説

「かつ」と「または」を含む命題の考え方

⑴　「かつ」と「または」の意味と記号の書き方

❶「pかつqである」
かつの意味は【pとqが同時に成立する】という意味です。

p　∧　q

❷「pまたはqである」
またはの意味は【pとqの少なくとも一方は成立する】という意味です。

p　∨　q

⑵　「かつ」と「または」の否定の公式(ド・モルガンの法則)

かつとまたはが入っている式の否定には懐かしのドモルガンの法則を発動させます。

❶pかつqの否定　

❷pまたはqの否定

「かつ」と「または」を含む命題の分解公式

「かつ」と「または」の式を分解するための公式があります。
これは丸暗記せよということではなく、いざ、問題で出てきた時に使いこなせるようになっていればそれでOKです。

❶　『p→q∧r』＝『p→q』、『p→r』
（ただし、『p∧q→r』は分解不可）

❷　『p∨q→r』＝『p→r』、『q→r』
（ただし、『p→q∨r』は分解不可）

分解公式を使う際は、ベン図を描きながら思い出していくのがポイントです。
❶の命題は、【pはqとrを同時に満たす部分に存在する】という意味なので、以下のようなベン図を描けます。

このベン図をみると、qとp、rとpのそれぞれの包含関係に着目することで公式のような分解が成立するというわけです。

『p→q∧r』＝『p→q』、『p→r』

同じように❷についても考えてみます。
❷の命題は、【rの中にpもqも完全に含まれる】という意味なので、以下のようなベン図を描けます。

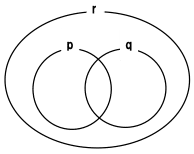
ベン図をみながら、rとp、rとqのそれぞれの包含関係に注目すると以下の公式が導かれるというわけです。

『p∨q→r』＝『p→r』、『q→r』

解説