品質管理検定 #32-05
【問5】
次の文章において、$${\boxed{\space}}$$内に入るもっとも適切なものを下欄の選択肢からひとつ選びなさい。ただし、各選択肢を複数回用いることはない。なお、解答にあたって必要であれば付表を用いよ。
ある工程の製品不適合品率は$${P_0=0.062}$$で推移していた。工場方針である品質改善に取り組んだSさんは、諸要因について改善を実施した。
① 改善実施後の工程からランダムに$${n=100}$$個のサンプルを抽出し、検査した結果$${x=2}$$個の不適合品が見つかった。改善後の工程の母不適合品率を$${P}$$とすれば、その推定値は$${\hat{P}=\boxed{(25)}}$$となる。このとき、不適合品数$${x}$$は$${\boxed{(26)}}$$分布に従う。
② 改善実施後の工程の母不適合品率が$${P{\lt}P_0}$$となっているかを検討するため、$${\boxed{(26)}}$$分布の確率関数より$${P=P_0=0.062}$$として計算すると、$${n=100}$$個中$${x=2}$$個以下となる確率は$${\boxed{(27)}}$$となる。ただし、$${n=100, P=P_0=0.062}$$のときの確率関数$${Pr(x)=\space_nC_xP_{0}^{{\space}x}(1-P_0)^{n-x}}$$の計算値を表5.1に示す。この確率の値より、有意水準5%で改善実施後の工程の母不適合品率が$${P{\lt}P_0}$$となっていると判断できる。

③ 新たに改善実施後の工程から$${n=200}$$個のサンプルをランダムに抽出し、検査した結果、$${x=6}$$個の不適合品が見つかった。正規分布近似法適用の条件$${nP_0{\ge}\boxed{(28)}}$$と$${n(1-P_0){\ge}\boxed{(28)}}$$を満足するので、
$${u_0=\cfrac{x-nP_0}{\sqrt{nP_0(1-P_0)}}=\boxed{(29)}}$$より、
$${Pr(u{\le}u_0)}$$の確率は約$${\boxed{(30)}}$$となる。
よって、有意水準5%で改善の効果はあったと判定できる。
【選択肢】
ア. -1.877 イ. 0.02 ウ. 0.0307 エ. 0.0359
オ. 0.0486 カ. 0.054 キ. 5 ク. 10
ケ. 二項 コ. ポアソン

【正解】
(25) イ. 0.02
(26) ケ. 二項
(27) オ. 0.0486
(28) キ. 5
(29) ア. -1.877
(30) ウ. 0.0307
ある工程の製品不適合品率は$${P_0=0.062}$$で推移していた。工場方針である品質改善に取り組んだSさんは、諸要因について改善を実施した。
不適合6.2%ですね。
① 改善実施後の工程からランダムに$${n=100}$$個のサンプルを抽出し、検査した結果$${x=2}$$個の不適合品が見つかった。改善後の工程の母不適合品率を$${P}$$とすれば、その推定値は「(25) 0.02」となる。このとき、不適合品数「(26) 二項」分布に従う。
製品100個中に不適合品が2個見つかっていますから、$${\frac{2}{100}=0.02}$$です。簡単に考えましょう。
この分布は「二項分布」です。何回かやってみて(サンプル数)、ある事象が発生する(不適合品)回数が従う確率分布です。二択の場合は「二項分布かも?」と思っても良いくらい。
ポアソン分布は試行回数(時間)が大きくて、発生確率が小さいときに当てはまります。
② 改善実施後の工程の母不適合品率が$${P{\lt}P_0}$$となっているかを検討するため、「(26) 二項」分布の確率関数より$${P=P_0=0.062}$$として計算すると、$${n=100}$$個中$${x=2}$$個以下となる確率は「(27) 0.0486」となる。ただし、$${n=100, P=P_0=0.062}$$のときの確率関数$${Pr(x)=\space_nC_xP_{0}^{{\space}x}(1-P_0)^{n-x}}$$の計算値を表5.1に示す。この確率の値より、有意水準5%で改善実施後の工程の母不適合品率が$${P{\lt}P_0}$$となっていると判断できる。

不適合品率は、改善実施前0.062 から 改善実施後0.020 になりました。さて、有意な差なのでしょうか?
今回の問題、数値が多いけど、そんなに必死に計算する問題じゃありません。
$${n=100}$$個中$${x=2}$$個以下となる確率は、表5.1に載っています。ここでちょっと注意。$${x=2}$$個以下ということは・・・、0個、1個、2個の3種類あります。表5.1から$${x=0,1,2}$$の確率を拾って合計します。
$${0.0017+0.0110+0.0359=0.0486}$$
確率が4.86%なので、有意水準5%で不適合品率が小さくなった、と言えます。
③ 新たに改善実施後の工程から$${n=200}$$個のサンプルをランダムに抽出し、検査した結果、$${x=6}$$個の不適合品が見つかった。正規分布近似法適用の条件$${nP_0{\ge}\boxed{(28)}}$$と$${n(1-P_0){\ge}「(28) 5」}$$を満足するので、
$${u_0=\cfrac{x-nP_0}{\sqrt{nP_0(1-P_0)}}=「(29) -1.877」}$$より、
$${Pr(u{\le}u_0)}$$の確率は約「(30) 0.0307」となる。
よって、有意水準5%で改善の効果はあったと判定できる。
せっかく100個中2個の不適合品で良くなった、と思っていたのに、200個サンプリングして不適合品が6個出たとか、ホント余計なことをしてくれます。。。まあ、何か考えがあって検査したのでしょう。無かったことにはできません。
正規分布に近似できるには、
$${nP_0{\ge}\boxed{(28)}}$$と$${n(1-P_0){\ge}「(28) 5」}$$
これが条件。よく問題に出る気がします。なんとなくキリが良い数字なので心の片隅に置いておきましょう。
計算式が載っているので、それに合わせて計算します。
$${x=6, P_0=0.062, n=200}$$です。
$${u_0=\cfrac{x-nP_0}{\sqrt{nP_0(1-P_0)}}}$$
$${=\cfrac{6-200{\times}0.062}{\sqrt{200{\times}0.062(1-0.062)}}=-1.877}$$
$${u_0=-1.877}$$ が計算できました。これからサンプル200個中不適合品6個が見つかる確率を、正規分布表から探します。
$${u_0=-1.877}$$は負の値ですけど、正規分布表は左右対称なので正の値を見ます。今回、どこを見るかというと・・・

この右側、横軸の1.877。これが、正規分布表だと、
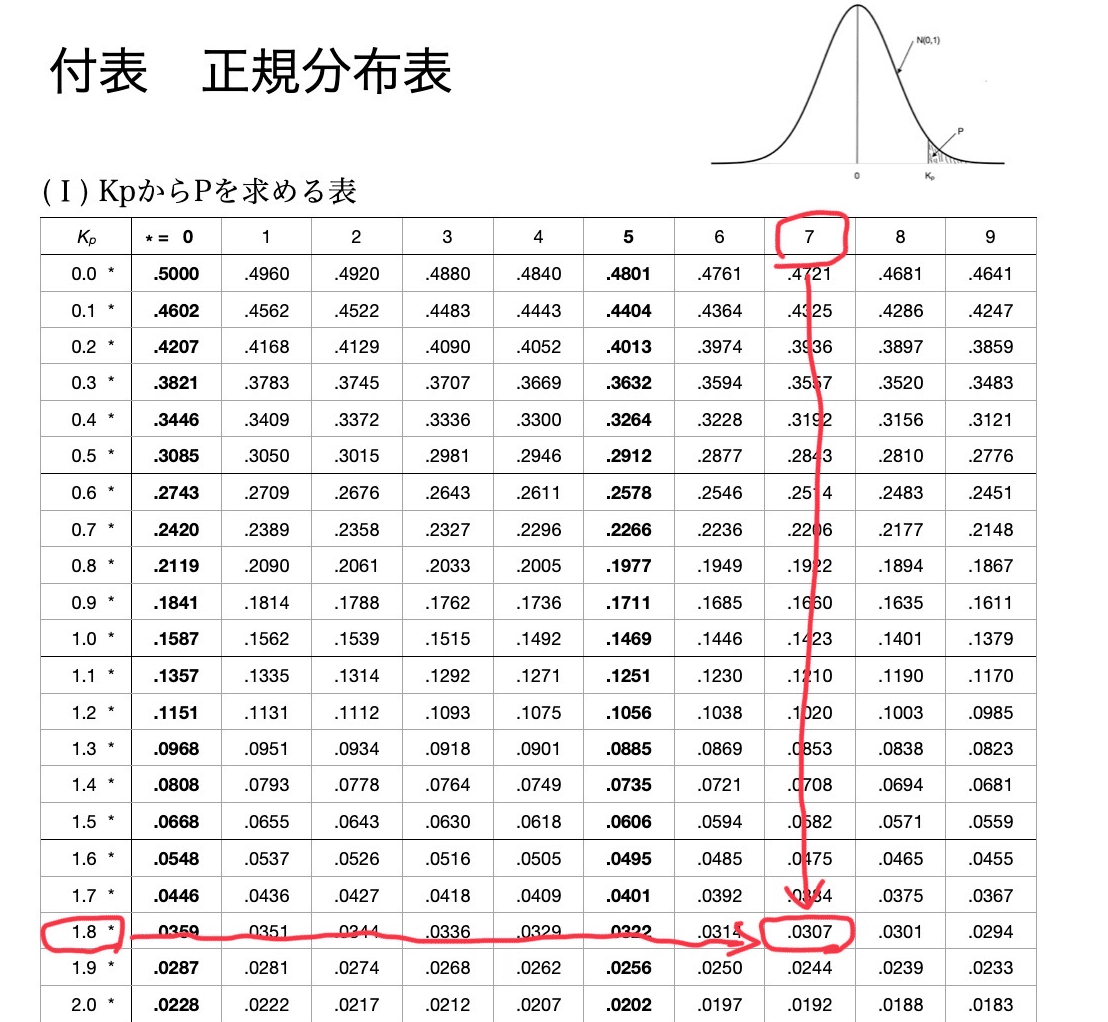
1.87のところを見ています。1.877だから1.88じゃないの?と思ったのですが、もしこれがギリギリのところだったら、数字の丸め方が有意差あり・無しを左右します。こんなときは遠慮して処理するのが良いです。1.87で大丈夫なんだからね、と。確率が小さいほど、偶然じゃないよ!という意味合いが強いですから。もし、選択肢に0.0301があったらすぐに食いついてしまうと思います😅 今回の問題で学びました。
ではー。
この記事が気に入ったらサポートをしてみませんか?
