品質管理検定 #26-07-001
[問7]
0~9の整数値をデータとする変数について、その分布を調べるため、大きさ$${n=30}$$のサンプルを収集し、度数を□で積み上げた数で表したグラフを作成する。$${\boxed{\space}}$$内に入るもっとも適切なものを下欄のそれぞれの選択肢から選びなさい。ただし、各選択肢を複数回用いることはない。
① 図7.1が得られたとき、平均値、中央値、最頻値の大きさについて、$${\boxed{(41)}}$$の関係がある。

② 図7.2の(A)〜(C)の3つのグラフが得られたとき、標準偏差の大きさについて、$${\boxed{(42)}}$$の関係がある。
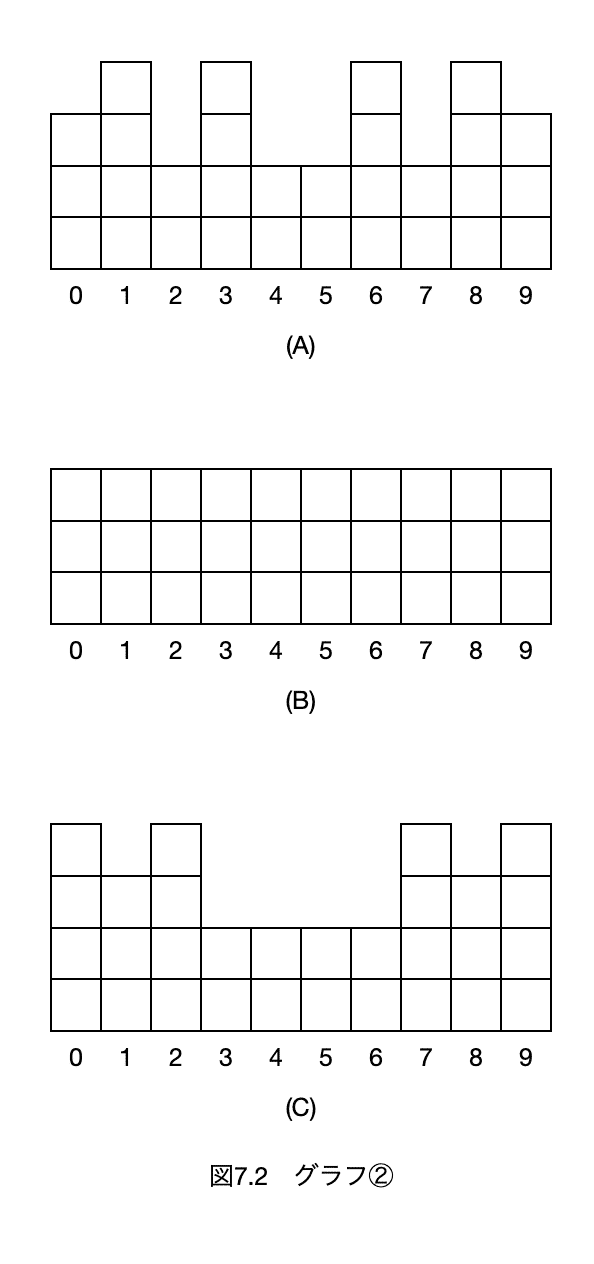
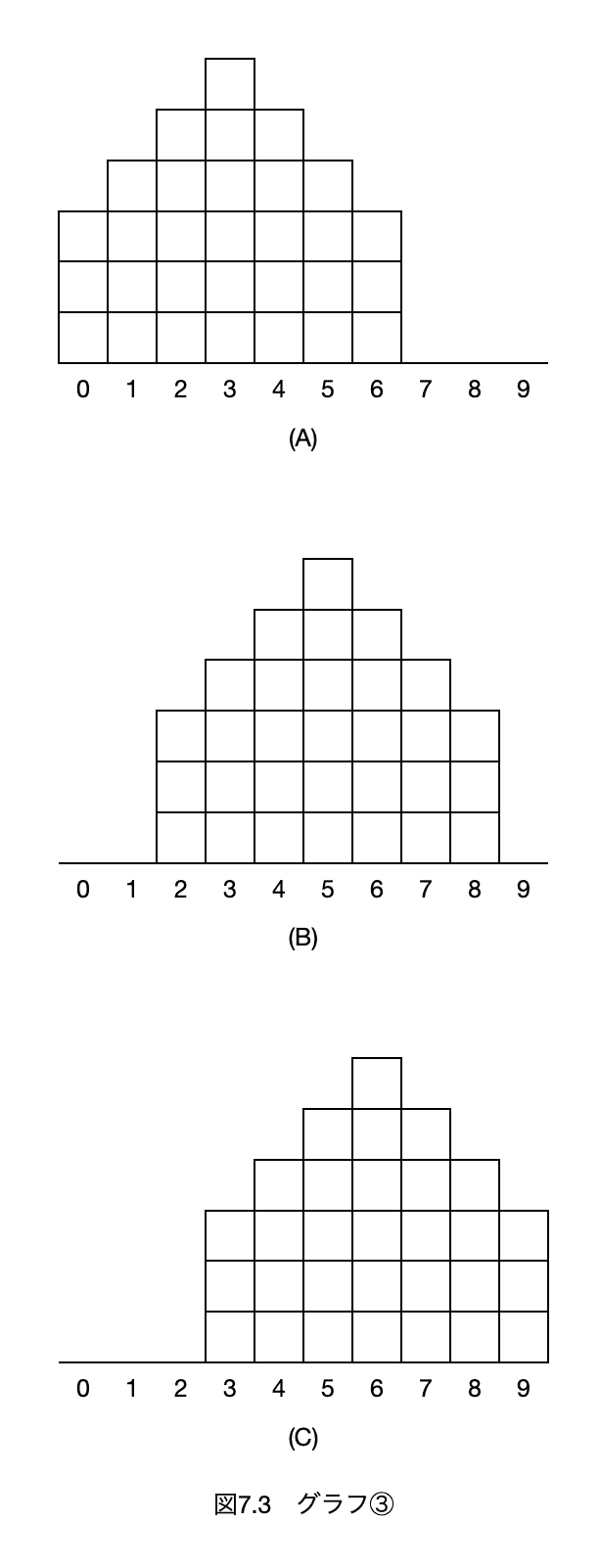
③ 図7.3の(A)〜(C)の3つのグラフが得られたとき、変動係数の大きさについて、$${\boxed{(43)}}$$の関係がある。
④ 図7.4の(A)〜(C)の3つのグラフが得られたとき、変動係数の大きさについて、$${\boxed{(44)}}$$の関係がある。

[$${\boxed{(41)}}$$の選択肢]
ア. 平均値<中央値<最頻値 イ. 平均値<最頻値<中央値
ウ. 中央値<平均値<最頻値 エ. 中央値<最頻値<平均値
オ. 最頻値<中央値<平均値 カ. 最頻値<平均値<中央値
[$${\boxed{(42)}〜\boxed{(44)}}$$の選択肢]
ア. (A)<(B)<(C) イ. (A)<(C)<(B) ウ. (B)<(A)<(C)
エ. (B)<(C)<(A) オ. (C)<(B)<(A) カ. (C)<(A)<(B)
正解
(41) オ. 最頻値<中央値<平均値
(42) ウ. (B)<(A)<(C)
(43) オ. (C)<(B)<(A)
(44) エ. (B)<(C)<(A)
この問題は、「用語の意味」と「計算方法」を知っているか。ただし計算方法が分かれば正解を導けますが、そんなに時間はないです。(41)は簡単な計算が必要です。(42)〜(44)は数字の分布から、標準偏差、変動係数の大小を感じます。
(41)
用語の意味を確認しましょう。
・平均値 ー 複数の数値データを足して、データの数で割った値。
$${\overline{x}=\cfrac{\displaystyle\sum_{i=1}^nx_i}{n}}$$
・中央値 ー データを大きさの順に並べたとき、真ん中に来る値。データが偶数個の場合は中央の2つのデータの平均値。
・最頻値 ー 複数のデータのなかで、最も個数が多い値。「モード」ともいう。
ここは見ただけじゃ分からないので計算します。
データが30個というのは問題文にあります。

□を数えれば、「最頻値」が7個ある「1」が最頻値であることはすぐに分かります。
・最頻値 = 1
データが30個なので、15番目と16番目の平均値が「中央値」になります。「0」から数えていって、15番目が「2」、16番目が「3」ですので、
・中央値 = $${\cfrac{2+3}{2}=2.5}$$
それぞれの数値に個数を掛けて、それらを合計します。90になります。データは30個ですから「平均値」は、
・平均値 = $${\cfrac{90}{30}=3}$$
最頻値<中央値<平均値 となります。
(42)
標準偏差の大きさ比べ。標準偏差の計算方法を確認しましょう。
標準偏差 = $${\sqrt{\cfrac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{x}\right)^2}{n}}=\sqrt{\displaystyle\sum_{i=1}^nx_i^2-\cfrac{\left(\displaystyle\sum_{i=1}^nx_i\right)^2}{n}}}$$
(A)〜(C)はどれも左右対称ですから、平均値は全て中央値=4.5になります。
データの数は同じですから、各データが平均値よりどれだけ離れているか、が決め手になります。
しっかり計算すれば分かりますが、それじゃあ時間がかかりすぎます。データが平均値に寄っているほうが偏差が小さい、データが平均値から離れているほうが偏差が大きいですから、
(B)<(A)<(C)
となります。微妙な感じもしますが、試験用に作ってあるので大丈夫だと思っています😅

(43)
「変動係数」です。
$${変動係数=\cfrac{標準偏差}{平均値}{\times}100}$$[%]
これ、どういうことか?というと、標準偏差って、元の数値が大きくなるのにつれて大きくなります。
いくつかのデータを、単位[g]と[kg]で扱った場合、数値だけ見れば[g]の標準偏差は[kg]の1000倍です(ただし標準偏差0の場合は同じ)。これを平均値で割ることで、単位を消して、[%]として扱います。これでデータの大きさを気にしないでばらつきの雰囲気で表せます。例えば化学実験の再現性確認では、同じ試料を5回計測して変動係数が2%以下で適合、とかやります。
この(A)〜(C)のデータの標準偏差は全て同じです。それぞれのデータの平均値からの差は(A)〜(C)はどれも同じになっています。違うのは「平均値」。「変動係数」は「標準偏差」を「平均値」で割るので、「平均値」が大きいほど、「変動係数」は小さくなります。
なので「平均値」の逆順で、
(C)<(B)<(A)
となります。

(44)
これも変動係数の大小問題。今度はデータのばらつき方が違います。
(B)は、平均値に寄っていて「標準偏差」は小さそうです。またデータが大きめなので「平均値」は大きそうです。そのため「変動係数」は小さくなります。
(A)と(C)は左右の線対称になっています。ばらつき具合は同じなので「標準偏差」は同じです。(A)は小さいデータが多いので「平均値」は小さく、(C)は大きいデータが多いので「平均値」は大きくなります。そのため「変動係数」は(A)が大きく、(C)が小さくなります。
(B)<(C)<(A)
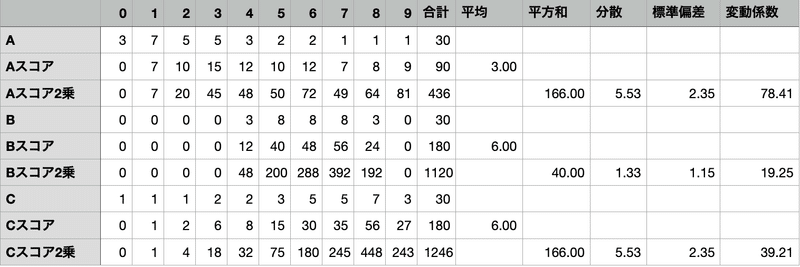
しっかり計算すれば正解が出ますが、試験時間が無くなってしまうので、標準偏差や変動係数のイメージを持っておきましょう。
ではー。
この記事が気に入ったらサポートをしてみませんか?
