数学は何の役に立つのか?

目次
1. はじめに
2. 何の役に立つ？
2.1 因数分解
2.2 場合分け
2.3 積分
2.4 抽象化
2.5 統計
2.6証明＆ゲーデルの不完全性定理
3. まとめ

1. はじめに
　「数学は何の役に立つのか？」数学がわからなかったり、勉強したくない高校生がよく先生に問う質問である。私もそれを問われた先生の一人であり、家庭教師先の生徒に「数学は何のためにやるんですか？」と聞かれた。その問いにうまく答えられなかったのが、本記事でこのテーマを選んだ理由である。
　数学が何のために役に立つのかを簡単に説明すると、想像力と論理的思考力を鍛える学問である。

2. 何の役に立つのか？
　数学が何の役に立つのかを説明するために数学の分野を複数選択した。
本稿で選択した分野が下記である。
・因数分解
・場合分け
・積分
・抽象化
・統計
・積分
・証明
これらのテーマをもとに数学と日常生活がどのように結びついているのかを説明する。

2.1因数分解
　最初に因数分解に関して説明する。大辞泉によると因数とは「一つの数や整式が、いくつかの数や整式の積の形で表せるときの、その個々の数や整式のこと。」と記載されている。つまり、因数分解とは、以下のように数字もしくは整式を掛け算に表すことである。

10 = 2×5
3xz + 2xy = x(3z +2y)
x^2+3x + 2=(x+2)(x+1)

　ここで上の２つ目の式の3xz + 2xy = x(3z +2y)という因数分解に関して考えてみる。この因数分解の作業では3xzと2xyの和はxと(3z+2y)の積と同じであるということを示している。この二つの値が同じである理由は3xzと2xyがどちらもxを含むからである。よって、因数分解の問題を解くときに求められる能力は、複数の物から共通点を探すことである。つまり、例においては3xzと2xyからxを探すという作業である。この複数のものから共通点を探す能力は、日常生活において大変重要な能力である。
　この能力が役に立つ例を一つ紹介する。初対面の人と話す状況を想像してほしい。その人と話していく中で、趣味やしゃべり方などが過去に喋ったことのある人と似ていると感じたことはあると思う。そこで過去に喋った経験をもとに「○○とか好きそう」などと推測をしたり、盛り上がりそうなエピソードを考えたりすることができる。これはまさしく、複数のものから共通点を探す能力である。
　因数分解を積の形に変えるという点に注目して考えてみる。そうすると様々な現実の事象が物事の積で構成されていることに気づく。その例として下記の数理モデルが興味深い。これは浜田宏氏が、『その問題数理モデルが解決します』で述べていた数式である。¹

やる気　＝　(価値　×　達成確率　×　価値衝動性)÷締め切りまでの時間

つまり、やる気というものが値として認識できた場合それは上のような因数の掛け算で表現できるということである。達成確率は達成しやすいほど値が大きくなる。価値衝動性は突発的に思いついた物事ほど値が小さくなる。この数式が正しいと仮定すると、達成確率、価値ともに大きく、衝動性が小さく(つまり物事を行う動機が明確)、締め切りまでの時間が短かった場合やる気は大きいいということである。この数式の正誤は賛否両論あると思うが、ここで大切なのは日常生活の感情など様々なものを積の形に表わせるということである。積の形に分解することによってわからないことを、わかる要因複数に分けて論理的な思考が可能となる。
　浜田 宏『その問題、数理モデルが解決します』ベレ出版（2018) p.95

2.2 場合分け
　数学は問題を解く時に「場合分け」というテクニックを使用する。場合分けは、複雑な構造の問題を分割して簡単な問題にすることである。代表的な場合分けを使う問題は二次関数である。二次関数は上に凸の場合と下に凸の場合でグラフの概形が大きく変わる。２次関数は上に凸、下に凸で概形が変わるため、別々に状況を考えて問題を解く。すなわち場合分けとは、複雑な事象を自分がわかる状況に落とし込んで考えることである。この能力は言うまでもなく、日常生活で役に立つ。
　この能力は自分の予定を立てるときに必要である。明日1日の予定を立てるときに一気に全部の予定を立てるのは難しい。しかし、朝の最初の行動から順を追ってわかる範囲で想像していくことで予定を立てることができる。つまり、数学とは人の想像力、論理的思考力を鍛える学問である。

2.3 積分
　積分とはある事柄の単位量当たりの増加量の値が求まっているものに対して、単位量分の増加量の和を求めることを指す。例を挙げると今回単位量を1 [s](時間)とする、その間の増加量を常に2 [m](距離)とする。すなわち単位量当たりの増加量は2 [m/s](速さ)になる。それをある単位量(10秒)の増加量の和を求めるとなると、

となり答えは20 [m]となる。これが積分である。要するに積分とは単位量当たりの何かしらの増加量の和を求めることである。人生でも同じことがいえると考えている、人生とは積分である。その場その場での努力を積み重ねていきその積み重ねが私たちの求めているものであると考えている。この積み重ねをコツコツ意識していくことが人生において大切であると私は考えている。

2.4 抽象化
　数学とは抽象化をする学問である。数字の関係性を一般化して公式化するのが数学である。例を挙げるとピタゴラスの定理である。下記のような図１の直角三角形に対して、

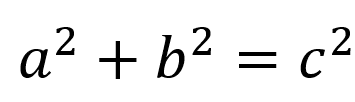
上記の関係が成立することが証明されている。

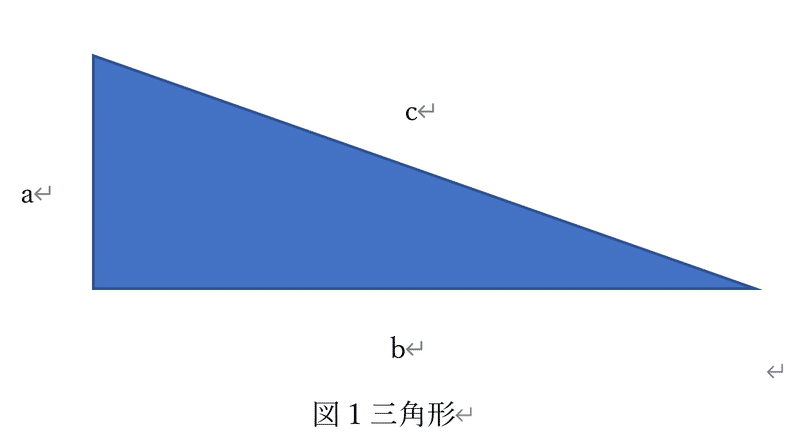
これは直角三角形の辺の長さの関係を変数を用いて抽象化したものである。このように人類が見つけたパターンをセオリーに落とし込んでいくのが数学である。パターン化することは数学以外でもスポーツやルーティン、ボケツッコミなど様々な局面でも起きる。その根本に必要な抽象化のトレーニングが数学である。

2.5　統計
　統計学とは多くのデータから自分が求めている情報を数値として取得できる。本レポートで統計学が日常生活に役に立つ例を紹介する。一般的にデータがある時に評価指標として平均値を扱うことが多い、テストの平均値や身長などである。しかし、平均値のみでデータの性質を把握するのは危険である。その例がアイスコーヒーとホットコーヒーの関係である。コンビニ定員だとしてお客さんにどちらを好むかのアンケートを100人に取ったとする。その結果50人がホット、残りの50人がアイスを希望したとする。このアンケート結果をもとに間をとってぬるいコーヒーを売れば多くの人が買ってくれるだろうか。そんなことはない、ぬるいコーヒーはだれも求めていない。この結果は統計学を学んでいなくても間違っていることはわかる。しかし世の中にはこの例に類似して数字を使って人をだまそうとしているケース、もしくは間違った決断をしていることが多い。そのような状況を避けるためにも統計学は重要な学問なのである。

2.6 証明＆ゲーデルの不完全性定理
　数学において定理を使うときは証明が必要である。証明とはこの数字の関係が必ず正しいと示すことである。数学において利用さている定理はすべて証明がされている。その中で最も衝撃を受けた定理はゲーデルの不完全性定理である。この証明はかなり難しく、詳細までは私自身も理解できていないため概要を本稿で説明する。
　ゲーデルの不完全性定理はオーストラリア・ハンガリー帝国出身の数学者のクルト・ゲーデル(Kurt Godel、1906-1978)が1930年ごろに証明した。証明されたのは、無矛盾で完全な公理系を作るのは不可能であるという命題である。
　この命題を噛み砕いて説明するとまず無矛盾とは矛盾しないということである。つまり1+1=3のような結果は出ないのである。次に完全とは、すべての真偽を証明できることである。最後に公理系とは、数学の世界のようなものである。数学は真偽が厳密な学問で、1+1=2の証明を考えたときに、数とは何かという根本的なことから考え始めるのだ。そこで最初に公理という「これは正しいと仮定してよい」というものを決めるのである。その公理をもとに様々な定理を証明していく。その公理を使って成立する法則を公理系と呼ぶ。つまり、ゲーデルの不完全性定理とはどんな公理を持ってきたとしても、矛盾せずにすべての命題を証明できる公理系は作れないということである。
　次にゲーデルの不完全性定理の証明にうつりたい。しかし、数学用語での証明は私もまだわからないため、哲学者の高橋昌一郎氏(國學院大學の高橋昌一郎教授)の『理性の限界』のゲーデルの不完全性定理の説明を参考に証明の概要を説明する。
　
　ある島の中に真の命題しか言わない「ナイト(騎士)」と、偽の命題しか言わない「ネイブ(ならず者)」がいるとする。この島が公理系である。ナイトの発言の例としては「1+1=2」、ネイブの例は「1+1=3」である。島の住人Xを正しいとその公理系の公理を用いて証明できた場合その人はナイトであると証明できたことになる。このように証明できたナイトをナイト会員とする、逆にXの発言が偽であると証明できた場合そのXをネイブ会員とする。それではXが「私はナイト会員ではない。」と発言したとする。Xはナイトであるか、ネイブであるか。答えはナイトである。なぜならネイブはナイト会員になることはないため、「ナイト会員ではない。」という発言はできない。それでは、この「私はナイト会員ではない。」と発言した人をナイト会員にするために証明しようとする。しかしそれは証明できてはならない。なぜなら、このXがナイト会員になってしまった場合、発言が正しいということになり、ナイト会員であるのにもかかわらず、「ナイト会員ではない。」と発言をしてしまうからである。よって、島の中のナイトすべてをナイト会員にすることは不可能、つまりすべての命題を証明するのは不可能であるということが証明されてしまったのである。これがゲーデルの不完全性定理の証明の概要である。

　このゲーデルの不完全性定理は哲学や宗教に大きな影響を与えた。なぜなら、どんな神様でも公理系理論の下ではすべての真偽を示すことができないため、全知全能の神はいないことを証明してしまったからである。このように数学は科学だけでなくほかの学問にも大きな影響を与えるのである。

3. まとめ
　数学は何の役に立つのかという主題に沿って、数学の考え方が現実世界の役に立つことを述べた。因数分解は要因分析、場合分けは想像力、積分は積み重ね、抽象化はセオリー、統計は客観的判断、証明は数学の絶対的真偽、そして科学以外にも役に立っている。まとめると、数学を学んでいくことで想像力や論理的思考力が鍛えられることができる。

4. 参考文献
浜田 宏,『その問題、数理モデルが解決します』.ベレ出版 (2018)
高橋 昌一郎,『理性の限界――――不可能性・不確定性・不完全性』.講談社 現代新書(2008)
西成 活祐,『とんでもなく役に立つ数学』.角川ソフィア(2014)