
自然科学モデル:フラクタル
フラクタルについて
マンデルブロのフラクタルは、ベノワ・マンデルブロ(Benoit Mandelbrot)というフランスの数学者が命名した幾何学の概念です。 彼は、数学について図形(フラクタル図形)を用いて視覚的に問題を解くと言うアプローチを実践し、これからフラクタルを導入しました。 マンデルブロのフラクタルは、数学、物理学、生物学など多くの分野で応用があります。特に、自然界の複雑な構造やパターンを理解するためのモデルとして、フラクタル幾何学は広く利用されています。ここから、CG、遺伝子工学、形状解析などの発展に貢献しています。
フラクタルは、繰り返しのパターンを持つ複雑な幾何学的形状であり、「自己相似性(全体が部分に似ている)」を特徴としています。 彼の言葉によると、「無限の不思議は、単純な法則を繰り返し生み出される」ものとフラクタルに対して述べています。 マンデルブロのフラクタルは、その自己相似性が非常に複雑で美しいことで知られています。
マンデルブロ集合
マンデルブロ集合は、複素数平面上の点が発散するかどうかによって定義されます。
具体的には、以下の漸化式に基づいて評価されます。

ここで、ZとCは複素数であり、nは0から始まる整数です。 最初は𝑍0=0Z0=0とし、Cは複素数平面上の点です。
この漸化式を繰り返し適用していくと、Zの値は発散するか収束するかが決まります。
発散しない点(すなわち、絶対値が無限大にならない点)をマンデルブロ集合の一部とします。
マンデルブロ集合は、以下の手順で描画することができます。
複素数平面上の各点Cについて、上記の漸化式を繰り返し適用します。
点Cがマンデルブロ集合に属するかどうかを判断します。これは、Zの絶対値がある閾値(通常は2)を超えない場合、収束とみなし、属すると判断します。ただし、繰り返し回数には上限(例えば1000回)を設けます。
マンデルブロ集合に属する点は黒で塗り、属さない点はその発散速度に応じて異なる色で塗ります。
マンデルブロ集合を描画するには、複素数平面上の各点Cについて、漸化式を繰り返し適用し、その点がマンデルブロ集合に属するかどうかを調べます。
集合に属する点は黒で塗り、属さない点はその発散速度に応じて異なる色で塗ります。 このようにして描かれたマンデルブロ集合の画像は、非常に美しいフラクタル図形となります。
マンデルブロ集合に属するCを数値的に探し出す方法
マンデルブロ集合に属するCを数値的に探し出す方法は、各点Cについて発散の有無を調べることです。以下は、マンデルブロ集合に属するCを探し出すための基本的なアルゴリズムです。
複素数平面を選択した範囲でグリッド状に区切ります。 例えば、実部が -2 から 1、虚部が -1.5 から 1.5 の範囲でグリッドを作成します。
グリッド上の各点Cについて、次の漸化式を繰り返し適用します: Zn+1 = Zn^2 + C。最初は、Z0 = 0 とします。
点Cがマンデルブロ集合に属するかどうかを判断します。 Zの絶対値がある閾値(通常は2)を超えない場合、収束とみなし、属すると判断します。
ただし、繰り返し回数には上限(例えば1000回)を設けます。
上記の手順で、マンデルブロ集合に属するCを特定できます。
Python codeの例1
以下は、Pythonを使ってマンデルブロ集合に属するCを探し出す例です。
import numpy as np
def mandelbrot(c, max_iter=1000):
z = 0
for n in range(max_iter):
z = z*z + c
if abs(z) > 2:
return False # 発散
return True # 収束
# 複素数平面の範囲とグリッドの解像度を設定
real_min, real_max = -2, 1
imag_min, imag_max = -1.5, 1.5
resolution = 500
# グリッド上の各点について、マンデルブロ集合に属するか調べる
real_values = np.linspace(real_min, real_max, resolution)
imag_values = np.linspace(imag_min, imag_max, resolution)
belongs_to_mandelbrot = []
for imag in imag_values:
for real in real_values:
c = complex(real, imag)
if mandelbrot(c):
belongs_to_mandelbrot.append(c)
# マンデルブロ集合に属するCのリスト
print(belongs_to_mandelbrot)フラクタル画像を表画するには、以下のコードを使用します:
import matplotlib.pyplot as plt
mandelbrot_image = np.empty((resolution, resolution))
for i, imag in enumerate(imag_values):
for j, real in enumerate(real_values):
c = complex(real, imag)
mandelbrot_image[i, j] = mandelbrot(c)
# フラクタル図形を描画
plt.imshow(mandelbrot_image.T, cmap='inferno', extent=[real_min, real_max, imag_min, imag_max])
plt.xlabel("Real")
plt.ylabel("Imaginary")
plt.title("Mandelbrot Set")
plt.colorbar()
plt.show()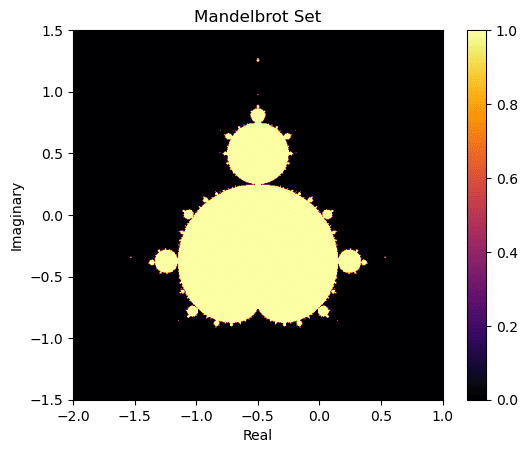
Python codeの例2
import numpy as np
import matplotlib.pyplot as plt
def mandelbrot(arr, width, height, xmin, ymin, xcoef, ycoef, maxIt):
for ky in range(height):
cy = ycoef * (height - ky) + ymin
for kx in range(width):
cx = xcoef * kx + xmin
c = complex(cx, cy)
z = complex(0.0, 0.0)
flag = True
for i in range(maxIt):
count = i
z = z * z + c
if abs(z) >= 2.0:
flag = False
break
if flag:
arr[ky, kx] = (255, 255, 255)
else:
# カラーの計算方法を追加
color = 255 * count // maxIt
arr[ky, kx] = (color, color, color)
# 画像サイズとパラメータ設定
width, height = 800, 800
xmin, ymin = -2, -2
xmax, ymax = 2, 2
xcoef = (xmax - xmin) / width
ycoef = (ymax - ymin) / height
maxIt = 256
# 画像データを格納する配列を準備
image_data = np.empty((height, width), dtype=np.dtype(('u1', 3)))
# マンデルブロ集合を計算
mandelbrot(image_data, width, height, xmin, ymin, xcoef, ycoef, maxIt)
# 画像を表示
plt.imshow(image_data)
plt.show()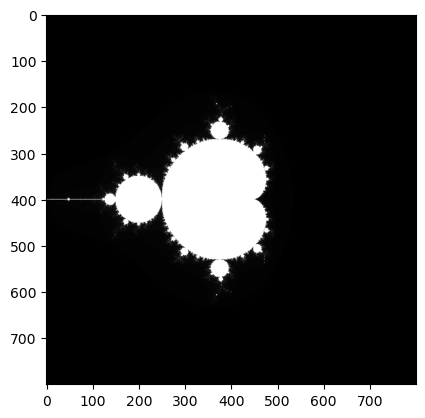
こちらのコードは、以下の書籍を参考に作成しました:
Pythonコンピュータシミュレーション入門 人文・自然・社会科学の数理モデル
バーンスレイのシダ(Barnsley fern)
バーンスレイのシダ(Barnsley fern)は、イギリスの数学者マイケル・バーンスレイ(Michael Barnsley)によって提案されたフラクタル図形です。このフラクタル図形は、自然界におけるシダの葉に非常に似た形状を持っており、フラクタル幾何学の応用例として知られています。
バーンスレイのシダは、確率的イテレーティブ関数システム(IFS: Iterated Function System)と呼ばれる手法を用いて生成されます。IFSは、複数のアフィン変換(線形変換と平行移動の組み合わせ)を確率的に適用することで、フラクタル図形を生成します。
バーンスレイのシダを生成するためには、以下の4つのアフィン変換とそれぞれの確率が与えられています。
f1(x, y) = (0, 0.16 * y) (確率: 1%)
f2(x, y) = (0.85 * x + 0.04 * y, -0.04 * x + 0.85 * y + 1.6) (確率: 85%)
f3(x, y) = (0.2 * x - 0.26 * y, 0.23 * x + 0.22 * y + 1.6) (確率: 7%)
f4(x, y) = (-0.15 * x + 0.28 * y, 0.26 * x + 0.24 * y + 0.44) (確率: 7%)
*f1 = シダの茎; f2 = 連続する小さい葉; f3 = 左側の大きな葉; f4 = 右側の大きな葉
このアフィン変換を確率的に繰り返し適用することで、バーンスレイのシダのフラクタル図形が生成されます。最初に任意の点(例えば、原点)を選び、選択された確率に基づいてランダムにアフィン変換を適用し、新しい点を計算します。これを繰り返すことで、次第にシダの葉に似たフラクタル図形が現れます。
バーンスレイのシダは、フラクタルが自然界の形状やパターンを表現する力を示す良い例です。また、IFSを用いたフラクタル生成手法は、画像圧縮やコンピュータグラフィックスなどの応用分野でも利用されています。
バーンスレイのシダを描画するPythonコードの例
以下は、バーンスレイのシダを描画するPythonコードの例です。
import numpy as np
import matplotlib.pyplot as plt
import random
# アフィン変換関数
def f1(x, y):
return 0, 0.16 * y
def f2(x, y):
return 0.85 * x + 0.04 * y, -0.04 * x + 0.85 * y + 1.6
def f3(x, y):
return 0.2 * x - 0.26 * y, 0.23 * x + 0.22 * y + 1.6
def f4(x, y):
return -0.15 * x + 0.28 * y, 0.26 * x + 0.24 * y + 0.44
# 確率に基づいてアフィン変換関数を選択
def get_transform(prob):
if prob < 0.01:
return f1
elif prob < 0.86:
return f2
elif prob < 0.93:
return f3
else:
return f4
# バーンスレイのシダを描画
def draw_barnsley_fern(iterations):
x, y = 0, 0
x_values, y_values = [x], [y]
for _ in range(iterations):
transform = get_transform(random.random())
x, y = transform(x, y)
x_values.append(x)
y_values.append(y)
plt.scatter(x_values, y_values, s=0.1, c='g')
plt.axis('equal')
plt.show()
# 描画
iterations = 100000
draw_barnsley_fern(iterations)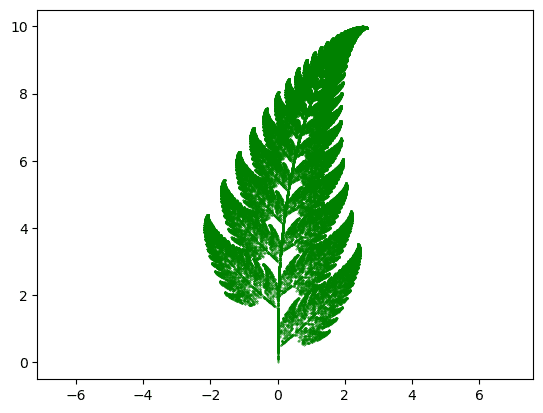
バーンスレイのシダは、フラクタル幾何学の美しい例であり、自然界に見られるシダの葉の形状を驚くほど正確に再現しています。このフラクタル図形は、確率的イテレーティブ関数システム(IFS)を用いて生成されます。
参考&おすすめ書籍

Pythonコンピュータシミュレーション入門 人文・自然・社会科学の数理モデル
良質な記事をお届けするため、サポートしていただけると嬉しいです!英語論文などの資料取り寄せの費用として使用します。
