ファイナンス機械学習：　分数差分をとった特徴量　非整数差分オペレータ

Dean＠Edinburgh

　時系列の分析には、非定常な時系列を定常時系列に変換する差分は不可欠であるが、整数差分は過去の履歴を削り、シグナルを弱めてしまう。
　可能な限りに長期履歴を保持しながら、価格時系列を定常化する最小の差分を行うために、差分オペレータを非整数次に一般化する。バックシフトオペレータ$${B}$$は、$${k}$$を正の整数$${k}$$として、実数値を取る特徴行列$${X_t}$$に対し、$${B^k X_t = X_{t-k},k \ne 0}$$と変換するとする。
　$${(1-B)^2=1-2B+B^2}$$、$${B^2X_t=X_{t-2}}$$となるから
$${(1-B)^2X_t=X_t -2X_{t-1} + X_{t-2} }$$。

　$${B}$$は、差分オペレータであるから十分小さいとし、任意の実数$${d}$$について、$${(1-B)^d}$$をマクローリン展開をすると、
$${(1-B)^d=\displaystyle{\sum^{\infty}_{k=0} \frac{\Pi^{k-1}_{i=0}(d-i)}{k!}(-B)^k }}$$と書ける。

差分と長期メモリー

　$${(1-B)^d}$$の展開式を$${X_t}$$に作用すると、
$${\displaystyle{ (1-B)^dX_t=\sum^{\infty}_{k=0} \frac{\Pi^{k-1}_{i=0}(d-i)}{k!}(-B)^k X_t }}$$
$${\displaystyle{ = X_t - d X_{t-1} + \frac{d(d-1)}{2!}X_{t-2} - \dots }}$$ $${\displaystyle{+(-1)^{k} \frac{\Pi^{k-1}_{i=0}(d-i)}{k!}X_{t-k} \dots }}$$。
　各係数を重みとして、$${\displaystyle{ \{w_k\}=\{ 1, -d, \frac{d(d-1)}{2!}, \dots, (-1)^{k}\frac{\Pi^{k-1}_{i=0}(d-i)}{k!}, \dots \} }}$$とすれば、
$${\tilde{X_t}=\displaystyle{\sum^{\infty}_{k=0} w_k X_{t-k}}}$$
　$${d}$$を正整数$${n}$$とすると、二項定理により、
$${(1-B)^n=\displaystyle{\sum^{n}_{k=0}\begin{pmatrix} n \\ k \\ \end{pmatrix} (-B)^{k}}}$$
で、上限がnと決まるから、n以降のメモリーは失われていると考えられる。
$${n=1}$$の時、$${(1-B)X_t=X_t - X_{t-1}}$$のリターンである。

反復処理による推定

$${(1-B)^d}$$から来る時系列の各時点の重み$${w_k}$$の最初の項が$${w_0=1}$$であるから、
$${\displaystyle{\frac{w_{k}}{w_{k-1}}=-\frac{d-k+1}{k}=1-\frac{d+1}{k}}}$$と書ける。
$${k}$$は１以上の整数であるから、$${d<-1}$$では、過去の特徴量の重みが現在の特徴量への重みよりも大きくなることから、現実的ではない。$${d=-1}$$では、重みは全期間を通じて同じになる。
よって意味のある$${d}$$の下限は$${-1<d}$$であり、$${-1 < d < 0}$$では重みは符号を変えることなくゼロに収束し、$${d>0}$$では$${w_k}$$は符号を変えながらゼロに収束する。収束の速度は$$d$$が大きくなると遅くなり、振り幅も大きくなる。
　これを以下のコードを用いてグラフにする。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

%matplotlib inline

def getWeights(d, size):
    w=[1.]
    for k in range(1,size):
        w_ = -w[-1]/k*(d-k+1)
        w.append(w_)
    w=np.array(w[::-1]).reshape(-1,1) #配列順を逆にして返している
    return w

def plotWeights(dRange, nPlots, size):
    w=pd.DataFrame()
    for d in np.linspace(dRange[0], dRange[1], nPlots):
        w_=getWeights(d, size = size)
        w_ = pd.DataFrame(w_, index = range(w_.shape[0])[:: -1], columns = [d])
        w=w.join(w_, how = "outer")
    ax = w.plot(figsize=(10,8))
    ax.legend(loc='lower right'); plt.show()
    return
plotWeights(dRange=[-1,1],nPlots=11,size=6)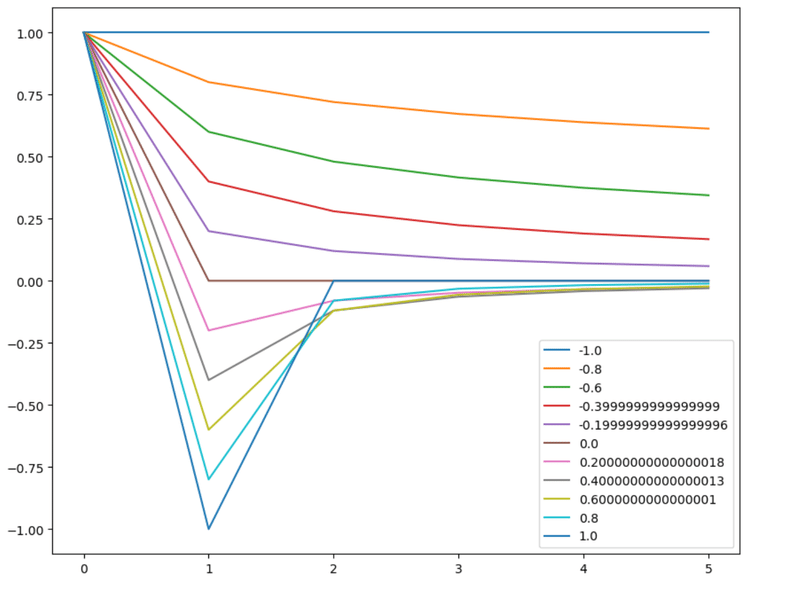
分数差分による各時点への重み　-1<d<=1
plotWeights(dRange=[1,5],nPlots=5,size=10)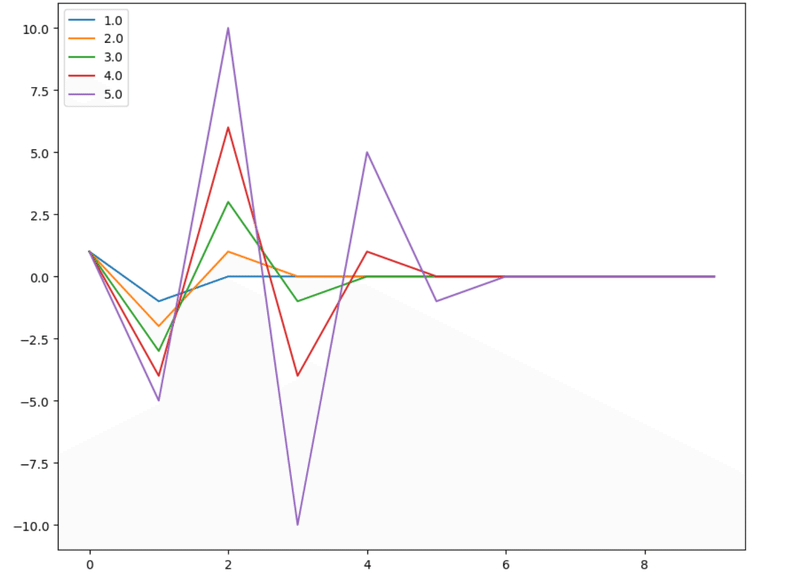
分数差分による各時点への重み　d=[1,5]

重みの意味ある領域が$${[-1,1]}であることから、$${d}$$は、$${-1\le d \le 2}$$であるべきである。

この記事が気に入ったらサポートをしてみませんか？