機械学習：クラスタリング　クラスタの数

エルボー法

クラスタリングにおいて、教師無しの学習となると正解がなく、当然ながら、最適なクラスタの数も未知である。

　クラスタ内誤差平方和をクラスタ数毎にプロットして、それ以上に改善されない数、もしくはある閾値に達したらその数を最適とするエルボー法がある。この方法は、以下のように実装される。

SSE = []
for i in range(1, 11):
    km = KMeans(n_clusters=i, init='k-means++', n_init=10, 
                max_iter=300, random_state=0)
    km.fit(X)
    SSE.append(km.inertia_)
    
plt.plot(range(1, 11), SSE, marker='o')
plt.xlabel('Number of clusters')
plt.ylabel('Distortion')
plt.tight_layout()
plt.show()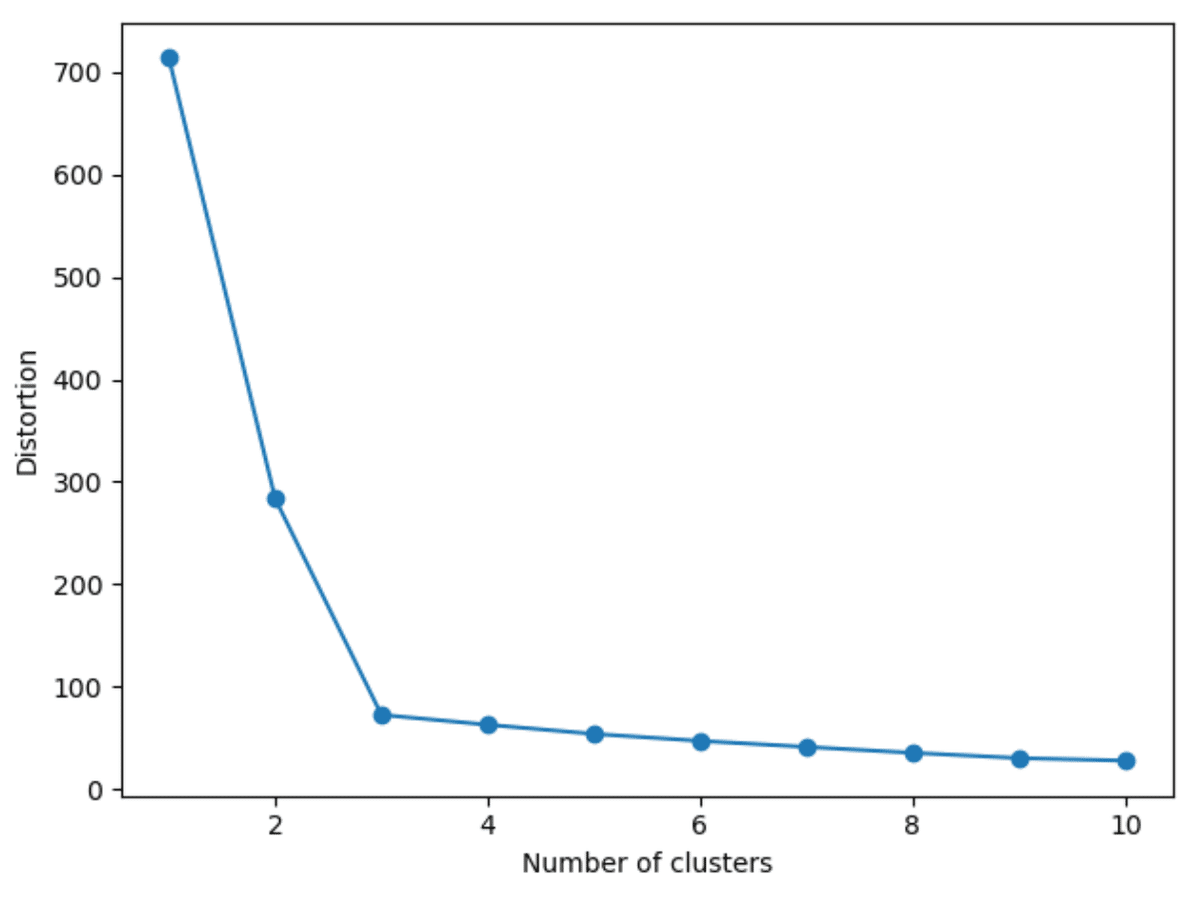

エルボー法

　これによって、$${K=3}$$が最適なクラスタ数と言える。

シルエット分析

　クラスタ内距離とクラスタ間距離を比較するシルエット係数を導入し、データ点がどの程度密にクラスタ化されているかを可視化する。この係数は、k-means法だけでなく、他のクラスタリングアルゴリズムに使用できる。
　クラスタの凝縮度である内距離$${a^{(i)}}$$は、クラスタ$${i}$$に属する点$${\bf{x}^{(i)}}$$と、クラスタ$${i}$$内全てのデータ点との平均距離である。
　クラスタ$${i}$$に最も近いクラスタからの乖離度$${b^{(i)})}$$は、クラスタ$${i}$$に属する点$${\bf{x}^{(i)}}$$と最も近いクラスタ内の全てのデータ点との平均距離で、$${a^{(i)})}$$と$${\bf{x}^{(i)}}$$の比較がシルエット係数となる。
$${S^{(i)}=\displaystyle{\frac{b^{(i)}-a^{(i)}}{max\{b^{(i)},a^{(i)}\}}}}$$
　シルエット係数は$${[-1,1]}$$の値を取り、$${S^{(i)}=-1}$$では全くクラスタ化されておらず、$${1}$$に近づくにつれクラスタ化が進んでいる。
　このシルエット係数は、scikit-learnのmetricモジュール中のsilhouette_samplesクラスで呼び出せる。

import numpy as np
from sklearn.metrics import silhouette_samples

km = KMeans(n_clusters=3, init='k-means++', n_init=10, max_iter=300,
            tol=1e-04,random_state=0)
y_km = km.fit_predict(X)

sil_vals = silhouette_samples(X, y_km, metric='euclidean')

sil_valsには、全てのデータ点のシルエット係数が入っている。これをクラスタ別にソートして横積みグラフで出力する。

from matplotlib import cm
cl_labels = np.unique(y_km)
n_cl = cl_labels.shape[0]
y_ax_lower, y_ax_upper = 0, 0
yticks = []
for i, c in enumerate(cluster_labels):
    c_sil_vals = sil_vals[y_km == c]
    c_sil_vals.sort()
    y_ax_upper += len(c_sil_vals)
    col = cm.jet(float(i) / n_cl)
    plt.barh(range(y_ax_lower, y_ax_upper), c_sil_vals, height=1.0, 
             edgecolor='none', color=col)

    yticks.append((y_ax_lower + y_ax_upper) / 2.)
    y_ax_lower += len(c_sil_vals)
    
sil_avg = np.mean(sil_vals)
plt.axvline(sil_avg, color="red", linestyle="--") 

plt.yticks(yticks, cluster_labels + 1)
plt.ylabel('Cluster')
plt.xlabel('Silhouette coefficient')
plt.tight_layout()
plt.show()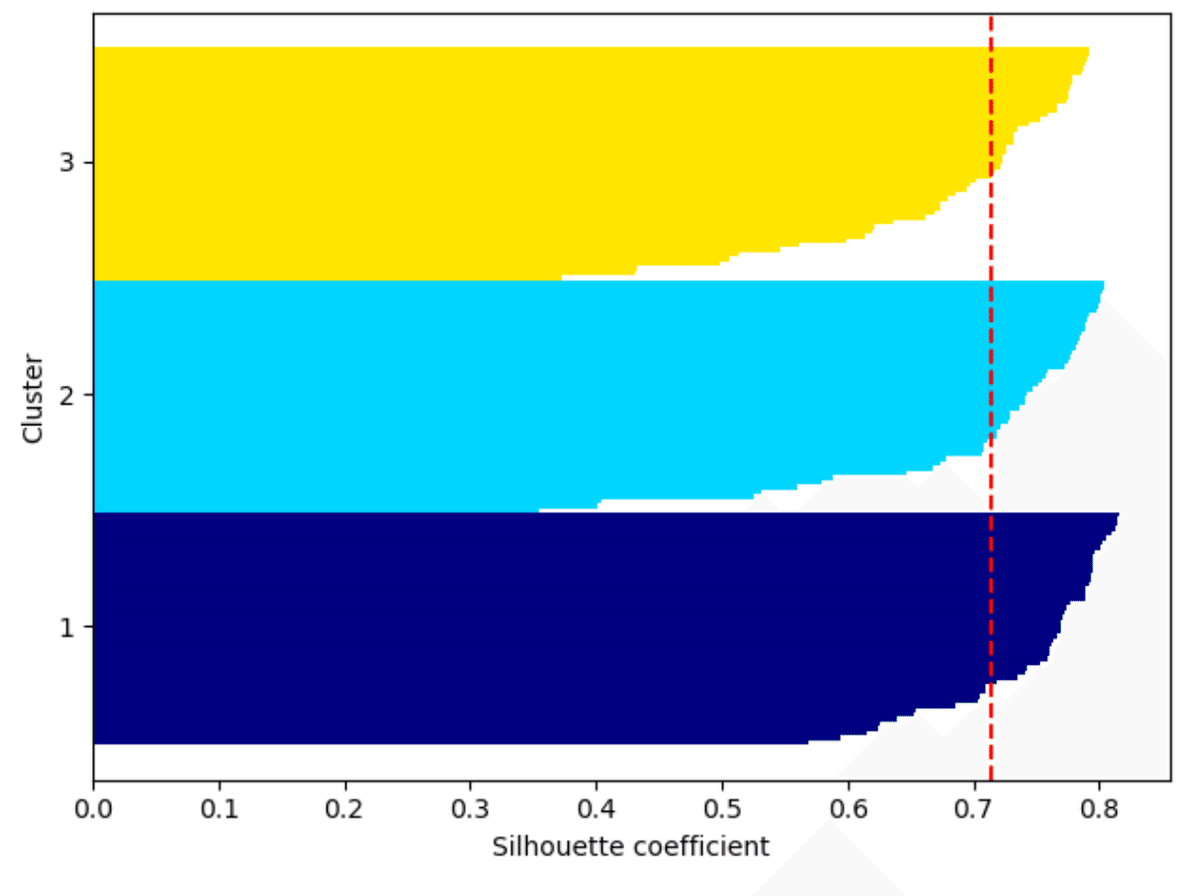

シルエット係数

　赤の点線は、全シルエット系数の平均値で、$${0.71}$$となり、よくクラスタリングされていると言える。