【確率分布・正規分布】〈7〉 標準正規分布

　【統計】分野について解説します。
新課程では必須の学習内容ですが、まだまだ高校での指導方法が確立していないんだよね。では、端的に、わかりやすく、解説していきましょう。
　ここからは、分布とその性質です。この節は、〈標準正規分布〉です。

〈標準正規分布〉

・反復試行・検査では、「二項分布」となることは前節で学びました。
十分大きな回数を繰り返すと、「正規分布」に近似でき、N(m、σ) と表されます。
・まず、題意を「二項分布」と捉え、
　平均         ：m = np
　分散         ：σ^2 = np(1-p)
　標準偏差：σ = √np(1-p)
　と、各指標を順に求め、十分大きな回数であれば「正規分布」と考えられ（近似できて）、N(m、σ) と表すことができます。最後に、
　Z = (X-m)/σ
と変換することで、「標準正規分布」N(0、1) に従うことになります。
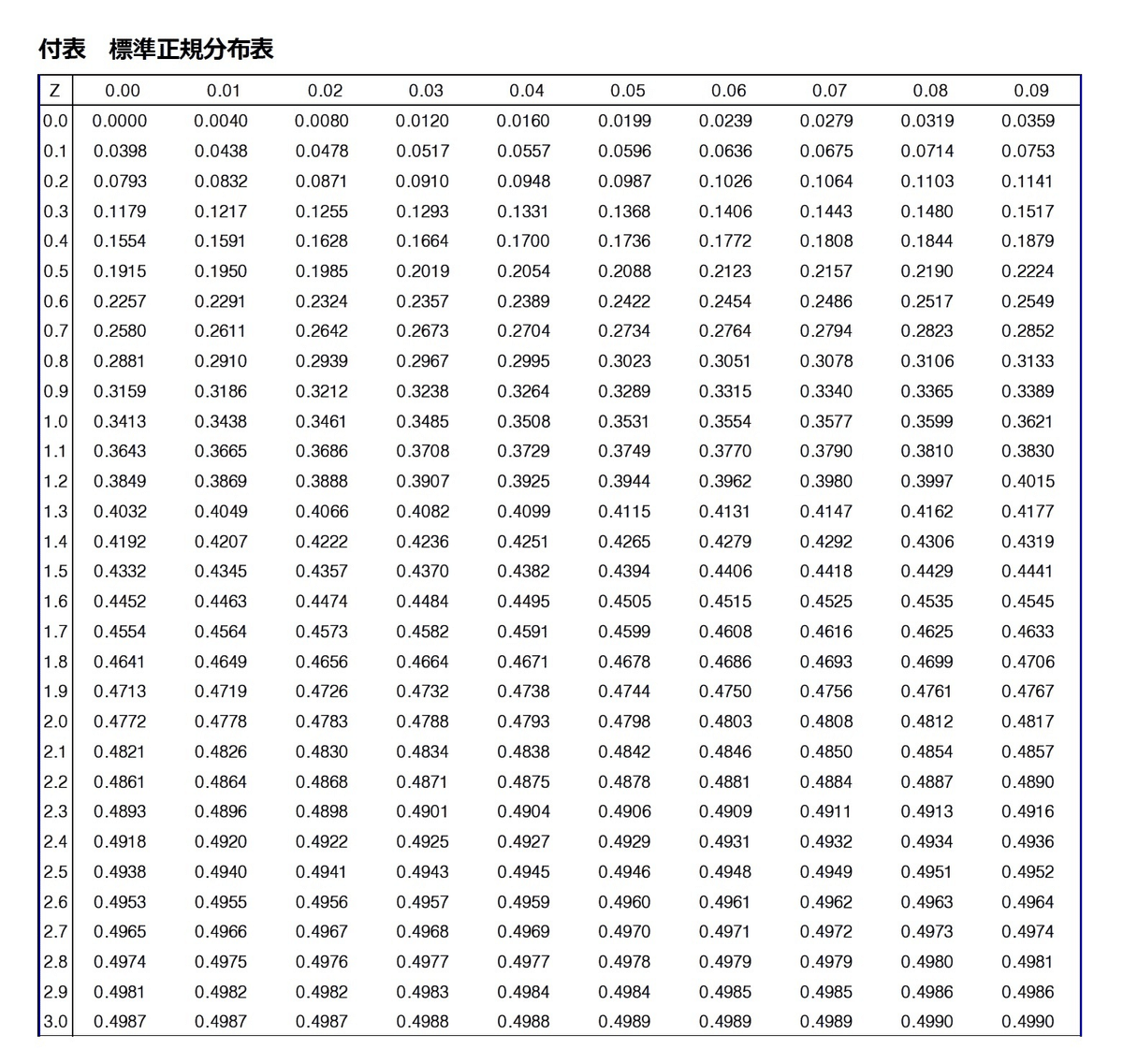
・「標準正規分布」は、面積が１である分布で、富士山型をしています。
、下の〈別表〉のように、平均値からある値までの面積＝分布上の量＝確率となります。

標準正規分布の確率変数曲線

［例題］（前節と同じ例題）
・赤玉３個、白玉２個が入っている袋から１個取り出し、色を確認してから元に戻します。この試行を100回繰り返します。（反復試行）
・赤玉の出る回数をXとして、回数Xの確率分布を考えていきます。

［解法］
① ターゲット事象（赤玉が出る）確率： p = 3/5
② 排反事象（白玉が出る）確率            ： 1-p = 2/5　
③ 「二項分布」となれば、n=100、 p = 3/5、 1-p = 2/5 なので、
　平均        ：m = np = 100*3/5 = 60（回）
　分散        ：σ^2 = np(1-p) =  100*3/5*2/5 = 24 
　標準偏差：σ = √np(1-p) = √24 = 2√6（回）
④ この場合、回数が100回と多いので、「正規分布」に従うと考えられます。N(60、 2√6) の正規分布です。
⑤ 多くの場合、回数Xを、以下の式で変換します。
　Z = (X-m)/σ
　これで、回数Xを変数とする「正規分布」は、Zを変数とする「標準正規分布」N(0、1) に従うようになります。
⑥ 例えば、60回から70回でる確率は、どれくらいなのでしょうか？
　Z = (65-60)/2√6) = 2.04
　P(60<X<65)＝P(0<Z<2.04) = 0.4793
⑦ 例えば、70回以上でる確率は、どれくらいなのでしょうか？
　Z = (80-60)/2√6) = 4.08
　P(60<X<70)＝P(0<Z<2.04) = 0.4793

［Method］
・「正規分布」
　例えば、上の例題では、N(60、 2√6) の正規分布に従うと考えます。
ここで扱う、60と 2√6には、単位(回)が付いていますね。統計では、平均値ｍ、標準偏差σ が大切な数値であることが、ここからもうかがい知れます。
・「標準正規分布」
　この施行を繰り返せば、だいたい60回赤玉が出るのですが、、、、
では、
では、90回出る確率と10回出る確率とは、同じなのでしょうか？

〈別表〉

標準正規分布表