
特殊な積分
こんにちは。今回は特殊な積分の話です。これも「型」で覚えるものですね。
分数関数は分母を因数分解→部分分数分解、ここで分母がすでに一次関数のときは分子が定数の形になるように変形します。そこから積分すると安易に計算ができます。ちなみに、例外として(微分後)/(微分前)になっているときは、真数が微分前の関数の絶対値となる自然対数になります。と、このように文面で書いてきましたがやっぱり実際に演習した方が確実に覚えます。
さて、本当にきつくて実用性があるのは
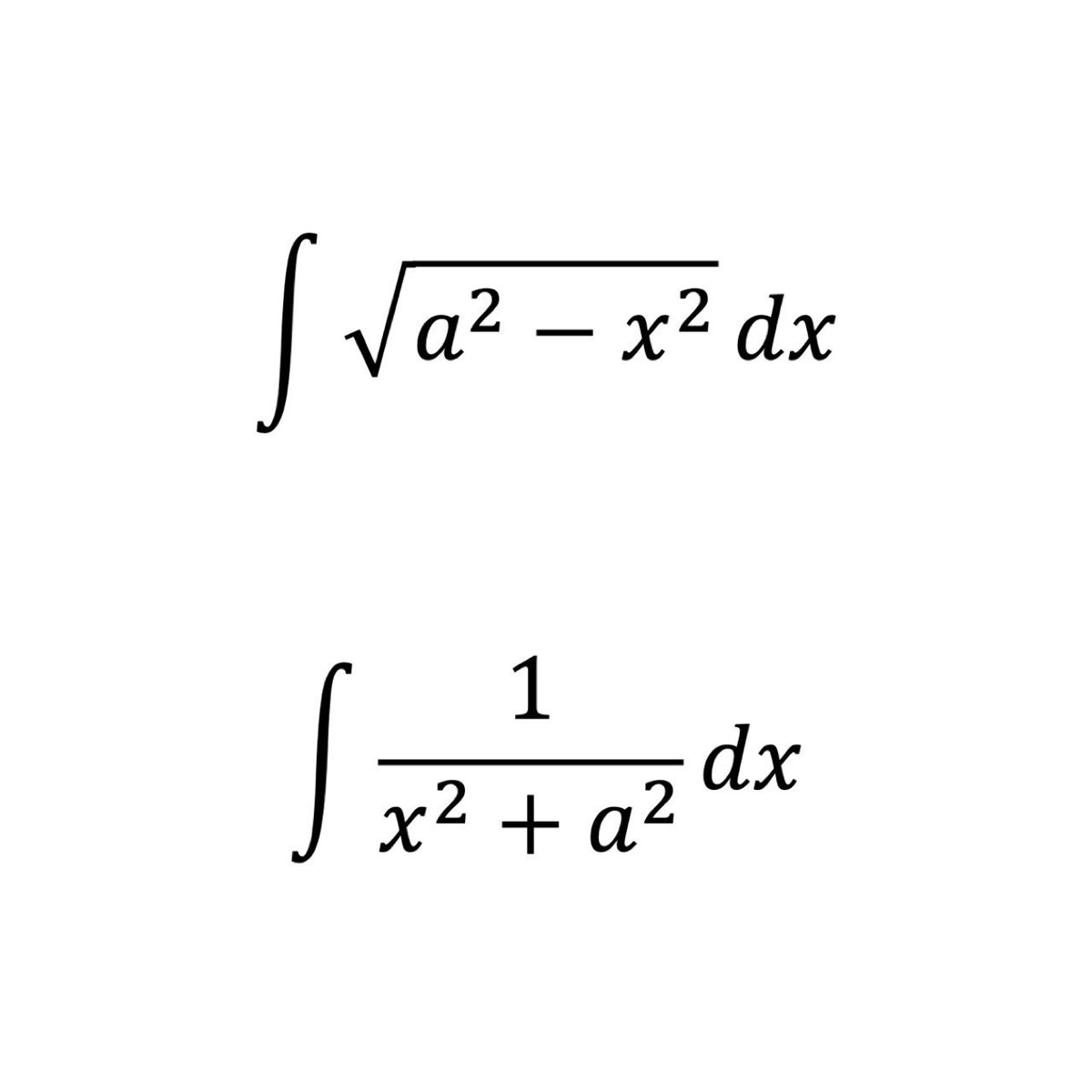
の積分です。前者はx=a sintと、後者はx=a tantと置換すると三角関数の式から簡単に変形できます。これはきついですがとても有用な式です。ぜひ解き方を覚えましょう。
定積分には何分の1公式なるものがありますが正直言って覚えなくていいです。前回・今回で書いた式の理解の方を優先して下さい。
このほかにももっと複雑な積分があり、どれも固有(とはいえ基本には則ってはいる)の解き方をします。これらはコメントでくるか受験問題を解くコーナーとかができたらやるかもしれません。次回は面積・体積の話です。よろしくお願いします。



clue zemi の詳細・お問い合わせはこちら↓
この記事が気に入ったらサポートをしてみませんか?





