
5.市場均衡の効率性
均衡な取引
完全競争市場では、需要曲線と供給曲線の交点で価格と取引量が決まる
$${P^{*}}$$・・・均衡価格
$${Q^{*}}$$・・・均衡取引量
※均衡:需要量と供給量の釣り合っている状態

価格が$${P^{'}}$$のとき
供給量 > 需要量 ⇒ 価格が下がる
価格が$${P^{''}}$$のとき
供給量 < 需要量 ⇒ 価格が上がる
以下では、完全競争市場(の均衡取引)において資源配分が最効率化されるということを説明する
資源配分が効率的であるための条件
①市場で決まる取引量が社会的にみて最適
⇒均衡取引量において総余剰(消費者余剰+生産者余剰)が最大化される
②均衡取引量を生産する費用が最小
⇒市場均衡によって決まる各企業の生産量における費用の合計が最小
③消費者の満足度の合計が最大である
⇒市場均衡で決まる各消費者の満足度の合計が他のいかなる場合よりも大きい
これらの条件の正当性について示していく
①市場で決まる取引量が社会的にみて最適
これを示すためには、均衡取引量での取引で総余剰が最大になることを確かめればよい。
a.均衡取引量における総余剰 > 均衡取引量より少ない場合の総余剰
b.均衡取引量における総余剰 > 均衡取引量より少ない場合の総余剰
これらが示せれば、均衡取引量で総余剰は最大になる
a.均衡取引量における総余剰 > 均衡取引量より少ない場合の総余剰のとき


取引量を$${Q}$$に制限し、価格を$${P}$$とする場合

価格を変えても総余剰の最大の大きさは同じ
$${Q^{*}}$$よりも少ない取引量の場合には必ず▷のデッドスペースが生じる
⇒
市場均衡で決まる取引量における総余剰
> 市場均衡より少ない取引量における総余剰・・・(1)
b.均衡取引量よりも多い場合

企業に$${Q}$$まで生産・供給させる。また価格は$${P}$$に設定する

価格に関わらず総余剰の大きさは▷-◃
均衡取引量より多い時必ず-の部分が生じる
⇒
均衡取引量における総余剰
> 均衡取引量より多いときの総余剰・・・(2)
(1),(2)より均衡取引量において総余剰は最大化される
②均衡取引量を生産する費用が最小
これを示すためには、市場均衡によって決まる各企業の生産量における費用の合計が最小であることを確かめればよい。
つまり、均衡取引量でないいかなる場合の費用よりも均衡取引量のときの費用が最小となることを確認すればよいので、以下のパターンを考える。(正確にはbのみで良い)
a.2社の生産量を変更する場合
b.一般的な場合
a.2社の生産量を変更する場合
・市場均衡で決まる各企業の生産量の組み合わせ
($${Q^{*}_i:=$$市場均衡で決まる$${i}$$番目の企業の生産量
($${Q^{*}_1,Q^{*}_2,\cdots,Q^{*}_N}$$) ※企業数はN
($${Q^{*}=Q^{*}_1+Q^{*}_2+\cdots+Q^{*}_N}$$
・市場均衡とは異なる各企業の生産量の組み合わせ
ここで市場均衡の場合の1番目と2番目の企業の生産量を変更してみます。
($${Q_i:=$$$${i}$$番目の企業の市場均衡とは異なる生産量
($${Q_1,Q_2,Q^{*}_3\cdots,Q^{*}_N}$$) ※企業数はN
($${Q^{*}=Q_1+Q_2+Q^{*}_3\cdots+Q^{*}_N}$$
さらにここで注意すべきなのは、生産量の合計を変えないことである。つまり
$${Q_1+Q_2=Q^{*}_1+Q^{*}_2{\Rightarrow}Q_1-Q^{*}_1=Q^{*}_2-Q_2}$$
が成立することである
※総生産量を変更することを許すと、「10倍多く作った方が費用が高い」などの当たり前の現象が起こるため
ここで、変更を加えたのは1,2番目の企業のみであるので、この2つの企業の費用の合計を調べれば変更前後のどちらの費用が小さいかが分かる。



※結局四角形の面積の比較となるが、横が等しくなるため、縦の大きな費用の増加側の方が面積が大きくなる
b.一般的な場合
・生産量を減らした企業の場合


上のグラフより
生産量を減らした企業の費用の減少の合計
< $${P^{*}\times}$$減らした生産量の合計・・・(3)
・生産量を増やした企業の場合


よって
生産量を増やした企業の費用の増加の合計
> $${P^{*}\times}$$増やした生産量の合計・・・(4)
合計の生産量は$${Q^{*}}$$でなければならない(初期条件)
⇒減らした生産量の合計=増やした生産量の合計
以上から
生産量を減らした企業の費用の減少の合計
< 生産量を増やした企業の費用の増加の合計
となる。よって
市場均衡で決まる各企業の生産量における費用の合計はそれとは異なる各記号の生産量における費用の合計より小さい
つまり、
市場均衡では$${Q^{*}}$$の供給量を最小の費用で生産していることが示された
③消費者の満足度の合計が最大である
これを示すためには、市場均衡で決まる各消費者の満足度の合計が他のいかなる場合よりも大きいことを示せばよい。
そのために以下の場合を確認する。
a.2人の消費者の需要量を変更する場合
b.一般的な場合
a.2人の消費者の需要量を変更する場合
・市場均衡で決まる各消費者(n人)の需要量の組み合わせ
$${q^{*}_i:=}$$市場均衡で決まる$${i}$$番目の消費者の需要量
$${q^{*}_1,q^{*}_2,\cdots,q^{*}_n}$$
$${Q^{*}=q^{*}_1+q^{*}_2+\cdots+q^{*}_n}$$
・市場均衡とは異なる各消費者(n人)の需要量の組み合わせ
1番目と2番目の消費者の需要量を変更する
$${q_i:=}$$$${i}$$番目の消費者の市場均衡とは異なる需要量
$${q_1,q_2,q^{*}_3\cdots,q^{*}_n}$$
$${Q^{*}=q_1+q_2+q^{*}_3+\cdots+q^{*}_n}$$
また
$${q_1+q_2=q^{*}_1+q^{*}_2}{\Rightarrow}q_2-q^{*}_2=q^{*}-q_1}$$
3番目以降は変更が無いため、1,2番目の合計のみを比べればよい


以上より下の2つの条件を得る
・需要量を減らしたときの消費者の満足度の減少
> $${P^{*}(q^{*}_1-q_1)}$$
・需要量を増やしたときの消費者の満足度の増加
< $${P^{*}(q_2-q^{*}_2)}$$
また
$${q_2-q^{*}_2=q^{*}-q_1}$$
なので、2つを合わせて
需要量を減らしたときの消費者の満足度の減少
> 需要量を増やしたときの消費者の満足度の増加
よって
(2人を変更する場合)市場均衡のときの消費者の満足度の合計は、それ以外のときの消費者の満足よりも大きい
b.一般的な場合

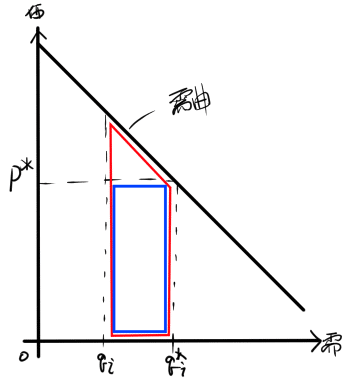


よって青い四角の面積は同じなので
需要量を減らしたときの消費者全体の満足度の減少の合計
> 需要量を増やしたときの消費者全体の満足度の増加の合計
以上より
市場均衡で決まる各消費者の需要量における満足度の合計が他のいかなる場合よりも大きくなることが確認できた。
①②③より、
資源配分は、完全競争市場において最効率化される
この記事が気に入ったらサポートをしてみませんか?
