
簡単!モータ負荷トルク計算②
加速トルク(直動系)の計算
【簡単!モータ負荷トルク計算①】の記事では、負荷トルクは、加速トルクと外的負荷トルクの和、負荷トルク=①加速トルク+②外的負荷トルク
で求められ、この内、①加速トルクは大きく分けて、回転系の運動によって生じる加速トルクと、直動系の運動に生じる加速トルクの2種類に分けられ、回転系の加速トルクについての計算の仕方を紹介しました。また、一連の負荷トルクを導くための計算の流れを紹介しました。今回は、直動系の運動よって生じる加速トルクの計算の仕方を紹介します。
※【簡単!モータ負荷トルク計算①】の記事に目を通してから、本記事を読んだ方が、より理解を深めることが出来ると思います。
【簡単!モータ負荷トルク計算①】で紹介したように、①加速トルクは以下の式で求められます。
①加速トルク:Tr=Ixω’ (g・cm)
Iとは?I=J/g になります。(g(重力加速度)=980(cm/s^2))
ω’とは?角加速度〔rad/s^2〕になります。
Jとは?以下になります。
直動系のイナーシャ計算式にあるJ
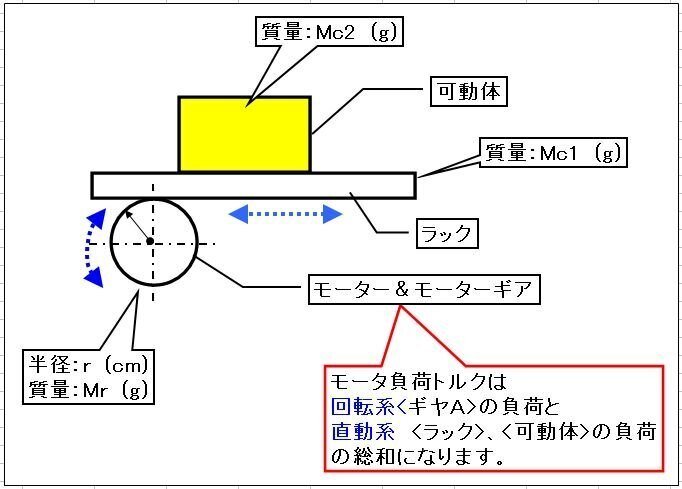
直動によって発生する直動系イナーシャ(Ic)は、【図-1】のように、直動する物体(以下ワークと記載)の質量(=M(g))と単位移動量(=A(cm/rev))の2点の要素によって決まり、式は以下になります。
J = M x (A/2π)^2 (g・cm2) (^2=2乗の意味)
但し、Mは直動するワーク質量の総和(M=Mc1+Mc2)で、単位は(g)、Aはモータ1回転当たりのワークの移動量(cm)で、単位は(cm/rev)となります。
同じJでも回転系のJの式とは異なります。ですが、直動系のイナーシャIcは下記のようになり、回転系のイナーシャIrと同じになります。
※回転系のJの計算式は【簡単!モータ負荷トルク計算①】に掲載。
I = J/g = GD^2/4g (gf・cm・s^2)
但し、gは重力加速度 g=980(cm/s^2)
回転系と直動系で異なる点(式)は、Jとなります。
回転系のイナーシャは、ワークの質量と回転半径に影響され、直動系のイナーシャは、ワークの質量とモータ1回転当たりのワークの移動量が影響されるということが分かります。直動系イナーシャを計算する際、ここまで説明したように直動系のイナーシャの計算の他に、実際は上図のように、ギヤを用いて回転運動を直動運動に変換している場合が多いため、更に回転系のイナーシャの計算も必要になってきます。
この場合のイナーシャは最終的に、直動系イナーシャIcと回転系イナーシャIrの総和になります。
ここまでの記事、【簡単!モータ負荷トルク計算①と②】にて、モータ負荷トルク計算の導き方を紹介してきましたが、次回は、実際の計算例を紹介していきたいと思います。
その前にステッピングモータの概要、駆動制御に必要な基礎知識をご紹介しておきます。角加速度の分かりやすい求め方は、【簡単!モータ負荷トルク計算①】に記載しておりますので、よかったらそちらの記事も参照下さい。
ステッピングモータの概要
ステッピングモーターとはパルスモーターとも呼ばれ、パルス信号を与えることによって決められたステップ単位で回転するモーターのことを言います。
【ステッピングモーターの特徴】
①位置決めがお手のもの
高精度の位置決めが簡単にできることが最大の特徴です。
②位置決めのセンサいらず
ワークの移動量に等しいパルス数を指定することにより位置決めが可能です。ステッピングモーターは1パルスあたりの動作角度が決まっているので移動量は次式で求められます。
移動量〔°度〕=ステップ角〔°度〕 x パルス数
③速度もデジタル制御
ステッピングモーターの運転速度はパルス信号の速度に比例します。パルス信号が速ければ速く、遅ければ遅くなります。パルス信号の速度〔Hz〕とステッピングモーターの運転速度〔r/min〕は、次のようになります。
モーター速度〔r/min〕=(ステップ角〔度〕/360°)xパルス速度 〔Hz〕x60〔s〕
※補足:〔r/min〕=〔rpm〕
(計算例)
ステップ角0.72°、パルス速度500Hzのモーター速度は?
モーター速度〔r/min〕=(0.72/360)x500x60=60〔r/min〕
④自己保持力がある
パルス信号がない停止している状態でも自己保持力があり位置を保つことが出来ます。
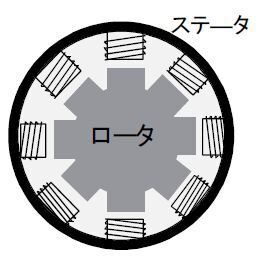
【原理】
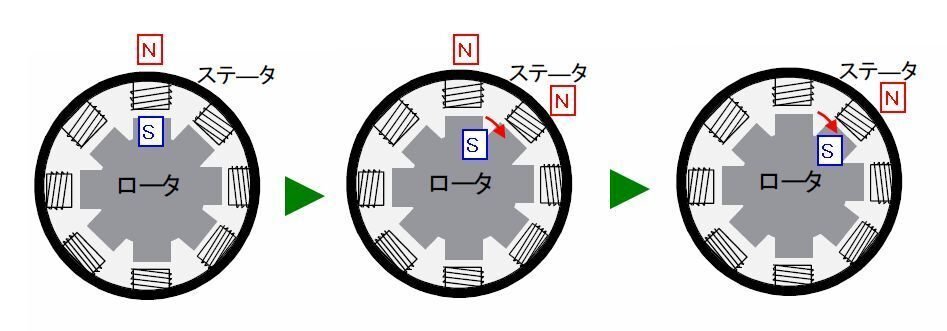
ステータ(固定子)のコイルに電流を流して磁力を発生させてロータ(回転体)をひきつけて回転させます。【図-2】
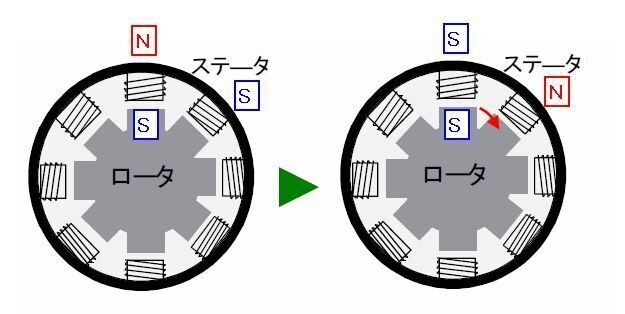
【1相励磁】で動かす
1相励磁は最も単純な方式ですが,トルクが弱く高速回転には向いていません。また,安定性が良くないため実用的ではありません。【図-3】
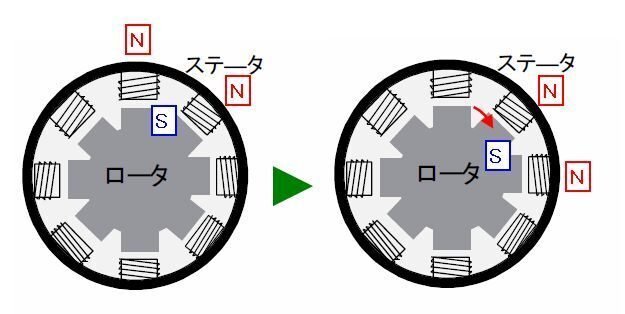
【2相励磁】で動かす
次の相と1パルス分ずつ、ずらしながら同時に励磁します。パルス幅が1相励磁の2倍となります。従って、1相励磁に比べて回転が安定して大きなトルクが得られます。但し、消費電力も2倍となります。(この方式が一般的と言えます。)【図-4】
【1-2相励磁】で動かす
1相励磁と2相励磁を交互に繰り返します。1パルスごとに回転する角度が1相励磁と2相 励磁に比べて半分になるため更に細かいモータ制御が可能になりますが、2相励磁と比較した場合、トルクは弱くなります。 【図-5】
以上がステッピングモーターの概要(原理)になります。
では、どのように制御するのでしょうか?以下に駆動制御に必要な基礎知識を紹介します。
駆動制御に必要な基礎知識
ここでは、モーターで駆動制御を行う際(またはモーターを選定する際)
なぜイナーシャの計算が必要なのか?の概要もあわせて説明します。また、ステッピングモーターを制御する上で必要なパルス数、時間、速さなどを計算例にて説明します。
【イナーシャ計算の必要性】
モーターで駆動制御を行う際(またはモーターを選定する際)、なぜイナーシャの計算が必要ななのか?
イナーシャ(慣性モーメント)は、起動時や減速時に発生する加速(減速)トルクに影響を及ぼし、イナーシャが大きくなると、それに比例して加速(減速)トルクも大きくなります。駆動制御を行う際(またはモーターを選定する際)、以下の注意が必要になります。
【ACモーターの場合】
ACモーターの場合、モーターのギヤヘッドの許容イナーシャ(許容慣性モーメント)が、負荷イナーシャ(負荷慣性モーメント)を上回る必要があります。負荷イナーシャの方が大きい場合、モーターのギヤヘッド破損につながるためです。
【ステッピングモーターの場合】
ステッピングモーターは、モーターのローターイナーシャ(ローター慣性モーメント)に対する負荷イナーシャ(負荷慣性モーメント)の比を、
「イナーシャ比=負荷イナーシャ÷ローターイナーシャ」で求め、イナーシャ比が10倍以下になるようにします。
ステッピングモーターの場合、加減速トルクに余裕があっても、イナーシャ比が大き過ぎると、加速指令についていけず脱調する場合があるためです。
【サーボモーターの場合】
モーターの許容イナーシャ(許容慣性モーメント)が負荷イナーシャ(負荷慣性モーメント)を上回るようにします。許容イナーシャより負荷イナーシャが大きいと、うまく制御できず動作が不安定となります。
【計算例】
次に、ステッピングモーターを制御する上で必要なパルス数、時間、速さなどを計算例にて説明します。
【第1問:必要なパルス数は何pls?】
基本ステップ角度2.5°のステッピングモーターがあります。1回転(360°)するためには何パルス発信する必要があるでしょう?
基本ステップ角度とは1パルスあたりのステップ角度なので、1パルスあたり2.5°回転することになります。よって、
360〔°〕/2.5〔°〕=144〔パルス〕
答え)144〔pls〕
【補足】基本ステップ角度2.5°x144〔パルス〕=360〔°〕
【第2問:回転する所要時間は何s?】
基本ステップ角度1.25°で周波数250ppsの時、90°回転する所要時間は?
まず90°回転するためのパルス数を求めます。
90〔°〕/1.25〔°〕=72〔パルス〕(=72〔pls〕)
【補足】基本ステップ角度1.25°x72〔パルス〕=90〔°〕
ここで、ppsとは1〔s〕間に発信するパルス数のことを言います。つまり250ppsとは1〔s〕間に250パルス発信すると言う意味です。よって、
72〔pls〕/250〔pps〕=0.288〔s〕
答え)0.288〔s〕
【第3問:回転する速度は何r/min?】
上記②の条件で周波数500ppsの時のモーター速度〔r/min〕は?
モーター速度〔r/min〕(=rpm)は1分間に何回転するのか?と言うことです。まず、1パルスあたり何回転するのか求めます。基本ステップ角度は1.25°ですので、
1.25〔°〕/360〔°〕=0.00347〔回転〕
1パルスあたり0.00347回転することがわかったので次に1分間に何パルス発信するのか求めます。
500〔パルス〕x60(s)=30000〔パルス〕
よって、
0.00347〔回転〕x30000〔パルス〕=104.17〔r/min〕(=rpm)
となります。
答え)104.17〔r/min〕(=rpm)
以上になります。
次回は、モータ負荷トルクの回転系、直動系の実際の計算例についてご紹介をしていきます。
よろしければサポートお願いします。 いただいたサポートは技術者としての活動費に使わせていただきます。
