
簡単!モータ負荷トルク計算①
負荷トルクの計算式
負荷トルクは、加速トルクと外的負荷トルクの和、で求められます。
負荷トルク=①加速トルク+②外的負荷トルク
補足:単位系は,(g・cm)←この単位は意外と重要(gf・cm)とは違うので注意が必要です。
負荷トルクとは、モータで物体(=ワーク:以下ワークと記載)を動かす際に必要なトルクを意味します。負荷トルクがモータのトルクを上回ると、モータでうまく動かすことが出来ない(制御できない)、と言うことになります。そのため、負荷トルクを事前に計算することは、即ち適切なモータ選定をすること、と言うことにもなります。尚、ここでの負荷トルクとは、モータにかかる最大負荷トルク(以下負荷トルクと記載)を表します。
①
加速トルクとは、ワークが加速または減速する時に生じる負荷で、一定速度の状態では、発生しない負荷となります。加速トルクを計算する際には、最も負荷がかかる加速時(または、減速時)での計算をします。
②
外的負荷トルクとは、ワークに常にかかる力、摺動抵抗やバネ力など、のことを表しています。
では、はじめに加速トルクについて説明していきます。まず、加速トルクには大きく分けて、回転系の運動によって生じる加速トルクと、直動系の運動に生じる加速トルクの2種類に分けられます。
いずれの場合も、加速トルク(=Tr:以下加速トルクをTrと記載)は、慣性モーメント(=イナーシャ:以下イナーシャをIと記載)と角加速度(=以下ω’と記載)の積で求められます。
①加速トルク:Tr=Ixω’ (g・cm)
イナーシャIの計算式は、回転系イナーシャ(以下Irと記載)、直動系イナーシャ(以下Icと記載)の場合でそれぞれ計算式が異なります。(便宜上、回転系をIr、直動系をIcと表記していますが、どちらもイナーシャIと同じ意味です)
流れはこのようになります。
①加速トルク:Tr=Ixω’ (g・cm)
なので、以下を求めます。
Iとは?I=J/g になります。(gは重力加速度)
Jとは?J=MxK^2 になります。(Mは物体の質量)
Kとは?回転半径や回転軸、重心、形状によって公式によって導きます。
ω’とは?角加速度 です。計算の仕方を分かりやすく説明します。
以下、詳細を説明しますが、直動系イナーシャには、回転系のイナーシャも含まれるため、まずは、回転系のイナーシャを理解した上で、直動系のイナーシャに進むことをおすすめします。
当サイトで公開中の全ての情報はファイル構成やデータを改変しない限り、転載や配布は基本的に自由です。各情報の利用に際しては熟読の上、自己責任でお願いします。
【ご注意】
当サイトに情報・資料を掲載する際には細心の注意を払っておりますが、誤り等が含まれる可能性があります。万一、当サイトに掲載されている情報及び内容に含まれる誤りによって被害・損害等が発生したとしても、管理(投稿)者は一切責任を負うものではありませんのでご了承下さい。
回転系イナーシャ(I)の計算式
はじめに、(水平)回転の運動によって生じるイナーシャIr(=慣性モーメント)について説明します。
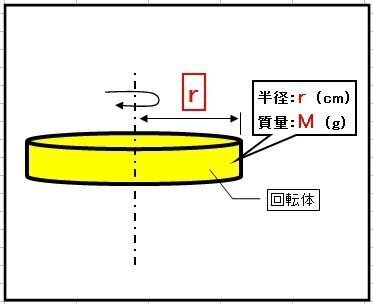
回転の運動によって発生する回転系イナーシャIrは、下記の図のように、回転運動をする物体(以下ワークと記載)の質量(=M(g))と半径(=r(cm))の2点の要素によって決まり、式は、
J = M x K^2 (g・cm2) 但し、K2 = r^2/2
(Kの2乗) (rの2乗/2)
となります。(あれ?Jって何?)
Jとは、イナーシャI(アイ)と同様にイナーシャの計算式で良く用いられる表記で、同じイナーシャJ、という意味です。
どういうこと?かというと、単位系が異なる表記の違い、であり、主にイナーシャの計算では、このJをよく使用するこになります。
もう少し詳しく説明すると、イナーシャには、主に下述のような3つの表記があり、それぞれの関係式が存在します。どれも同じ意味なのですが単位系が異なると数値が異なるので注意が必要です。簡単に言うと1(kgf)と9.8(N)は同じ意味ですが、単位系が異なると数値が異なります。イナーシャも同様です。尚、一般的に多く使用されているイナーシャの表記は、下記の①Jが多いです。
イナーシャの表記の違いに注意しましょう。
① J (ジェイ) (g・cm^2)
② GD2 (ジーディースケア) (gf・cm^2)
③ I (アイ) (gf・cm・s^2)
また、それぞれの関係式は、下記のようになります。
① J = GD^2/4 (g・cm^2)
② GD^2 = 4J (gf・cm^2)
③ I = J/g = (GD^2/4)/g (gf・cm・s^2)
※補足:gは重力加速度 g=980(cm/s^2) ^2=2乗
【まとめ】
回転系イナーシャの計算式
J = M x K^2 (g・cm2) 但し、K^2 = r^2/2
Ir = J/g = (GD^2/4)/g (gf・cm・s^2)
但し、gは重力加速度 g=980(cm/s^2)
※補足:Mは回転体の質量(g)
K^2(=Kの2乗)は、r^2/2(=rの2乗/2)
rは、回転体の半径(cm)
Irは、Iです。
直動系イナーシャIcと区別するため便宜上Irと表記しています。
即ち、(水平)回転の運動によって生じるイナーシャは回転体の質量(M)と回転体の半径(r)の2乗の半分との積となります。
ここまで説明したイナーシャの計算式は、図のように重心が回転の中心軸に位置しています。また、形状が円形になっています。重心が回転の中心軸からズレている場合や、形状が長方形や正方形などの場合は、上述にて説明をしたK^2の式が異なりますので、注意が必要です。
異なるK^2の代表例は、次に紹介しておきます。
イナーシャJ=MxK^2の K^2の代表例(式)
【回転軸が物体の重心と同じ場合のK^2(=Kの2乗)】

【図-1】円柱形状のK^2
K^2=r^2/2(補足:rの2乗÷2)

【図-2】中抜き円柱形状のK^2
K^2=(r1^2+r2^2)/2(補足:(r1の2乗+r2の2乗)÷2)

【図-3】四角柱形状のK^2
K^2=(a^2+b^2)/3(補足:(aの2乗+bの2乗)÷3)
【回転軸が物体の重心と異なる場合のK^2(=Kの2乗)】
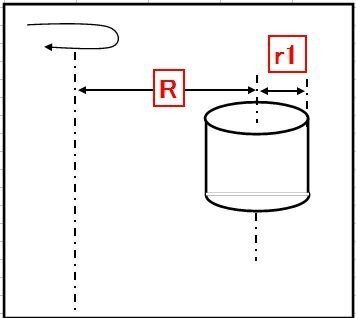
【図-4】回転軸から離れた円柱形状のK^2
K^2=(r1^2/2)+R^2(補足:(r1の2乗÷2)+Rの2乗)

【図-5】回転軸から離れた中抜き円柱形状のK^2
K^2=((r1^2+r2^2)/2)+R^2(補足:((r1の2乗+r2の2乗)÷2)+Rの2乗)

【図-6】回転軸から離れた四角柱形状のK^2
K^2=((a^2+b^2)/3)+R^2(補足:((aの2乗+bの2乗)÷3)+Rの2乗)
【回転軸が重心X0から外れるX1軸の場合のK^2(=Kの2乗)】

【図-6】回転軸が重心から外れた四角柱形状のK^2
K^2=(a^2+b^2+12xL^2)/12(補足:(aの2乗+bの2乗+12xLの2乗)÷12)但し、LはX0軸とX1軸の距離(cm)カムのような楕円形状においても、疑似的にこの式で対応可能
【回転する形状が複雑な形状の場合のK^2(=Kの2乗)】


複雑な回転する形状(=ワーク形状)は、上記に記載した「単純(基本)な形状に分解して」それぞれのイナーシャを求めていきます。最後は「求めたそれぞれイナーシャの和」になります。分解前(図-8)と分解後(図-9)の形状は上記のようになります。単純な形状に分解することで計算が容易にできるようになります。
以上のことより、K^2(Kの2乗)が求められるようになります。
つまり、
加速トルク:Tr=Ixω’ (g・cm)
のIを算出できるようになります。
I=(Ir =) J/g = (GD^2/4)/g (gf・cm・s^2)
但し、gは重力加速度 g=980(cm/s^2)
J = M x K^2 (g・cm2) 但し、K^2 = r^2/2
(Mは物体の質量、K^2はそれぞれの形状で算出)
では、次にω’(角加速度)の算出をします。
角加速度ω’の求め方
改めてwikipediaで角速度を調べると、「角速度とは物体や質点の回転の速さを表す量であり、角度と時間の商で定義される。」と出てきます。まぁ、ちょっと分り難いです。
簡単に説明すると下図のように物体をモータで動かす場合、まずはスタートから加速させ、最高速度になった時点で一定とし、停止する際、減速をさせます。一般的な基本駆動波形が下図のようになりなります。
ここで、Y軸は速度、X軸が動作に要した時間、面積が移動距離になります。
つまり、角加速度(直線動作での加速度も同様)は加速(または減速)時の斜面の直線がそれに該当します。

(図-10)で記載しているようにVmaxを単位〔rpm〕にて算出しましたが、角速度ω単位(rad/s)もVmax〔rpm〕も単位系が異なるだけで、同じことなのです。(補足:rpm 1分間に回転する回転数)
もっと分りやすく言えば、駆動波形の台形面積が、下記のような意味を持つことになります。
【Y軸 Vmax〔rpm〕系の場合】
台形面積(移動量)は θ〔°〕で表されます。
【Y軸 ω〔rad/s〕系の場合】
台形面積(移動量)は θπ/180〔rad/s〕で表されます。どちらも表し方がことなるだけで同じ意味なのです。
回転角度θの求め方
上図の台形の面積が回転角度θです。
面積なので、(t1 x Vmax)/2 + (t2 x Vmax) +(t3 x Vmax)/2 =θです。
ここで、t1=t3なので、
(t1+t2) x Vmax=θ
となります。
以上のことより、
①加速トルク:Tr=Ixω’ (g・cm)
のIとω’が求めれました。
では、実際に簡単な計算例題を行ってみましょう。
【例題】モーター負荷トルクを求めてみよう!


円柱物体の外周に摺動抵抗が100gかかる水平回転運動する質量:300g、回転半径:3cmの円柱物体が0.7sかけて270°回転する場合の負荷トルクを求めましょう。但し、動作は基本駆動波形(図-12)とし、モーターは回転軸に直結しているものとします。
負荷トルクの計算式
冒頭に記載したように、負荷トルクは、加速トルクと外的負荷トルクの和、で求められます。
負荷トルク=①加速トルク+②外的負荷トルク
補足:単位系は,(g・cm)←この単位は意外と重要(gf・cm)とは違うので注意が必要です。
まずは、①加速トルクを求めます。
加速トルクの式は、以下になります。
①加速トルク:Tr=Ixω’ (g・cm)
まずは、Iを求めます。
I=(Ir =) J/g = (GD^2/4)/g (gf・cm・s^2)
但し、gは重力加速度 g=980(cm/s^2)
J = M x K^2 (g・cm^2)
但し、K^2 = r^2/2(←回転軸が物体の重心と同じ円柱形状の場合)
です。
質量M:300g、回転半径r:3cm
J=(MxK^2=)Mxr^2/2 =300x(3x3)/2 =1350 (g・cm^2)
よって、
I=J/g=1350/980 ≒1.38(gf・cm・s^2)
次に、物体の角加速度を求めます。
(図-12)より ω'(角加速度)=ω/t1 〔rad/s2〕で求められます。
以下、<手順1>~<手順3>のステップ順にて求めていきます。

【手順1】
まず、駆動波形において、(図-13)のように台形面積が移動量(θ=270°)を表しています。台形の面積は、図の赤い面積部分の面積と一致するので、Y軸である速度Vmax(rpm)を求めることができます。
※補足
<手順2>の理解をしやすくするため、また、角速度を理解しやすくするため、まずは順を追って、Vmaxを〔rpm〕(=r/min)求めます。
(t1+t2)xVmax=θより、
Vmax=θ/(t1+t2)=270/(0.3+0.1)=675 〔°/s〕
Vmax=675〔°/s〕より、
=675/360=1.875〔回転/s〕となり、
=1.875x60=112.5〔rpm〕となります。
※補足(rpm:1分間の回転数)
1s間に675°回転するので、360°で割れば、1s間に1.875回転するので、60sでは、112.5回転することになります。
【手順2】
(図-13)の駆動波形で言うところのY軸が角速度(rad/s)にあたります。
<手順1>でVmaxを〔rpm〕にて算出しましたが、角速度ωもVmax〔rpm〕も単位系が異なるだけで同じことなのです。もっと分りやすく言えば、駆動波形の台形面積が、
Y軸 Vmax〔rpm〕系の場合、台形面積(移動量)は θ〔°〕で表し、
Y軸 ω〔rad/s〕系の場合、台形面積(移動量)は θπ/180〔rad/s〕で表します。どちらも単位系が異なるだけで同じ意味なのです。
因みに、角加速度とは駆動波形での台形波の最初の斜辺が角加速度となります。(要は加速度と同じ意味です。)
よって、
(t1+t2)xω=θπ/180 〔rad/s〕より、
(0.3+0.1)xω=270xπ/180 ω=3.75π〔rad/s〕
【手順3】
角加速度ω’の計算
ω'=ω/t1 〔rad/s2〕より、
ω’=3.75π/0.3=12.5π〔rad/s2〕
以下、加速トルクが求められます。
①加速トルク:Tr=Ixω’ (g・cm)
I≒1.38(gf・cm・s^2)
ω’=12.5π〔rad/s^2〕
①加速トルク:Tr=Ixω’=1.38x12.5π ≒54.17(g・cm)
となります。
ここで、おさらいです。
モータ負荷トルクの計算は、以下になります。
負荷トルク=①加速トルク+②外的負荷トルク
ですので、①の加速トルクが求められました。
次に②の外的負荷トルクの算出が必要になります。
次に、②外的負荷トルクを求めます。
外的負荷トルクとは、ワークに常にかかる力、摺動抵抗やバネ力など、のことを表しています。
ここで、半径r=3cmの円柱外周に100gの摺動抵抗がかかる想定です。
モーターにかかる負荷トルクは、(g・cm)で表します。
つまり、回転軸から1cm離れた箇所に何g負荷がかかるか?になります。
回転軸から3cm離れた箇所に100gの摺動抵抗がかかった場合、1cm離れた場所では、てこの原理(レバー比率)が働きます。
外的負荷トルクは以下で求められます。
②外的負荷トルク:Tr’=(3cm)/1(cm)) x 100(g)=300(g・cm)
よって、モータ負荷トルクは以下になります。
負荷トルク=①加速トルク+②外的負荷トルク
=54.17+300 =354.17(g・cm)となります。
モータの選定
モ-タを選定する際、安全率Sを考慮する必要があります。
安全率S=2とした場合、負荷トルク=354.17 x 2≒708(g・cm)となり、モータの最大負荷トルクが、708(g・cm)以上のモータを選定しておくことが無難と言えるでしょう。
計算しておくことのメリット
このように、計算することによって、負荷トルクに影響する要素が分かるようになることも計算を行うメリットの1つです。
今回の例題のような場合、加速による負荷よりも摺動抵抗における負荷がおよそ86%占めているため、摺動抵抗の変化における負荷トルクへ影響を注視すべきことが分かると思います。
最後に冒頭で記載した回転系のイナーシャの計算例を記載しておきます。
昨今、設計する際は3D-CADを用いて設計することが一般的ですので、CADでイナーシャIの自動計算できますが、理論値を把握しておくことは大切なことですので、以下、記載しておきます。
イナーシャJ=MxK^2の K^2の計算例
(水平)回転運動によって発生する回転系イナーシャの計算例です。ここでは下記①~③の公式にあてはめて計算してみます。(単位系が異なるだけで意味は同じです。)
【イナーシャJ,イナーシャGD^2,イナーシャI】
①J=GD^2/4 (g・cm^2)
②GD^2=4J (gf・cm^2)
③I=J/g=(GD^2/4)/g (gf・cm・s^2)
※補足:gは重力加速度 g=980cm/s^2
1.中抜き円柱形状の計算例
K^2 K^2=(r1^2+r2^2)/2(補足:^2→2乗)

(図-14)水平回転運動する質量:150g、外径:4cm、内径:2cmの回転イナーシャを求めましょう。
①J=(MxK^2=) M x (r1^2+r2^2)/2=150 x (4x4+2x2)/2 =1500 (g・cm^2)
②GD^2=4J=4 x M x (r1^2+r2^2)/2=4 x 150 x (4x4+2x2)/2=6000(gf・cm^2)
③I=J/g=(GD^2/4)/g = (150 x (4x4+2x2)/2)/980=1.53(gf・cm・s^2)
計算からも分かるように、イナーシャは回転体の質量よりも最大回転半径に大きく影響されることが分かります。理論計算を事前に計算しておくことによりイナーシャがどの要因に影響されやすいか、を見極める手がかりになります。
2.四角柱形状の計算例
K^2=(a^2+b^2)/3(補足:^2→2乗)

(図-15)水平回転運動する質量:400g、a:2cm、b:3.5cmの回転イナーシャを求めましょう。
①J=(MxK^2=) Mx(a^2+b^2)/3=400x(2x2+3.5x3.5)/3=2166.7(g・cm^2) ②GD^2=4J=4xMx(a^2+b^2)/3=4x400x(2x2+3.5x3.5)/3 =8666.8(gf・cm^2) ③I=J/g=(GD^2/4)/g =(400x(2x2+3.5x3.5)/3)/980 =2.2(gf・cm・s^2)
3.回転軸から離れた円柱形状の計算例
K^2=(r1^2/2)+R^2 (補足:^2→2乗)

(図-16)水平回転運動する質量:75g、R:4cm、r1:1.5cmの回転イナーシャを求めましょう。
①J=(MxK^2=)Mx((r1^2/2)+R^2) =75x((1.5x1.5)/2+4x4)
=1284.375(g・cm^2)
②GD^2=4J=4xMx(r1^2/2+R^2=4x75x((1.5x1.5/2)+4x4) =5137.5(gf・cm^2)
③I=J/g=(GD^2/4)/g=75x((1.5x1.5/2)+4x4)/980=1.310(gf・cm・s^2)
4.回転軸から離れた中抜き円柱形状の計算例
K^2=((r1^2+r2^2)/2)+R^2(補足:^2→2乗)

(図-17) 水平回転運動する質量:150g、R:4cm、r1:2cm、r2:1.5cmの回転イナーシャを求めましょう。
①J=(MxK^2=)Mx[((r1^2+r2^2)/2)+R^2] =150x[((2x2+1.5x1.5)/2)+4x4] =2868.75(g・cm^2)
②GD^2=4J=4xMx[((r1^2+r2^2)/2)+R^2]=4x150x[((2x2+1.5x1.5)/2)+4x4]=11475(gf・cm^2)
③I=J/g=(GD^2/4)/g=150x[((2x2+1.5x1.5)/2)+4x4] /980=2.927(gf・cm・s^2)
5.回転軸から離れた四角柱形状の 計算例

(図-18)水平回転運動する質量:400g、a:2cm、b:2.5cm、R:8cmの回転イナーシャを求めましょう。
①J=(MxK^2=) M x [((a^2+b^2)/3)+R^2] =400 x [((2x2+2.5x2.5)/3)+8x8] =26966.7(g.cm^2) ②GD^2=4J=4xMx[((a^2+b^2)/3)+R^2]=4x400x[((2x2+2.5x2.5)/3)+8x8]=107866.7(gf/cm^2)
③I=J/g=(GD^2/4)/g=400x[((2x2+2.5x2.5)/3)+8x8] /980=27.5(gf・cm・s)
次回は、直動系の負荷トルクの計算式をご紹介します。
よろしければサポートお願いします。 いただいたサポートは技術者としての活動費に使わせていただきます。
