【陰影の描き方】面を意識して描くとは何か
陰影の描き方について調べることはイラストを描いたことがある人ならどんな方でもやったことがあると思います。その時頻繁に登場するアドバイスが「面を意識して描きます」というフレーズです。
私も散々聞いてきましたが、長い間理解ができなかったためこう思ってました。
「その意識の仕方を教えてくれよ!」と。
そこで本記事では面を意識するとは何か、具体的にどうやるのかについて言葉で説明できるようにすることを目指します。
なお、本記事では理論的な要素を高めるために数学の力(高校数学の数学Ⅰ程度の知識)を借りますが、内容自体は数式なしでも理解できるよう努めます。
予備知識
今回の話題に必要な予備知識を簡単に説明します。内容がわかっている方は飛ばしていただいて構いません。
2種類の陰影
イラストにおいて、陰影という言葉は大きく分ければ2つの役割があります。その役割は以下のとおりです。
シェード:光が届かない場所にできる陰影のこと。
シャドウ:物が光を遮ることによってできる陰影のこと。
図にすれば以下のようになります。

本記事では、面を意識するとは何かについての解説となりますので、シェードについて扱います。なお、シャドウについてはまたどこかで解説できたらいいなと思ってます。
光が見える仕組み
例えばりんごは赤く見えます。その理由は様々な光の成分のうち赤い光のみが反射するためです。流れとしては以下のようになります。

光が物体に当たります。今回は太陽光を想定しています(太陽光は様々な色の成分を含んでいることに注意)。
光がりんごに当たると赤色以外の成分はすべて吸収します。
赤い光のみ反射します。
赤い光が目に入るため、りんごは赤色と認識します。
ランベルトの余弦則
本記事で最も伝えたいことがランベルトの余弦則です。この法則は面を意識して描くというアドバイスを数学的に表現したものです。
図形的な解説①:光源と面が垂直の関係の場合
いきなり数式から入ると難しいため、イメージを掴むための解説を行います。まず1つの光源と1つの面から構成される以下のような状況を考えます。

ここから光源が光を発します。以降、光は以下の図のように矢印を使って表現していきます。

光が物体に当たると、一部の光は物体が吸収し、残りの光は反射します。そして反射した光は目に入り、それが色として認識します。

図形的な解説②:光源と面が垂直ではない場合
続いて、面を傾けた場合の光の反射について解説をします。まず先ほどと同様に1つの光源と1つの面を考えます。先ほどと違うのは面が傾いているところです。

ここで光源から光を当てます。このとき、面が傾いているため先ほどよりも面に当たる光は少なくなります。

光の反射の考え方は先ほどと同じです。当たった光のうち一部の光は吸収し、残りの光は反射します。そして反射した光は目に入り、色として認識できます。

ここからわかることは面が傾くと入射する光が減るため、反射後の光も少なくなります。そして、面が地面の角度に近くなるほど入射する光が少なくなり反射する光も少なくなるため、面自体が暗くなっていきます。
以上より、光源の向きと面の向きの角度の開きが大きいところがシェードになるということが導けます。
物理学的な解説
この章は数学に抵抗がない方向けの内容となっています。なお、読み飛ばしても次の内容に影響はないようにしています。
ランベルトの余弦則とは、反射する単位面積あたりの光の強さ$${I_{\theta}}$$は物体に入射する単位面積当たりの光の強さ$${I_{0}}$$の余弦に比例するもの。式で表すと以下のようになります。
$$
I_{\theta}={I}_{0} {k}_{D}cos \theta
$$
なお、ここで$${\theta}$$は入射する光と面のなす角、$${k_{D}}$$($${0 \leqq k_{D} \leqq 1}$$)はその面の拡散反射率となります。
ここからは詳細な解説を行います。なお、イラストに応用することが主目的ですので厳密な話はしません。
先ほどと同じように1つの光源と1つの傾いた面を考えます。この時、光源の強さは単位面積当たり$${I_{0}}$$、面の傾きは$${\theta}$$とする。

入射した光は傾いている面に当たります。このとき、面に当たる光の強さの合計は同じです。しかし放射中の光より面に当たったときの光の方が当たる面積が大きいため、単位面積当たりの光の強さは弱くなります。具体的には三角比の定義より$${cos \theta}$$倍になります。よって、面に当たる単位面積当たりの光の強さは$${I_{0} cos \theta}$$となります。

最後に反射する光の量を考えます。
面の拡散反射率を$${k_{D}}$$とするとき、反射する光の単位面積あたりの強さは$${k_{D} \times I_{0} cos \theta = k_{D} I_{0} cos \theta}$$となります。

以上がランベルトの余弦則の物理学的な解説となります。
具体例①:立方体におけるシェード
ここからいよいよ本題となります。ランベルトの余弦則を使って実際のイラストへ応用していきましょう。しかし、いきなりイラストへの応用は難しいためまずは単純な面である立方体を使って考えていきましょう。
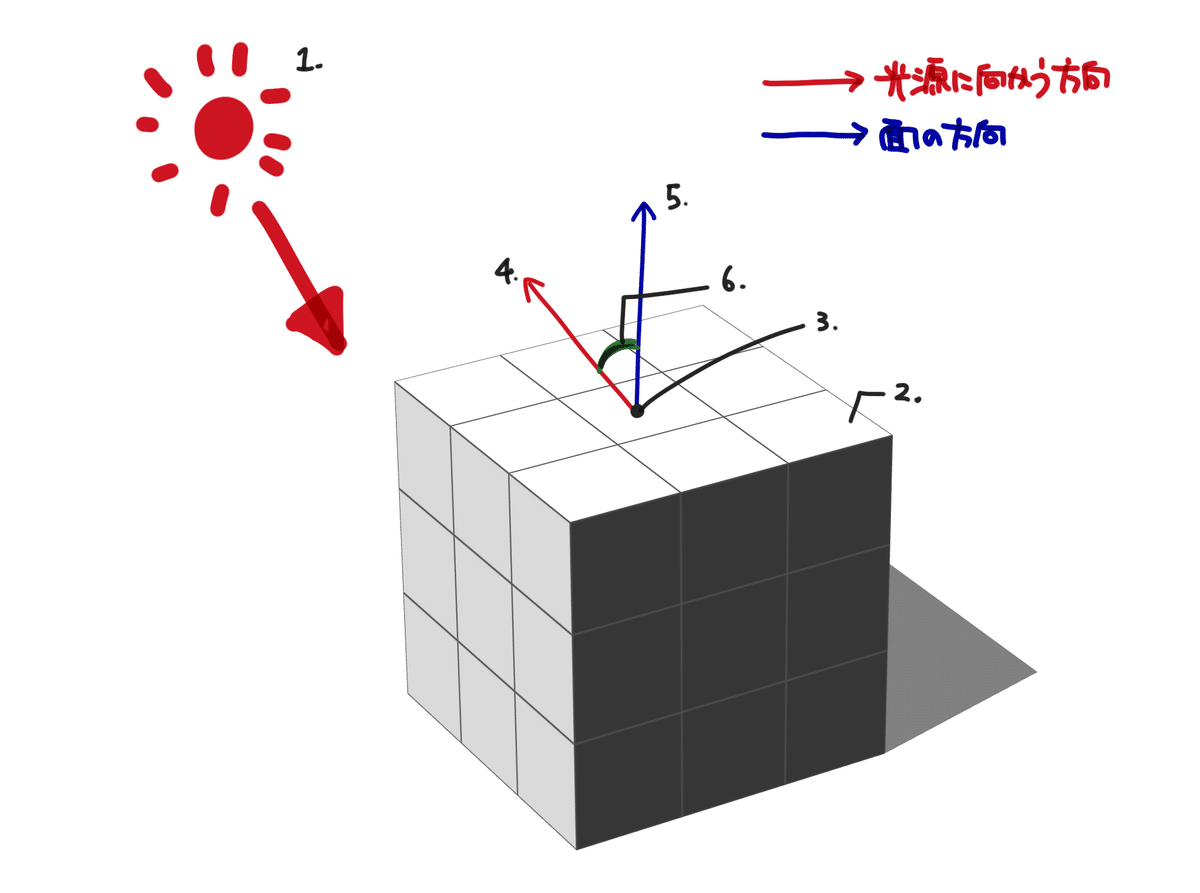
以下の図のような1つの光源と1つの立方体を考えます。なお、便宜上6つの面に①~⑥の名前を付けておきます。

ランベルトの余弦則を使った明暗の決定方法
ランベルトの余弦則を使った明暗の決定方法は以下の手順になります。
光源の向きを決める。
注目する面を決める。
注目する面の上に自由な1点を決める。
自由に決めた1点を始点にして、光源に向かう方向へ矢印を引く(向きに注意すること)。
面と垂直になり、かつ物体の外側に向かうように矢印を引く。
光源に向かう方向の矢印(赤の矢印)と面と垂直な矢印に引いた矢印(青の矢印)の角度を見る(以降、この角度のことを「光源と面法線のなす角」と呼ぶことにする)。
光源と面法線のなす角をすべての面で求め、なす角の大小関係を比較することでシェードを決定する(なす角が小さいほど明るい面)。
面の明るさを決める
先ほど示した方法を使って光源と面のなす角をそれぞれ求めると以下のようになります。なお、面⑥は地面と接しているためここでは考えません。


では、求めたなす角から面の明るさを決定していきます。
面の明るさは光源と面法線のなす角が小さいほど明るくなります。図より、なす角の大小関係は$${{\theta}_{3}<{\theta}_{4}<{\theta}_{2}<{\theta}_{5}<{\theta}_{1}}$$となるため、面の明るさは①<⑤<②<④<③となります。
以降は補足です。
光源と面法線のなす角が90°を超えると光源の裏側に面があることになります。よって、90°以上では光が一切届かない状態となります。上記の図では③、④がその状態に該当します。
具体例② 腕を塗る
ではいよいよ実際のイラストへ応用していきましょう。今回は腕の塗りを具体例にして考えていきます。
使用するイラストは下記となります。

手順1:光源の向きを決める
まず光源の向きを決めます。今回は下から光を当ててみます。
なお、向きの決め方については別途記事を描く予定ですのでここでは省略とします。

手順2:面を明示する
腕に関する面を明示します。今回は解剖学の本を見ながら面を記載しています。私の場合、面について考えるときは観察、解剖学、実際に触ってみるなどの方法を使用しています。

手順3:明示した面と光源の向きからシェードを特定する
ここまで終われば光源と面法線のなす角を考えてシェードを塗っていくだけです。考え方は先ほどの立方体の時とほぼ同じです。今回は1影、2影、ハイライトの3つを塗っています。




まとめ
本記事では、ランベルトの余弦則を使ったシェードの決め方について解説しました。重要なポイントは以下となります。
「面を意識する」とは、光源と面法線のなす角を考えて明部か暗部かを決めることである。
面を意識するためには物体の立体的な構造をあらかじめ理解しておく必要がある。
