流線、粒跡線、ラグランジュ微分 ／ 流体力学

昨日のエントリーについて、粒跡線はそれでよいのかな…というやんわりとしたご指摘を人づてに頂きました（感謝！）ので、今日は反省して、そのあたりをまじめに勉強し直して、まとめてみました。流体力学の基礎をなすコンセプト――流線、粒跡線、ラグランジュ微分といった基本的概念について。

さっそくですが、まずは、これらの直感的な意味を書きます。

★流線。テレビの天気予報で、各地の風の強さをあらわす矢印が、地図にいくつも描かれた画面がありますね。その風の強さがずっと一定のまま変わらないと想像しましょう。そして何かすごーく軽い粒子を、その一定の風に乗せて飛ばします。この粒子のえがく軌跡こそが、流線です。つまり、風のスナップショットをとって一定に保ったままにして、テスト粒子を飛ばしたときの軌跡です。

★粒跡線。時間とともに変化する（かもしれない）風に乗せて、すごく軽い粒子を飛ばしたときにえがかれる軌跡のことです。本当に風まかせの綿毛みたいなもの。おそらく、向きを変える風に乗って、あっちへ行きこっちへ行きと、すごく複雑な曲線をえがくかもしれません。もちろん、もし風がずっと一定の調子で吹き続けるならば、上の流線に一致します。

★ラグランジュ微分。まず微分とは、ざっくり、「傾き」や「変化率」のことです。そしてラグランジュ微分はとくに、何らかの量の、粒跡線に沿った微分のことです。つまり、ある瞬間のある点での風、その方向に沿って微分をする、つまり勢い込みでその向きへの量の変化率を測る感じです。

――そもそも流体力学とは、液体や気体が流れるようすを調べたり、予測しようとする分野。その流れを考えるとき、仮想的にでもテスト粒子の動きを考えることは、流れをつかむ上で便利なので、これらの概念が活躍するわけです。

それでは以下は、数式を使った説明です。
(1)流線
(2)粒跡線
(3)時空座標の偏微分
(4)ラグランジュ微分
(5)粒跡線に沿った積分と，その微分  
の順にまとめます。

(1) 流線

時空 M に，ベクトル場 v _ i ( t , x ) が与えられているときに，「流線」というものが考えられる： 
ある固定された時刻 t _ 0 における流線 c :  線分∋ s  ↦  ( t _ 0 , x ) ∈ M _{ t = t _ 0 } とは，その時刻 t _ 0 におけるベクトル場のスナップショット v _ i ( t _ 0 , x ) に対する「積分曲線」である．
（←各点における接線が，その点におけるベクトル場 v _ i ( t _ 0 , x ) と一致しているような曲線．）

いま，流線 c の座標成分を c _ i で表すなら，流線の定義方程式とその解は，それぞれ

で与えられる（じっさいに，解を s で微分してみれば定義方程式が得られる）．

(2) 粒跡線

時空 M 上に，流体場であるベクトル場 v _ i ( t , x ) が与えられたとき，そのベクトル場の時間発展までをも考慮した積分曲線 X :  線分∋ s  ↦  ( t , x ) ∈ M のことを，粒跡線とよぶ．
（仮に相対性理論の用語を借用するなら，これは要するに「テスト粒子がたどる世界線」といえよう．）

粒跡線の座標成分を X _ i で表せば，その定義方程式と解は，それぞれ

で与えられる（じっさい，解を s で微分してみれば，定義方程式が得られる）．

※通常は s と t を一致させて考えるので，次のようにも書ける： 

(3) 時空座標の偏微分

時空座標 ( t , x _ i ) 自身の，偏微分については，それぞれが独立変数であることからとくに次が成り立つ：

(4)  ラグランジュ微分

時空に流体ベクトル場 v _ i ( t , x ) が与えられているときに，任意の場の量に対してラグランジュ微分というものを考えることができる：

ラグランジュ微分は，「粒跡線に沿った微分」として定義される．ある物理的な場の量 A ( t , x ) に対して， v の粒跡線 X 上の点 X ( t ) における，粒跡線に沿った微分は，

で与えられ（※粒跡線上のパラメータ s を t と一致させて考えるのがミソ），場の量に対しては上の偏微分を使ったラグランジュ微分の表式に一致する．

※粒跡線に沿った微分は，曲線をパラメトライズする変数 s を用いて

とも書けるだろうが，頭の因子 d t / d s がいちいち登場するのを嫌って，上のように t で定義したと思われる．

★とくに，空間座標のラグランジュ微分については，空間座標がほぼ自明な x _ i ( t , x ) = x _ i という関数場だとみなせば，

のように計算される．（←神部勉ほか『流体力学』（裳華房、1995年）p.10）※ゼロにはならないことに注意．

★また，粒跡線 X ( s ) に関しては，場ではないからラグランジュ微分としては偏微分形のものを使えないはずである．しかし，もとの意味に立ちもどって，ラグランジュ微分が粒跡線に沿った微分 D / D t = d / d s | _{ s = t } で与えられるとすれば，

と定まる．
別の求めかたとしては，新しい場 X~ _ i ( t , x ) = X _ i ( t ) を定義して，これを粒跡線 X _ i と同一視すれば，形式的には偏微分形のラグランジュ微分が適用できて，

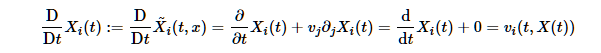
が得られる．これは本来の意味からの計算（上の結果）と一致している．

(5) 粒跡線に沿った積分と，その微分

流体力学では「粒跡線に沿った積分」という概念がよく登場する．これは「積分の経路として，ある粒跡線 X ( s ) を選ぶ」という意味である．

★たとえば，スカラー場に対しては，次のような線積分が考えられる：

★また，ベクトル場 V _ i ( t , x ) に関しては，いろいろな線積分がありうるが，

や，

といったものが例に挙げられる．後者の d X を使った表式は一般的ではないが，効率的な略記法と考えていただきたい．

逆に，これらを t 微分すると，1変数の微分の定義通りの計算により下記が得られる：

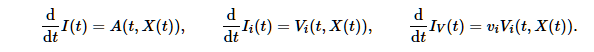
以上です。むずかしい内容でじゃっかん、エグゾースティド、かのわさびでした。ありがとうございました。

参考文献： 
神部勉編著『流体力学』（裳華房、1995年）。