
緑本第11章の空間統計モデルをRとStanで実装してみた
はじめに
このnoteでは、久保拓弥氏の著書『データ解析のための統計モデリング入門』の第11章で扱われている、空間構造のある階層ベイズモデルをRとStanで実装してみた話を書きます。
緑本の愛称でも知られるこの本は、データ分析界隈の方なら一度は聞いたことのある有名な著書だと思います。私もデータサイエンスを学んだ初期のころに知人に薦められて読みました。
とても勉強になる本なのですが1つ難点があって、MCMCでベイズ推論する際にWinBUGSというソフトウェアを使って解説されており、Macユーザーの私には実際に実行して試せない、という問題がありました。
MCMCのソフトウェアは複数あるようですが、今から学ぶならより高速に処理できると言われているStanがいいだろう、ということで馬場真哉氏の著書『RとStanではじめるベイズ統計モデリングによるデータ分析入門』で学んだ後、実際に緑本第11章をRとStanでやってみました。
緑本第11章の問題設定
詳細は実際に緑本を読んでいただくとして、ここでは簡単に紹介だけ書きます。
ある架空植物についての調査地域に、1列に並んだ50の区画があって、1〜50の番号が順番に割り振られているとします。そして各区画内に生息する架空植物の個体数を調べた結果、以下の図のようなデータが得られました。

黒丸が各区画で観測された個体数、破線はポアソン乱数で個体数データを作った時に使った場所ごとに変化する平均値です。
この架空観測データについて、ポアソン分布に従うとして統計モデリングします。ポアソン分布の平均値λの対数は、全区画に共通の大域的なパラメータβと、場所ごとに異なるパラメータrの和で表すとします。

ここで各区画とも隣接する区画とだけ相互作用する(相関がある)と仮定します。場所差rの事前分布として正規分布を設定し、この正規分布の平均μを隣接する区画のrの平均値に等しいとし、正規分布の標準偏差σはパラメータsを導入してsを隣接する区画数nの平方根で割った値とします。隣接する区画数nについては、両端の区画1・区画50はn=1、それ以外はn=2となります。

このような事前分布は条件付き自己回帰(CAR)モデルと呼ばれるそうです。
RとStanで実装する
では上記モデルをStanで記述します。
緑本にはBUGSコードが掲載されており参考にはなるのですが、少し困ったことがあります。BUGSにはCARモデルを記述するためのcar.normal関数なるものがあるのですが、私の調べた限りStanには無いようです。
なので自分で実装しないといけません。Stan初心者の私には荷が重い課題なので、とりあえずググってみました。いくつかのサイトを参照しましたが、最終的にはこちらのブログ記事を参考にしました(以後ブログ記事Aと記載)。
使っているデータは異なりますが、同じようなモデリングをされており、見たところStanのコードはほぼそのまま利用できそうです。ほとんどブログ記事Aからの転載ですが、私が実行してみたコードを記載します。
// 参照元サイト
// https://ito-hi.blog.ss-blog.jp/2014-04-20
// midori_bon_11.stanというファイル名で保存
data {
int<lower=1> N_site;
int<lower=1> N_Adj;
int<lower=0> Y[N_site];
int<lower=1> Adj[N_Adj];
real<lower=0> Weight[N_Adj];
int<lower=1> Offset[N_site, 2];
}
parameters {
real r0[N_site-1];
real beta;
real<lower=0> sigma;
}
transformed parameters {
real r[N_site];
real s[N_site];
real mu[N_site];
// ↓この部分が何をしているのか理解し切れていない
for (j in 1:(N_site-1))
r[j] = r0[j];
r[N_site] = -sum(r0);
// ↑この部分が何をしているのか理解し切れていない
for (j in 1:N_site) {
real sum_x;
real sum_w;
sum_x = 0.0;
sum_w = 0.0;
for (i in Offset[j, 1]:Offset[j, 2]) {
sum_x = sum_x + Weight[i] * r[Adj[i]];
sum_w = sum_w + Weight[i];
}
mu[j] = sum_x / sum_w;
s[j] = sigma / sqrt(sum_w);
}
}
model {
for (j in 1:N_site) {
Y[j] ~ poisson_log(beta + r[j]);
r[j] ~ normal(mu[j], s[j]);
}
beta ~ normal(0, 1.0e+2);
sigma ~ uniform(0, 1.0e+4);
}
generated quantities {
real<lower=0> Y_mean[N_site];
for (j in 1:N_site)
Y_mean[j] = exp(beta + r[j]);
}ここで、コード内の「この部分が何をしているのか理解し切れていない」と書いている部分がよく分かりません。無情報事前分布からサンプリングされる各区画のrの値の、その合計が0になるように調整している、ということだと思いますが、なぜそうする必要があるのか腹落ちし切れません。
ポアソン分布のパラメータを全区画共通のβと、区画ごとに固有のrの和で表すのだから、区画ごとに固有のrの合計は0にするべき、と何となくは理解できるような気がしないでもない…。ただ「そのほうがキレイではあるけど必須なのかな?」という疑問が自分の中には残ってます。
とりあえずStanコードは上記を利用させていただくとして、Rコードは以下のように記述しました。
# 緑本第11章で使うデータの読み込み
# データは緑本のサポートサイトで入手できます
# https://kuboweb.github.io/-kubo/ce/IwanamiBook.html
load("spatial/Y.RData")
# 前処理
initvalue <- c(0,2)
adj <- initvalue
for (i in 1:49) {
adj <- c(adj, initvalue + i)
}
adj <- adj[-c(1,length(adj))]
adj_num <- c(1, rep(2, 48), 1)
N_site = length(Y)
offset2 <- offset1 <- rep(NA, N_site)
offset1[1] <- 1
for (i in 2:N_site) {
offset1[i] <- 1 + sum(adj_num[1:(i - 1)])
}
for (i in 1:(N_site - 1)) {
offset2[i] <- offset1[i + 1] - 1
}
offset2[N_site] <- length(adj)
Offset <- cbind(offset1, offset2)
colnames(Offset) <- NULL
weight <- rep(1, length(adj))
data_list <- list(
N_site = length(Y),
N_Adj = length(adj),
Adj = adj,
Weight = weight,
Offset = Offset,
Y = Y
)
# stan実行
stan_full <- stan(
file = "midori_bon_11.stan",
data = data_list,
iter = 5000,
warmup = 2000,
thin = 1,
seed = 1
)ここで、adj・adj_num・Offsetなどの変数が各区画に隣接する区画の番号や、隣接する区画の数の情報を与えています。また変数weightを使って隣接する区画の影響の大きさを重み付けできますが、ここではすべて1にしています。
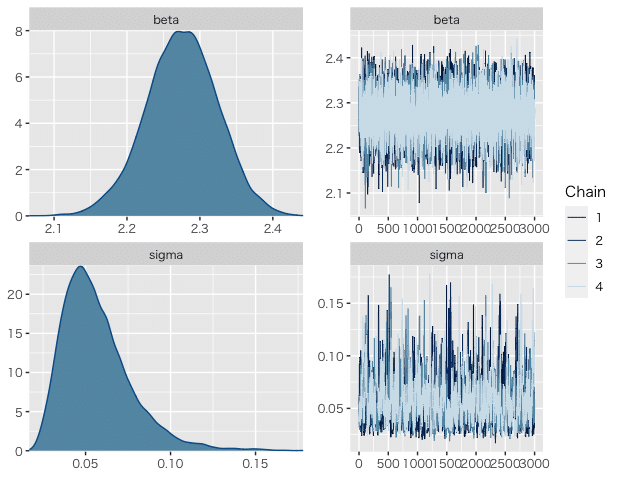
StanでMCMCを実行して得られた結果は以下のようになりました。パラメータβ(以下のbeta)に関しては緑本とほぼ同等の値が求まりました。
パラメータs(以下のsigma)については緑本の値よりもオーダー1つ小さい値が求まりました。ブログ記事Aでも、BUGSに比べてStanでやった方が分散が小さく求まったと記載されていますので、ソフトウェアにより違いがあるのかもしれません(し、別の原因があるのかもしれません)。
(出力)
mean se_mean sd 2.5% 50% 97.5% n_eff Rhat
beta 2.28 0.00 0.05 2.17 2.28 2.37 6455 1.00
sigma 0.06 0.00 0.02 0.03 0.05 0.11 677 1.01ちなみに、Stanを実行すると私の環境では以下のような警告メッセージが出ました。adapt_deltaなどパラメータ調整してみましたが、警告メッセージを無くすことまではできませんでした。このあたりのチューニング方法は今後学んでいきたい部分です。
警告メッセージ:
1: There were 34 divergent transitions after warmup. Increasing adapt_delta above 0.8 may help. See
http://mc-stan.org/misc/warnings.html#divergent-transitions-after-warmup
2: There were 1 chains where the estimated Bayesian Fraction of Missing Information was low. See
http://mc-stan.org/misc/warnings.html#bfmi-low
3: Examine the pairs() plot to diagnose sampling problems
MCMCの結果から、トレースプロットと事後分布を描画しました。トレースプロットと上記Rhatの値と合わせて、収束は問題ない(?)と言えそうです。
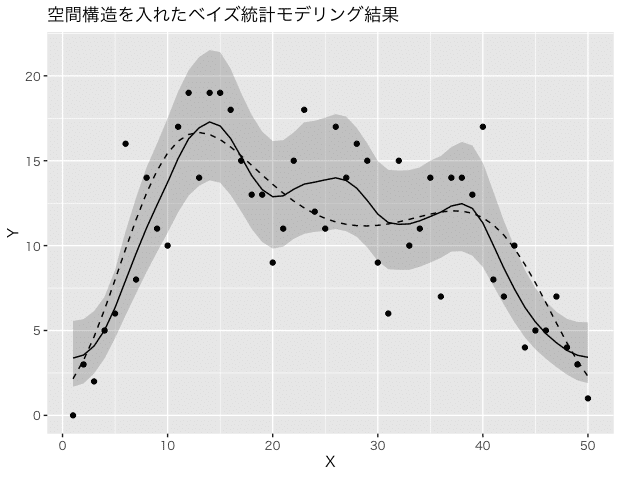
ベイズ推論結果も図示しました。黒の曲線が事後中央値、灰色のシェードがベイズ予測区間です。推定されたパラメータsが小さかったように、予測区間も緑本の図に比べて狭く見えますが、推論自体は上手くできた(?)ように見えます。
失敗例
実はブログ記事Aにたどり着く前に、自分でもStanコードを書いてトライしていました。当初はこんな感じに実装していました。まずStanコードから。
// not_good_midori_bon_11.stanというファイル名で保存
data {
int<lower=1> N;
int<lower=0> Y[N];
}
parameters {
real r[N];
real beta;
real<lower=0> sigma;
}
transformed parameters {
real mu[N];
real std[N];
mu[1] = r[2];
std[1] = sigma;
for (i in 2:(N-1)) {
mu[i] = (r[i-1] + r[i+1]) / 2;
std[i] = sigma / sqrt(2);
}
mu[N] = r[N-1];
std[N] = sigma;
}
model {
beta ~ normal(0, 1.0e+2);
sigma ~ uniform(0, 1.0e+4);
for (j in 1:N) {
r[j] ~ normal(mu[j], std[j]);
Y[j] ~ poisson_log(beta + r[j]);
}
}
generated quantities {
real<lower=0> Y_mean[N];
for (j in 1:N)
Y_mean[j] = exp(beta + r[j]);
}ブログ記事AのStanコードと違って、緑本第11章の問題設定に特化した書き方ですが、当初はこれで良いのではないかと考えていました。
次にRコードです。
# データはすでに読み込んでいる状態から開始
data_list <- list(
N = length(Y),
Y = Y
)
stan_full <- stan(
file = "not_good_midori_bon_11.stan",
data = data_list,
iter = 5000,
warmup = 2000,
thin = 1,
seed = 1
)これでStanを実行すると、全然ダメ、収束しませんでした。得られたパラメータは以下の通りです。
(出力)
mean se_mean sd 2.5% 50% 97.5% n_eff Rhat
beta -0.22 26.94 40.37 -63.53 -8.60 91.61 2 4.12
sigma 0.06 0.00 0.02 0.03 0.05 0.11 223 1.02警告メッセージもたくさん出ました。
警告メッセージ:
1: There were 1759 transitions after warmup that exceeded the maximum treedepth. Increase max_treedepth above 10. See
http://mc-stan.org/misc/warnings.html#maximum-treedepth-exceeded
2: There were 1 chains where the estimated Bayesian Fraction of Missing Information was low. See
http://mc-stan.org/misc/warnings.html#bfmi-low
3: Examine the pairs() plot to diagnose sampling problems
4: The largest R-hat is 2.64, indicating chains have not mixed. Running the chains for more iterations may help. See
http://mc-stan.org/misc/warnings.html#r-hat
5: Bulk Effective Samples Size (ESS) is too low, indicating posterior means and medians may be unreliable. Running the chains for more iterations may help. See
http://mc-stan.org/misc/warnings.html#bulk-ess
6: Tail Effective Samples Size (ESS) is too low, indicating posterior variances and tail quantiles may be unreliable. Running the chains for more iterations may help. See
http://mc-stan.org/misc/warnings.html#tail-ess
トレースプロットと事後分布も描画しました。パラメータβが全然ダメです。
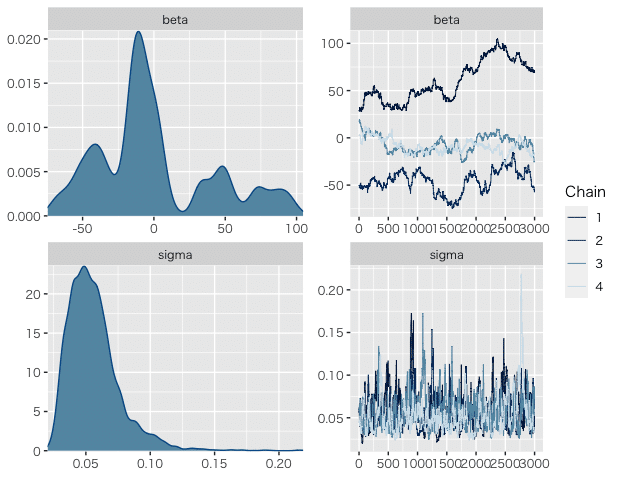
こんな感じでうまくいかなかったので、ググってブログ記事Aにたどり着いた、という経緯でした。
よくよくコードを眺めてみると、ブログ記事Aと私のStanコードの違いって、区画ごとに固有のrの合計を0にしたかどうかだけ、ということに気が付きました。場所差rの合計=0という制約を付けないと、全区画共通のβの推定も安定しないということでしょうか。
試しに私のコードにもr0を導入して、sum(r)=0になるように修正してStanを実行したところ、ちゃんと収束してブログ記事Aと同じような結果が得られました。
やはり区画ごとに固有のrの合計を0にすることが必要なようです。
終わりに
ということで、緑本第11章をRとStanでやってみる、ことは一応できたかなと思います。
一方で今回やってみて、警告メッセージへの対応をもっと勉強する必要があるなと感じました。公式ドキュメントによると、Stanは「積極的に」警告メッセージを出す設計になっているらしく、警告メッセージが出たことが即「何か問題がある」「結果が信頼できない」ことを意味するわけではないようです。
それでもせっかくNotifyしてくれているのだから、適切に対処できるようにはなりたいなあと思いつつ、これで締めたいと思います。
最後までお読みいただき、ありがとうございました。
この記事が気に入ったらサポートをしてみませんか?
