Excelのマクロを使って遊んでみた

どうも。そろそろテストが近いのでnote毎日更新一旦やめようかなと思っている筆者です。例によってゼノブレイドの進捗がなく、かといって麻雀ネタは人を選ぶので、あんまり連続で書きたくないと思って、話のネタになりそうなものを探していったところ、こんなものを見つけました。

「懸賞金1億2000万円」音楽系の企業が、数学の未解決問題に　なぜ？

なにこれ面白そう。もちろんこの問題を解いて懸賞金ゲットだぜ。を目指すわけではありません(バイトした方が絶対稼げる)。ただちょっと身近な数字を使って、本当にこうなるの？と確かめてみたくなりました。が、手計算は面倒くさいので、Excelのマクロ使えばいいんじゃね？記事のネタになるし一石二鳥じゃんと思った次第です。早速解説します。

(なお筆者はExcelのマクロは遊び程度しか使わないので、知識はあいまいだし、1ミリくらいしか使いこなしてません)

まずコラッツ予想についてです。どのような正の整数でも、偶数の場合は2で割る、奇数の場合は3倍して1を足す、という操作をして、出てきた数に対しても太字の操作をして、そのまた出てきた数に対しても…と繰り返すと、最終的に必ず1になるという予想らしいです。さあこれを1~100の正の整数でやってみたやつをマクロに実装してみましょう。

といってもいきなりはちと難しいので、まずは1つの正の整数にこの操作をすることを考えて整理してみましょう

①　好きな正の整数nを選ぶ。
②　nが偶数か奇数か判断する。偶数なら③-1、奇数なら③-2へ行く。
③-1　nを2で割る。その数を新たなnとする。②へ戻る。
③-2　nを3倍して1を足す。その数を新たなnとする。②へ戻る。

ていう感じですね。でもこれだと1になっても終わってくれず永遠に続く地獄が始まるので数が1になったらおしまいにしましょう。

①　好きな正の整数nを選ぶ。
②　nが1なら終了。そうでないなら③へ。
③　nが偶数か奇数か判断する。偶数なら④-1、奇数なら④-2へ行く。
④-1　nを2で割る。その数を新たなnとする。②へ戻る。
④-2　nを3倍して1を足す。その数を新たなnとする。②へ戻る。

さあじゃあ正の整数1~100まででこの操作をやってみましょう。

①　t=1　とする。
②　n=t　とする。
③　nが1なら⑥へ。そうでないなら④へ。
④　nが偶数か奇数か判断する。偶数なら⑤-1、奇数なら⑤-2へ行く。
⑤-1　nを2で割る。その数を新たなnとする。③へ戻る。
⑤-2　nを3倍して1を足す。その数を新たなnとする。③へ戻る。
⑥　tに1を加える。
⑦　tが101なら終了。100以下なら②へ。

もうここまで来たら、後は書くだけだ！！そして書き終わったものがこちらになります(一番わけわかんないところを飛ばしていくスタイル)。

Sub コラッツ予想()

Dim t As Long
Dim s As Long
Dim n As Long


t = 1

Cells.Clear


For t = 1 To 100

s = 1

Cells(s, t) = t

n = t

While n > 1

s = s + 1

If n Mod 2 = 0 Then

n = n / 2

Else

n = 3 * n + 1

End If

Cells(s, t) = n

Wend

Next t

End Sub

せっかくなので、ワークシートに途中経過を記述することにしました(詳しくは説明しない)。結果はこんな感じ。

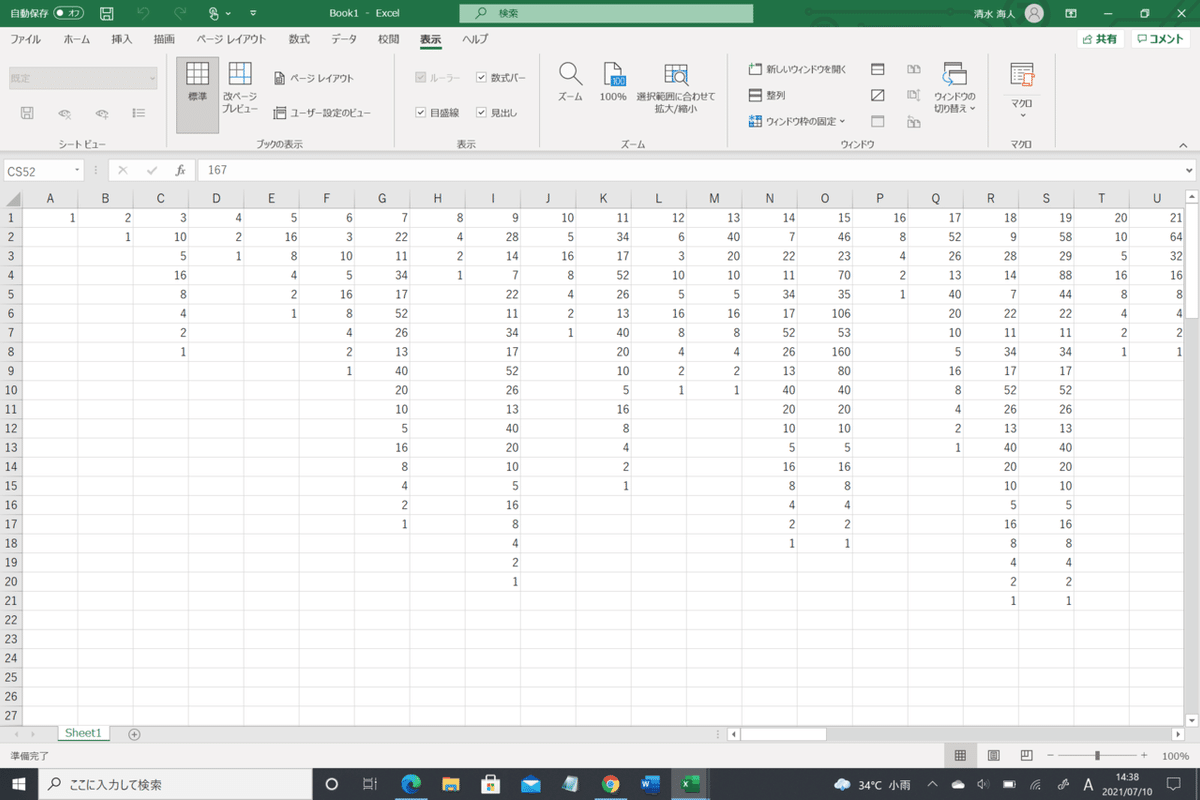
おぉーーー。このあとも100までちゃんと最後1になります。すごい。ちなみに97が一番1になるまで操作を繰り返すことが必要で、その回数は118回。さあここで遊びは終わりませんよ。まずは1000までやってみましょう。878で178回操作が最大でした。そんなに増えないのね。じゃあ今度は、3*n+1を変えるとどうなるか。ちなみに、最終的に1にならない場合、永遠の地獄が幕を開ける。5*n+1でそれは起こった。

見てもらえれば分かるが。26,13,66,33,166,83,416,208,104,52,26で循環してしまっている。なるほどですね。こうなってしまうと最終的に1になることは絶対ない。それが3*n+1で起こるかどうか。その答えはまだ分からないわけですか。いったいどうなるんでしょうね。まあでも遊びなので今日はこの辺で。