インバージョンの基礎理論③～非線形最小二乗法～(数式無し)【私の備忘録】

みなさん，こんにちは．
とある地学屋の日常ことゆうすけです．

　今回と次回は，地球物理学的観測データのインバージョンで一番よく使われる手法である非線形最小二乗法(Non-Linear Least Square Method) について説明していきます．今回は数式を用いずに説明していきます．

非線形最小二乗法によるインバージョンの概観

　非線形最小二乗法によるインバージョンのフローチャートを以下の図に示します．
　インバージョンにより最適なモデルを求めるときに，理論式が線形方程式で表せる場合(未知数の次数が1のときの方程式．例えば1次関数のような直線の方程式)は前回説明した最小二乗法で未知数(モデル)を求めることができます．しかし，理論式が非線形の場合は前回説明したような計算ではうまくいきません．
　前回説明した最小二乗法は，理論式を未知数で偏微分した際の結果が係数となる場合に使用することができます．すなわち，ヤコビアン行列の要素全てに未知数が含まれず係数となる場合のみ使用できるのです．しかし，世の中の現象は線形方程式で表せるものばかりではなく非線形の現象も沢山あります．非線形の場合，未知数で偏微分した際に未知数が残ってしまう要素がでてきます．すなわち，ヤコビアン行列の要素に未知数が残っているということです．この場合，図3のフローチャートで示したような非線形最小二乗法という手法を用います．
　図3を見ながら非線形最小二乗法のインバージョンの計算手順について説明します．
(ⅰ)未知数にいれる任意の値(初期モデル)を決めます．初期モデルを基に理論値を求めます．
(ⅱ)理論値と観測値の残差を求めます．この時点で残差は大きい状態です．
(ⅲ)最小二乗法を用いて，モデルの修正量を求めます．
(ⅳ)新しく求めたモデルをもとに再び理論値を求めます．
→残差が小さくなるまで，(ⅱ)～(ⅳ)を繰り返し計算します．この反復計算をイタレーションといいます．

                            図3.　インバージョンの手順(非線形最小二乗法)

非線形最小二乗法によるインバージョンの適用例

　非線形最小二乗法によるインバージョンは地球物理学の多くの分野で使用されている解析法ですが，今回は，微動アレイ探査を例に説明していきます．微動アレイ探査は，地球物理学的手法を用いて地下構造を解明する方法である物理探査の一種で，常時微動と呼ばれる波浪や交通振動など常に発生している振動を受動的に観測し，地下のS波速度構造を求める探査手法です．地下のS波速度を求めることで地盤が硬いか軟らかいかを明らかにすることができます．これにより土木構造物の耐震設計に役立てることができます．微動アレイ探査の初期モデル作成には，層数・層厚・S波速度を与える必要があります．層厚とS波速度は，経験則から与えることができますが，既往の情報があるならば，それを初期モデルの参考資料とするのがベストです．既往の情報は，ボーリングの地質柱状図やPS検層結果，反射法地震探査結果が挙げられます(図4)．

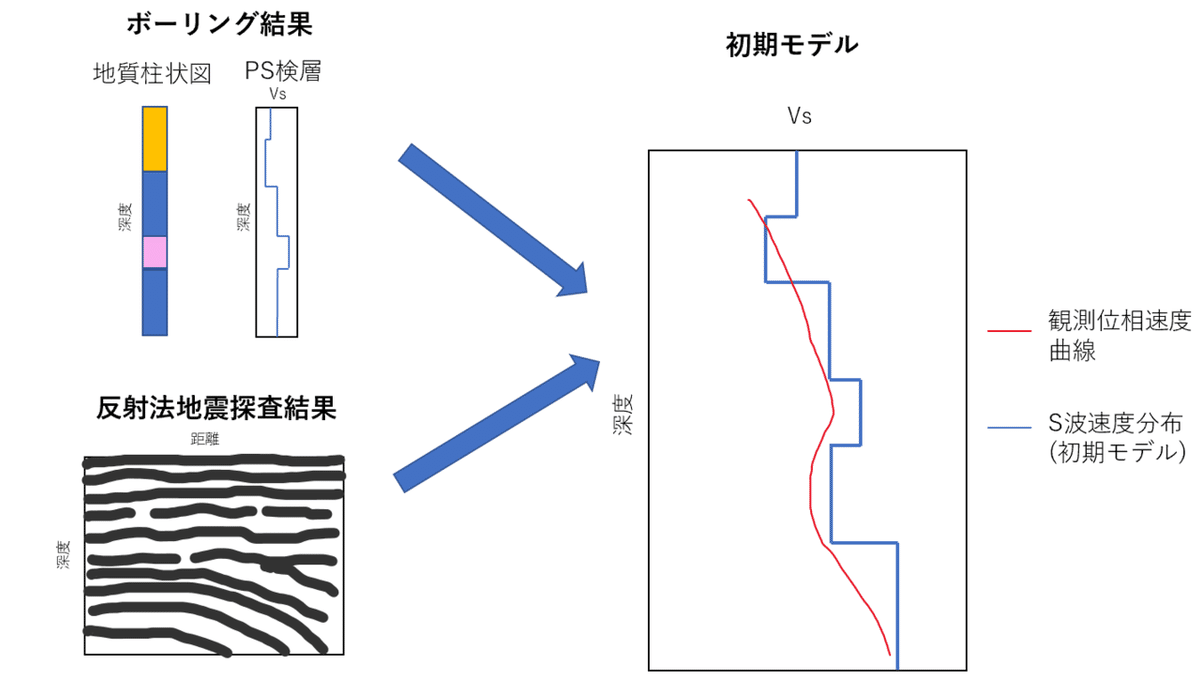
　図4.　微動アレイ探査における初期モデル作成のイメージ

　作成した初期モデルから，非線形最小二乗法によるインバージョンを用いて位相速度の観測値と理論値の残差が小さくなるようなS波速度構造を求めます．
 　インバージョンで求まるS波速度構造は作成した初期モデルによって様々です．解は無数に出てくることになります．解析者はいろんなパターンで初期モデルを作成し，いくつも出てくる複数の解の中から最も最適な結果を採用します．どのような初期モデルを作成すればよいのか？反復計算は何回実施するか？どの結果を採用すれば良いのか？などを判断するのは解析者の腕の見せ所であり，「こうすればうまくいく」というセオリー(Theory)は存在しないのです．これが地球物理学の解析で難しい問題であるのですが，ああでもない，こうでもないと考えたり，技術者同士で議論し合うのはやり甲斐のある仕事ではないかと思います．

　次回は，非線形最小二乗法によるインバージョンの計算手順について，数式を用いて説明します．新しい解析方法の説明ですが，前回説明した最小二乗法が基礎になっていますので，あまりビビる必要はないと思います．
次回もお楽しみください！

補足

・PS検層：ボーリング孔内にセンサーを挿入し，上下に移動させながらボーリング孔に沿ったP波速度及びS波速度を求める測定法です．振源と受振器を一体化させたセンサーをボーリング孔に挿入するサスペンション法，地表で振動を発生させてボーリング孔に受振器を挿入するダウンホール法の2種類が主に使われます．

・反射法地震探査：地表で人工的に地震波を発生させ，地下から跳ね返ってくる反射波を観測して地下構造を求める方法です．地震波の発生源が海上の場合は音波探査と呼ばれます．活断層調査，石油探査，火山体構造探査などで使用されます．