
株価はランダムなのか? その3
前項で以下を得たのでその続き

積分
(20)のexpの中を以下のように変形する。

これを用いると(20)は

になる。
先にκでの積分を考える。見やすくするため
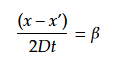
とおく。
定理:



erf: 誤差関数
(23) (24) (25) (26)を用いて(22)のκに関する積分は以下となる。

都合よく虚部が消えてくれた。 (22)に代入して

を得る。
δ関数
t=0のときの株価を$${s_0}$$として、その対数をμとする。

初期位置は決まっているので$${p_0}$$を以下のδ関数とする。

(30)を用いると(28)は

となる。平均がμ、分散が2Dtの正規分布になった。

以上を視覚化したのがこの動画
14:00くらいから
対数正規分布
(31)は株価sの対数であるxの関数となっている。これを株価sの関数にしたい。 (31)のxをlog sに置き換えるだけでは意味をなさない。確率密度関数pの単位は(確率/株価の対数)であるのに対して株価sの関数とした場合は(確率/株価)となるため。つまり密度の分母が異なる。
よって株価sを変数とする確率密度関数をfとすると、変換のための微分をpにかけて
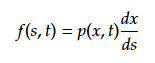
となる。 (1)より
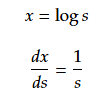
を用いて

を得る。確率密度関数fは対数正規分布となった。
参考文献
その4に続く
