チ。 ―地球の運動について―　火星の見え方

放送中のアニメ「チ。―地球の運動について―」が面白い。真理の探究を止められない、地動説を開拓していった中世の人々を描くフィクションだ。

日常生活で星の見え方なんて気にしたことはないな。現代人は星を見ることがあまりないけど、昔の人が夜見るものと言えば天体くらいしかなかったから星の動きに関心を持つのは自然なんだろう。

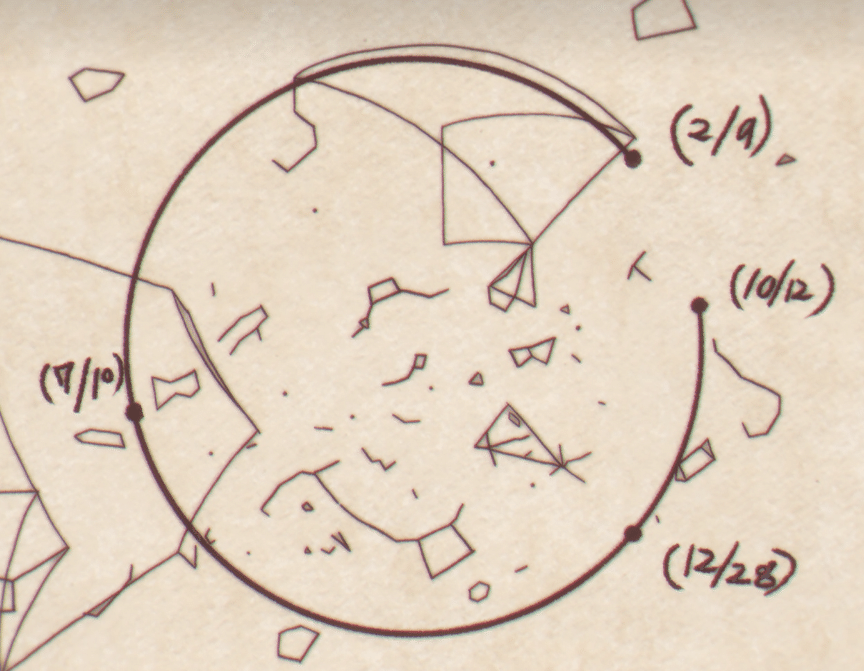
登場人物の一人、グラスさんが火星を観測していて火星の軌道が円を描くといってたのが気になった。

Fig.1　火星の観測
© 魚豊／小学館／チ。 ―地球の運動について―製作委員会

なんで円？　星は東西方向に動いて曲線にはなるけど円ではなくね？と思ったが、よく見ると星座との相対位置で天球にプロットしたものみたいだ。

Fig.2　火星の逆行
© 魚豊／小学館／チ。 ―地球の運動について―製作委員会

観測していたら逆向きに動き出したとかでショックを受けていたグラスさん。

火星が逆向きに動くように見えるのか簡単なモデルで考えてみる。

前提

Fig.3　記号は以下で記載

簡単にするため地球も火星も円軌道で、火星の公転面は地球の公転面に対してy軸周りに$${θ_{tm}}$$傾いているとする。公転軌道とy軸との交点を春分・秋分とする。

Fig.4　記号は以下で記載

地球表面での位置を極座標で表し、自転軸はy軸周りに$${θ_{te}}$$傾いているとする。地球の動きはこんな感じ。

Fig.5

火星の位置

まずは火星の位置を求める。

Tbl.1

時刻をtとすると太陽を原点とする火星の位置は

(1)

となる。以下の行列を用いて

(2)

軌道の傾きを考慮すると

(3)

になる。

観測者の位置

次に地球上の観測者の位置を求める。

Tbl.2

とすると、太陽を原点とする地球の位置は

(4)

となる。一方、地球表面での位置は

(5)

で表される。以下の行列を用いて

(6)

自転軸の傾きを考慮すると、地球表面での観測者の位置は

(7)

となる。 (4) (7)より太陽を原点とする観測者の位置は

(8)

となる。

天球上の火星の位置

観測者から見た火星の位置は

(9)

となる。よって観測者からの火星の方向は

(10)

で表される。

Fig.6

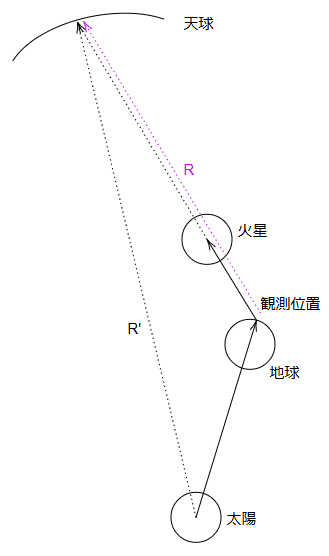
観測者から見た天球上の火星の位置は

(11)

であるが、天球は無限に遠いとするので

(12)

であり、原点(太陽の位置)と観測者の位置は同じと見做せ、季節毎に星座の位置関係が変わるといったことはなく、向きだけ考慮すればよい。したがって

(13)

として天球上の火星の天頂角θと方位角φは以下となる。

(14)

火星の見え方

天球上の位置が分かったのであとは計算するだけ。

t=0で夏至、地球と火星に位相差がないとする。
地球の公転半径を1.5億km、火星の公転半径を2.28億km、地球の公転周期を365日、火星の公転周期を687日、地球の半径を6400km、地球の自転周期を365/366日、地球の自転軸傾斜角を-23.4°、火星の軌道傾斜角を1.85°、観測は午前零時とする。またP王国はポーランドっぽいので観測者の緯度は北緯52°とする。

以上より計算したらそれらしいのができた。

Fig.7

Fig.8

グラスさんの日記に近くなるようにレーダーチャートにしてみる。

Fig.9

Fig.10

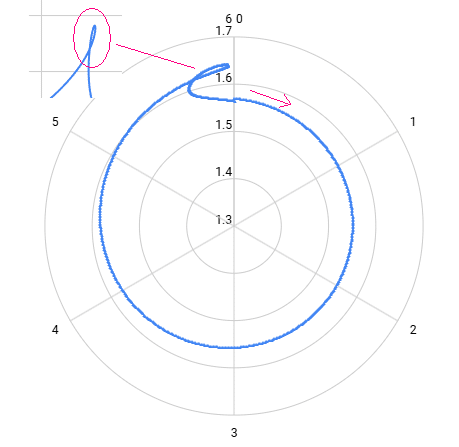
円になるか？と思ったらならない。昔の人には何が何だか分からなかったんだろう。

バデーニさんが七、八話で出した問題には楕円とか自転軸が傾いた球が公転していると思われる図が書いてあった。この記事のように自転と公転を組み合わせた系からの観測の問題だったのかな。地球以外から天球はどう見えるのか？という感じなのか。

それを半日で解いたヨレンタさんすげー。パソコンも使わずに手計算で半日とは恐ろしい14歳だ。