【34日目】100日後にベイズ統計ができるゆーみん

こんばんは！
今日から作業時間を計測してみます。
忘れないようにしないと！

さて、今日のご報告です。
アヒル本12章の続きです。

12. 5　時間構造と空間構造の等価性
今回は
❶ 状態空間モデルの理解を深めるためにモデル式↓の対数事後確率の数式を求める。

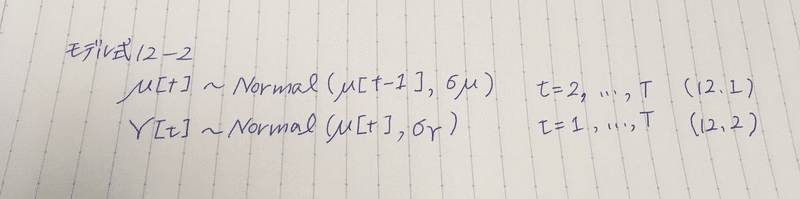
❷ 対数事後確率の視点から時間構造と空間構造の等価性を理解する。

です！今日はやばげな感じだ......

----------------------------------------------------------------

❶ 状態空間モデルの理解を深めるためにモデル式の対数事後確率の数式を求める。

1：システムモデルの事後確率を数式で書いて変形する

......わかったふりはできる。

正直よくわかりません😭

なので今回は助っ人を呼びました。父です。

父「σは下げて書け！6に見えるやろ💢」
最初からプリプリ怒っていましたが、丁寧に教えてくれました。

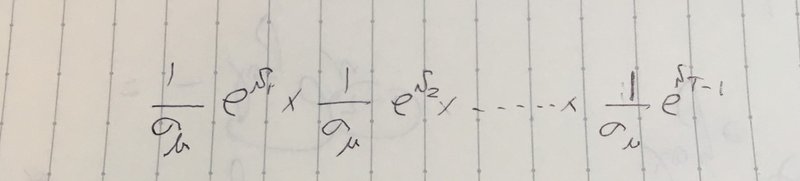
式を簡略化するとこのように書けます。で、

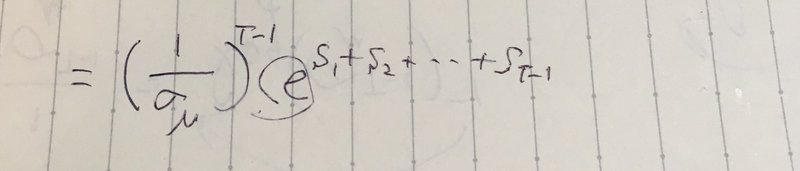
1/σμをまとめます。これはTー1個分掛け算したことになります。
この簡略化して書いたeの部分は底が同じなので指数部分は足し算となります。で、

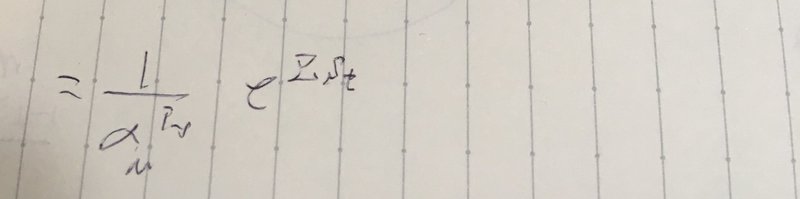
それをΣで書くとこうなる↑わけですね！理解理解！

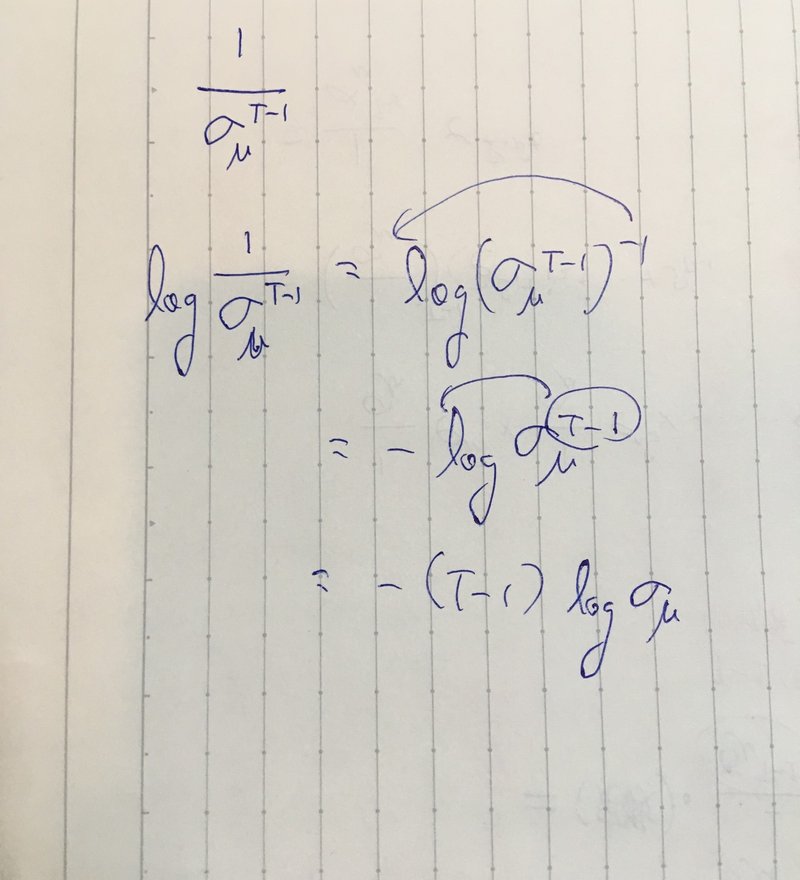
今度はこの式の対数を取ると以下の式になるそうです。

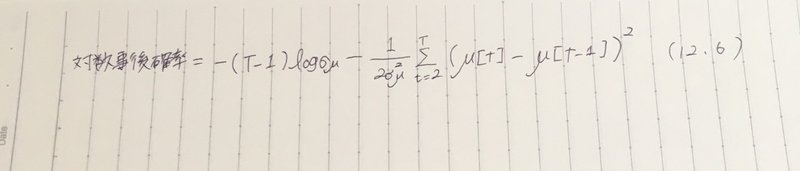
これも懇切丁寧に解説してくれました（呆れ顔でした）

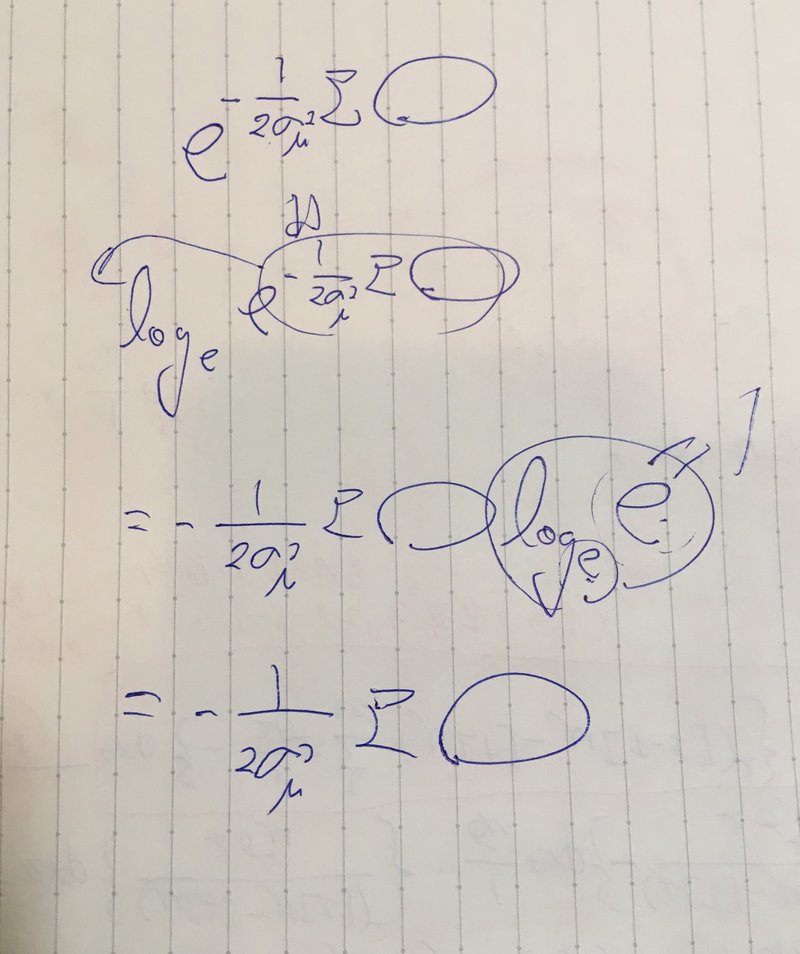
※Stanでは対数事後確率の偏微分が重要なので、偏微分で消える定数項は無視

2：観測モデルの事後確率を数式で書いて変形する

これはさっきと同じ計算方法なので大丈夫ですね！

ここからアヒル本では直感的に理解できるような説明がなされていました（父はお風呂に向かいました。ありがとう。）

・状態空間モデルではどのようにμ[t]が決まるか？

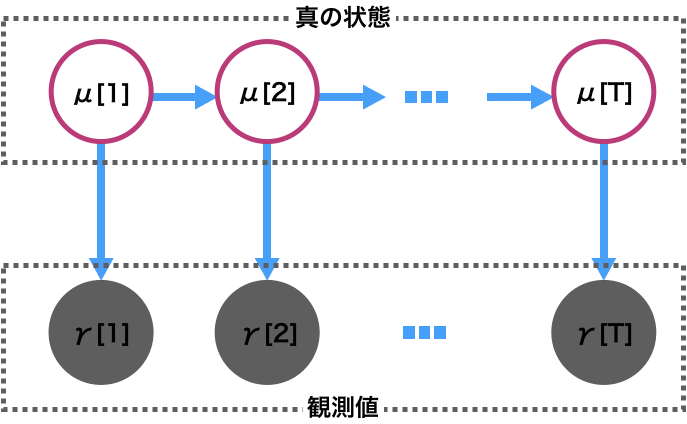
・システムモデルの対数事後分布だけをできるだけ高くするμ[t]を求めるには？
→ μ[t]とμ[t-1]をなるべく近づければ良い！つまり、μ[1]＝μ[2]...＝μ[T] でμ[t]が横一直線になる場合ですね。

観測モデルの対数事後分布だけをできるだけ高くするμ[t]を求めるには？
→ γ[t]とμ[t]をなるべく近づければ良い！つまり、γ[1]＝μ[t] (t=1,...,T) でμ[t]が折れ線グラフと一致してジグザグになる場合です。

つまり、状態空間モデル全体の対数事後確率（12.6式と12.7式の和）をできるだけ高くするμ[t]は、システムモデルと観測モデルの相反する条件のバランスで決まります！
※ なお、弱情報事前分布を入れることでこのバランスに手を加えることができるそうです。詳しくは12. 8節で！

❷ 対数事後確率の視点から時間構造と空間構造の等価性を理解する。

12. 6式の↓

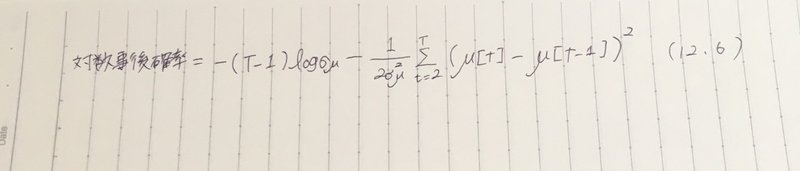
ここ↓

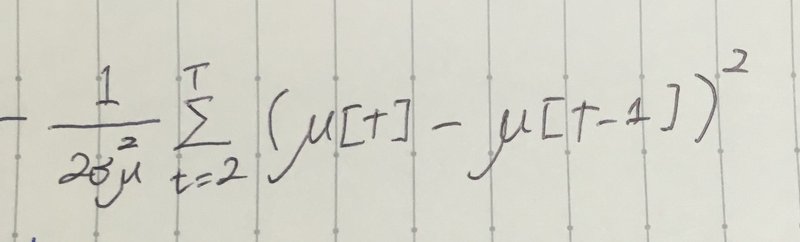
 μ[t]とμ[t-1]はひっくり返しても対数事後確率は同じ値である。
なので、t-1 からtへの向きはなく、「μ[t-1]とμ[t]は繋がっている」という見方ができる！この繋がりは「バネ」とみなせるそうです（？）

アヒル本図12-6を真似て描きました↓

バネの伸びをxとする。
バネの持つエネルギーはax^2と表す（ここで係数aはバネの固さを決める）。
エネルギーは小さいほうが安定であり、バネは持っているエネルギーを小さくするために伸びたら縮もうとする。つまりバネの伸びxを0にしようとする。
このエネルギーax^2を下げようとする挙動はμ[t-1]とμ[t]の差を小さくして、

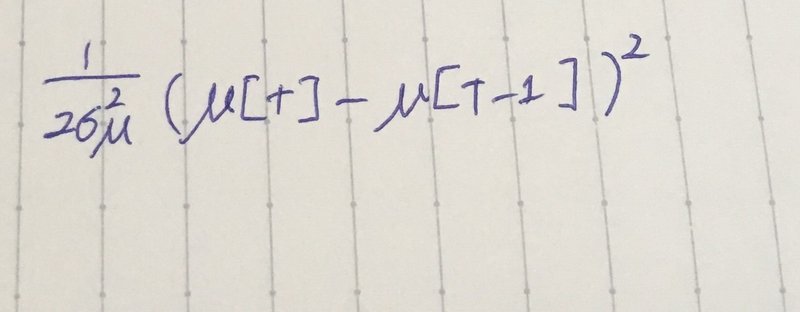
を下げよう、つまり対数事後確率を上げようとする挙動と同じになる！
μ[t-1]とμ[t]の差はバネの伸びに相当するのである〜

これらの理由から、
「繋がれている2つの要素はお互い引っ張りあって近い形になるはずだ」
という過程が背後に考えられる。

また12.6式に戻りますが↓

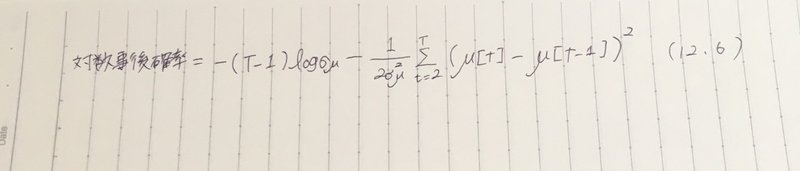
σμがバネの固さを決めています。
σμが大きい場合は柔らかいバネ、
σμが小さい場合は硬いバネ　に相当する。

12.6式の第一項はバネが柔らかすぎる場合にペナルティを課す意味になっています。

先ほどは「 μ[t]とμ[t-1]はひっくり返しても対数事後確率は同じ値である。
なので、t-1 からtへの向きはなく、「μ[t-1]とμ[t]は繋がっている」という見方ができる！」といってきましたが、状態空間モデルは「ノード（要素）」に注目する見方なので、t-1 からtへの向きがあります！！

なのでこのようなバネの見方は「エッジ（つながり）」に注目する見方であり向きがない。このような繋がりから対数事後確率が定まるモデルをマルコフ場モデルやマルコフ確率場と呼びます。

状態空間モデルとマルコフ場モデルの記法は対数事後確率の点からは等価なので、時間構造のように有向なものと、空間構造のように無向なものを同じ式で扱うことができます。

「向きがない」と考えていることを強調したい場合は、モデル式12-2↓

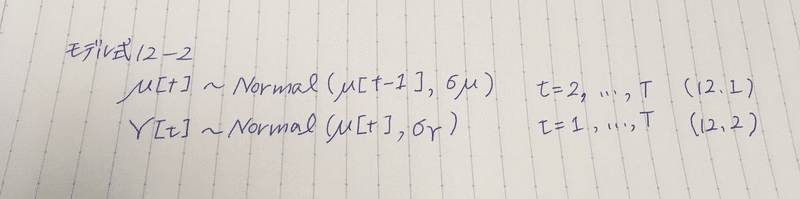
の代わりに、同時分布を用いて以下のように書く↓

A：すべての繋がりの個数（バネの個数）

12.8式のお気持ちを表すと「μ[1]μ[2],...,μ[T]の同時分布 p(μ[1], μ[2],...,μ[T]) （に比例する量）を右辺で定める」という意味である。

Stanコードにおいては、向きがないのを明確にするため、targetを使った記法とnormal_lpdf関数を用いて以下のように書くそうです↓

target += normal_lpdf(mu[2:T] | mu[1 : (T-1)], s_mu)

最後に強調していましたが、
記法は変化しても最終的な対数事後確率は同じある、ことが重要だそうです。

今日はここまで！
私のあまりの数学のできなさに父が幻滅しておりましたw
夏休みに高校数学を特訓していただくこととなりました（）
「社会科学のための〜」の数式を噛み砕いたブログを書いてもいいかもしれません。やろうかな？？？どうでしょうかね。

ではまた明日お会いしましょう！

あと66日