［高校数学］三角関数 加法定理の派生公式を即席で作る方法

　加法定理の派生公式は暗記する必要はなく、その場で作れればいい。作り方とコツのほうを覚えておこう。

基本公式は覚える

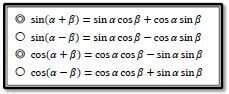
　↑出発点なので、すぐに思い出せるようにしておく必要があります。試験のときは、この基本４式を問題用紙の余白に書き出して準備です。

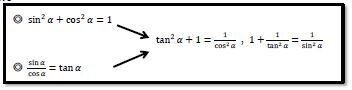
　↑こちらも使うので確認です。◎は覚えておいて、右側はすぐに作れるようにしておきましょう。

Ⅰ 加法定理 ―加法定理基本４式から、 𝐭𝐚𝐧(𝜶 + 𝜷)， 𝐭𝐚𝐧(𝜶 − 𝜷), 𝐭𝐚𝐧 𝟐𝜶 へ

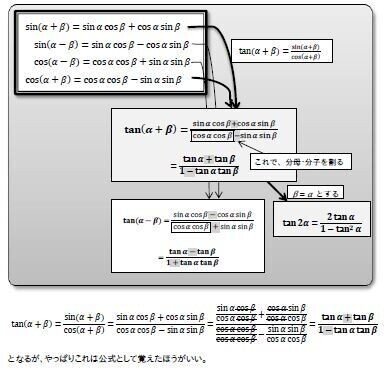
　作るのがやや厄介なので覚えておいたほうがいいかもしれません。ただし、分子に＋、分母にーが入る理由は、途中式をイメージできれば思い出せます。高校の先生が「タン プラ(ス) タン、１マイナス タン タン」と言っていたような⋯

Ⅱ ２倍角，半角の公式　―２次を１次にする、tan 𝑥/2で表す

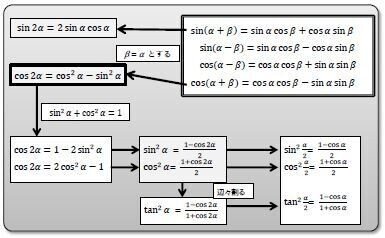
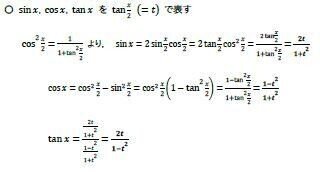
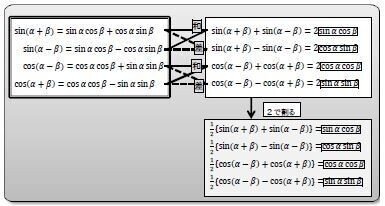
Ⅲ 積和公式ー 加法定理４式の右辺に求めたいものがある。

　sin 𝛼 cos 𝛽 = ⋯ , cos 𝛼 sin 𝛽 = ⋯ , cos 𝛼 cos 𝛽 =⋯ , sin 𝛼 sin 𝛽 = ⋯ の公式については、加法定理の式の右辺の中にあることを意識しておき、４式中の２式の和または差からすぐに作れることを覚えておけばよい。

Ⅳ 和積公式 ー 覚える必要も，公式自体の必要性もないが…

　三角関数の和を積にする変形のために下記のような和積公式があるが、実はそれらを使わなくても加法定理の基本4式で出来てしまう。但し多少のコツが要るので、具体的にやってみる。
　例えば、sin80°+sin70° の場合。

この方法は　sin どうしの和 ／差、 cos どうしの和／差のときには必ず使える。 一般的には

Ⅴ 三角関数の合成 ー 加法定理 sin(𝛼 + 𝛽) = … の逆演算として

Ⅵ ３倍角の公式　(あまり使う機会はないが)

微分・積分で 使う！

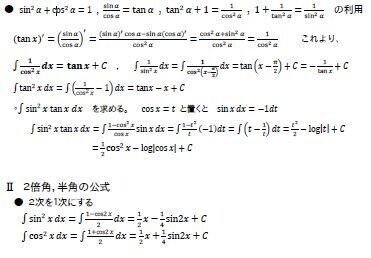
加法定理の式を導き出す

PDFダウンロード