温度変化に晒される磁石の磁化の臨界的振る舞い【論文紹介】#11

イジングモデルと、その2次元での厳密解が求まっていることは知っているものとする。
と言いたいが、私の論文紹介シリーズでイジングモデルが出てくるのは初めてなので概説する。(イジングモデルは、量子力学と同じくらい、大学で物理を学んだ者なら誰でも知っている前提知識のようなものだが。)

鉄が磁石になったものは分割しても両極を持つ磁石なのはよく知られているが、原子一個でも磁石の性質を持っている。
実は原子一個で磁石の性質を持つ元素は金、銀、銅、リチウム、ナトリウム、カリウム…など他にもたくさんあるが、大抵の元素では向きがバラバラになってマクロスケールでは打ち消しあって磁石にはならない。鉄のようにマクロスケールで向きがそろって強磁性を持つものは少ない。そのミクロスケールとマクロスケールの違いを分析するために単純化されたモデルがイジングモデルだ。

2次元イジングモデルの概略図
(https://app.journal.ieice.org/trial/103_3/k103_3_311/index.html)

2次元のイジングモデルでは、上図のように格子状に原子があり、それぞれのスピン(磁石の向き)が上向きか下向きかのどちらかになるとする。i番目の原子のスピン$${σ_i}$$は上向きなら1、下向きなら-1の値を取る。
スピンは、隣同士の磁場と外部の磁場と反応して、ハミルトニアンH(全体のエネルギー)は次のように考えられる。隣同士で向きが揃えばエネルギー的に有利(エネルギーが小さくなる)であり、隣合う$${σ_i}$$と$${σ_j}$$がどちらも1またはどちらも-1の場合、$${J_{ij}(>0)}$$だけエネルギーが減る、逆に$${σ_i}$$と$${σ_j}$$の向きが違えば$${J_{ij}}$$だけエネルギーが増える。それが図の下の式の右辺1項目。Σの下の<i, j>は隣り合うi, jのペア全てを足し合わせることを表す。
右辺2項目は、j番目の原子のスピンと外部磁場の向きが揃えばエネルギー的に有利で、$${h_j}$$と$${σ_j}$$の積の値だけエネルギーが減る(向きが同じなら減るが、向きが違うなら増える)ことを表す。
純粋で均一な原子配列なら$${J_{ij}}$$はi, jによらず全て一定のJで(これが原子の種類によって違う)、外部磁場$${h_j}$$も一定と単純化することも多い。
外部磁場$${h_j}$$はゼロであることもあり、外部磁場ゼロで、スピンがばらけようとする熱攪乱(温度)がある程度あっても、スピン同士の相互作用によって向きが1方向に揃ったままになる。しかもそれは、温度を下げればだんだんと揃うのではなく、図1の黒の点線に示すように、ある臨界温度を境にゼロから急激に立ち現れるのが驚くべきところであり、それが強磁性相転移と呼ばれる。その境目となる臨界温度$${T_c}$$は2次元イジングモデルでは次のように厳密に求められている。
$${T_c=\frac{2J}{k\cdot ln(1+\sqrt{2})}}$$ (kはボルツマン定数)
(ちなみに、3次元イジングモデルの臨界温度はシミュレーションでおおよその値はわかっているが、厳密解はまだわかっていない。)

さて、今週紹介する論文はこちら
Dynamic behavior of a Magnetic system driven by an oscillatory external temperature
振動する外部温度によって駆動される磁性体の動的挙動
2312.10164.pdf (arxiv.org)

磁性体をイジングモデルで表されるものとし、臨界温度Tc付近で振動するような温度変化を加えるとどのような振る舞いを見せるかを調べる。通常、イジングモデルは温度一定でシミュレーションするが、本論文では$${T(t)=T_0+A\cdot sin\frac{2πt}{τ}}$$と表される、中心T0、振幅A、周期τで振動する温度下でシミュレーションを行う。
粒子の数は1辺の粒子数Lが64~1024の、L×L の周期境界条件のフィールド、
振動する温度の中心T0は0.9Tc~1.2Tc、
振幅Aは0~0.5Tc、
周期τは4~256 MCs(モンテカルロステップ)とする。
シミュレーションの仕方は、L×Lの原子のうち1つをランダムに選び、そのスピンを反転させた場合のハミルトニアンの変化をΔHとすると、$${e^{\frac{-ΔH}{kT}}}$$の確率でスピンを反転させる(この確率が、スピンが揃おうとする傾向と熱でばらけようとする傾向の拮抗を表している)。この操作をL×L回行うのが1 MCs(モンテカルロステップ)である。

磁化Mを、全原子のスピンの平均値として次のように定義する。
$${M(t)=|\sum_i{σ_i}|/L^2}$$
温度振動が1周する間の平均磁化Qは、1周分の周回積分を用いて次のように書ける。
$${Q=\frac{1}{τ}\oint M(t)dt}$$

まず、粒子数L = 256、振幅A = 0.2Tc、周期τ = 64 MCsで振動の中心T0を変えてシミュレーションを行った結果が図1である。

図1　振動する温度下における磁化の変化
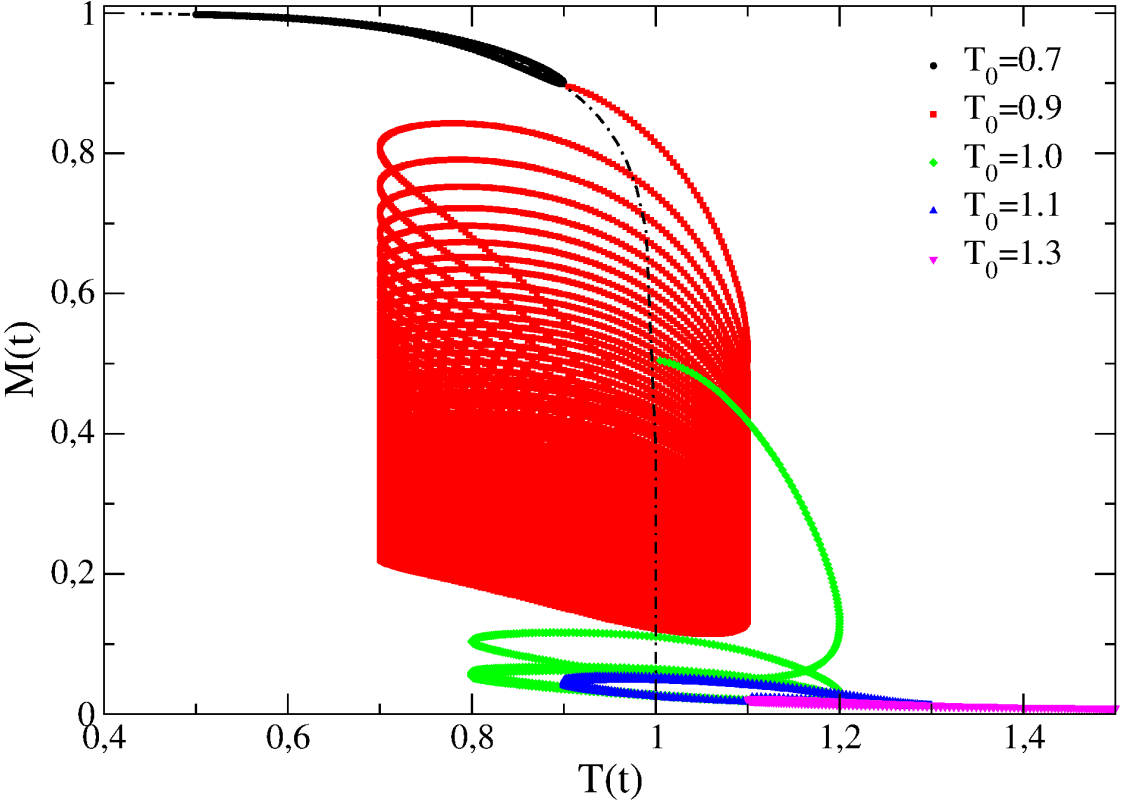
横軸の温度は臨界温度Tcとの比を表す
黒の破線は温度振動がない場合の理論値　臨界温度より低温では1に近い磁化を持つ(スピンがほぼ揃っている)が、臨界温度直前で急激に磁化は下がり、臨界温度を超えると磁化は0(スピンがばらばら)になる

振動の中心T0が0.7と1.3のときは、臨界温度から離れているのであまり面白いことは起こっていない。臨界温度を跨ぐ振動では、同じ温度でも行きと帰りで磁化が異なる履歴効果(ヒステリシス)が見られる。特に、0.9と1.0のときは、(最終的には定常的なループに入るのだが)初期位置から螺旋状に落ちていく軌跡が印象的な曲線を描いている。

次は、振動中心をT0=1.0Tcに固定して粒子数Lを変えてシミュレーションを行った結果が図2(a)。粒子数が少ないと、”画素が荒い”せいで理想とは遠い振る舞いになると考えられるので、粒子数によって差が出る場合は粒子数が多いほうが理想に近い振る舞いだと解釈する。図2(a)を見ると、振動中心がTcちょうどの場合は磁化はずっとゼロになるようだ。
続いて、振動中心がTcちょうどの場合で振動1周分の平均磁化Qを、粒子数Lと振動周期τを変えて調べたのが図2(b)と(c)。粒子数Lが大きくなればなるほど、周期τが大きくなればなるほど、平均磁化は急速に0に落ちていく。縦軸は対数軸なので落ち方は指数関数的でかなり急激である。そしてどちらの場合も、きれいに指数フィッティング(対数グラフ上での直線)に乗る。直線の傾きより、指数は
$${Q \propto L^{−α}}$$において、α≒1.0
$${Q \propto τ^{−β}}$$において、β≒0.70

図2　(a)粒子数Lを変えたときの最終的に落ち着く磁化振動のループ
(b)(c)粒子数L、振動周期τを変えたときの1周期の平均磁化Q

次に、粒子数Lは512と1024、周期τは64で、振幅Aを変えてみて平均磁化を調べたのが図3。

図3　温度振動の振幅Aを変えたときの平均磁化　0.03Tcより小さい振幅では0.2程度で概ね一定の平均磁化があり、それより大きい振幅ではe^(e^(-A))に比例して急激に平均磁化は落ちるように見える

興味深いことに、これは縦軸、横軸ともに対数軸にしても直線状にはならず、指数法則が見られない。
ここからは私の考察だが、どうやら振幅が小さい場合と大きい場合で別の2つの法則に支配されている。振幅Aが0.03Tcより小さいところでは平均磁化は0.2程度で概ね一定の値である。これは振幅ゼロのときとほぼ同じで、臨界温度より上のスピンがばらける影響はあまり受けない。振幅Aが0.03Tcより大きいところでは、縦軸が対数なのに指数関数的に減少する曲線となっているため、$${Q \propto e^{e^{-A}}}$$となる非常に急激な減少なのではないかと見て取れる。振幅が大きいと、高温側でスピンがばらける影響を強く受けるようになるために急速に平均磁化はゼロに落ちる、と定性的には考えられるが、定量的になぜ$${Q \propto e^{-A}}$$ではなく$${Q \propto e^{e^{-A}}}$$となるのかはわからない。
また、データ点がやや不足しているように見えるがこの抜け具合を見るに、計算量的にL=1024が限界だったと思われる。私も似たシミュレーションの経験があるのだが、臨界点近くの現象はとかく収束が遅い。おそらくこのグラフのプロット1点のQの値を出すのに数時間はかかっていると思われる(昼間にコードを組んで夜中に走らせっぱなしにして翌日に結果が出てたり出てなかったりする)。

最後に、初期温度T0を変えたときの平均磁化を調べた。
初期温度T0をいくつか変えながら振動周期τを変えると、τによって臨界温度Tcがわずかにだが変化するのが見られる(図4右上)。この指数は
$${\frac{T_c(τ)}{T_c} \propto τ^{−γ}}$$において、γ≒0.03

図4　温度振動の中心温度と平均磁化の関係
横軸は、τによってずれた臨界温度との差

図4の平均磁化のプロットを見ると、温度一定のときの理論値(図1の黒の破線)とかなり近い値であり、なんだかつまらない結果のようにも思えるが、面白いのはそこから温度振動成分ずれるときの指数法則の部分だと思う。
ここまで得られた指数法則をまとめると、平均磁化Qは、温度振動によってずれた臨界温度Tc(τ)、粒子数L、振動周期τの関数で次のように書ける。
$${Q(τ) = f(\frac{T0 − Tc(τ)}{Tc} , L^{−α} , τ^{−β})}$$
$${T_c(τ) \propto τ^{−γ}, α = 1.0, β = 0.70, γ = 0.03}$$
これらの臨界指数を出すのは、臨界現象についての研究の常套手段であるが、これだけではまだわからない。
しかし、他の臨界現象、例えば水が氷になる相転移や、水銀が超電導になる相転移や、感染対策の具合によって感染爆発が起こるか起こらないかの臨界現象など、全く異なるように見える現象にも意外に共通する臨界指数が見られ、同様な構造が見いだされることでさらに研究が深まるかもしれない。

イジングモデルはもはや数えきれないほど様々な角度から研究された論文が発表されているが、臨界温度前後で温度振動を加えるというのはシンプルながら今までなかった発想だと思われる。
特に、温度の振幅に関して平均磁化が単純な指数法則に乗らない奇妙な振る舞いを見せるというのは、イジングモデルのまだ見ぬ奥深さを垣間見ているようで興味深い。