
過渡カオス数列(仮称)の世界へのいくつかの入り口
Fly straight dammit! sequence(真っすぐ飛べこのっ!数列)という数列がある。この数列の説明は↓この動画の前半(1:33~7:49)を見てほしい。英語はわからなくても数字を見ればだいたいわかると思う(common factorは公約数、gcdはgreatest common divisor最大公約数のこと)。
この動画を見て私がまず思ったのは、数学的帰納法で「n=kで成り立つならn=k+1で成り立つと言っても、n=1のときで成り立つとは限らないのではないか」という長年抱いていた疑問の反例だと思った。
数学的帰納法で証明されるものは、nがマイナス無限大から成り立つもの、n=0から成り立つもの、n=1から成り立つもの、それ以外の数から成り立つものがあるように思うけど、この数列はそれ以外の数(n=638)から成り立つ、初めて見た例だ。
そして、この数列はスタートを1以外の数にすれば違った振る舞いが見られるのではないかと思った。
今回は、前に書いた『またりさま』の解釈みたいな、たまに投下する単発ネタ!(過去に別のところに書いたものの移植記事ですが)
『またりさま』のセルオートマトン的解釈と変奏(1)|喜多見奈美 (note.com)
(『またりさま』も(3)の内容の計算が膨大になって止まっているけど、続きを書かねば)
Fly straight dammit! sequenceは、Excelで簡単に再現できる。
まず、1から作りたい長さまでの整数列をA列に用意し、B列の1番目に1を置く。
B列の2番目以降は、左と上の最大公約数が1なら二つを足して+1する。最大公約数が1でないなら上の数をその最大公約数で割る。IFとGCD関数で簡単にできる。
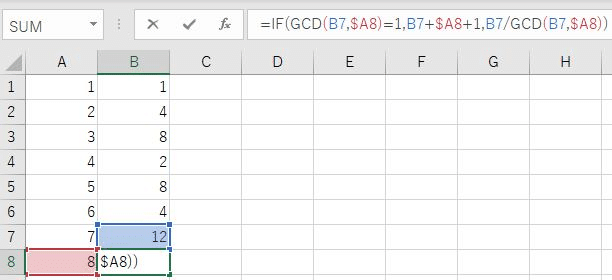
これを700項くらいまでがーっとドラッグして散布図を作ると、動画のとおり、638項目でいきなり揃うグラフが得られる。

ここまではまあ予想通りで、面白いのはここから。
スタートの数(B列の1番目)を今度は1から2に変えてみると、得られるグラフががらりと変わる。

見事に最初からきれいに真っすぐ飛んでいる。Fly straight dammitとは微塵も感じない。
同様に、初項を3にしてもきれいにまっすぐなグラフが得られる。

どうやら、初項1のときがかなり奇妙な特殊パターンだったようだ。
初項を4にしてみると……これは?

ほんの少しだけ乱れてから安定状態に入っている。

もう少し詳しく見ると、初項が4だと36項目から定常振動に落ち着くようだ。
初項を1から8まで変えた数列を横に並べて、数の大小を色で表してみたのがこの図。

何やら、収束の仕方にいくつかパターンがあるようだ。まず真ん中で目立つ初項4,5,6の列では、10項目に3になって以降同じ振る舞いだし、その両隣の初項3と7は、16項目に1になって以降同じで、36項目で1になってからは初項4,5,6の列と合流している。
さっき同じに見えた初項2と3は最初から周期4の定常振動に入っているが、初項4,5,6,7が合流する初項3と初項2の列は逆位相の振動で合流しない。
そして、奇妙に見えた初項1の列は、早くも2番目で4となる初項8の列と同じ振る舞いになっている。
同様の見方をサイズを広げてやってみた。
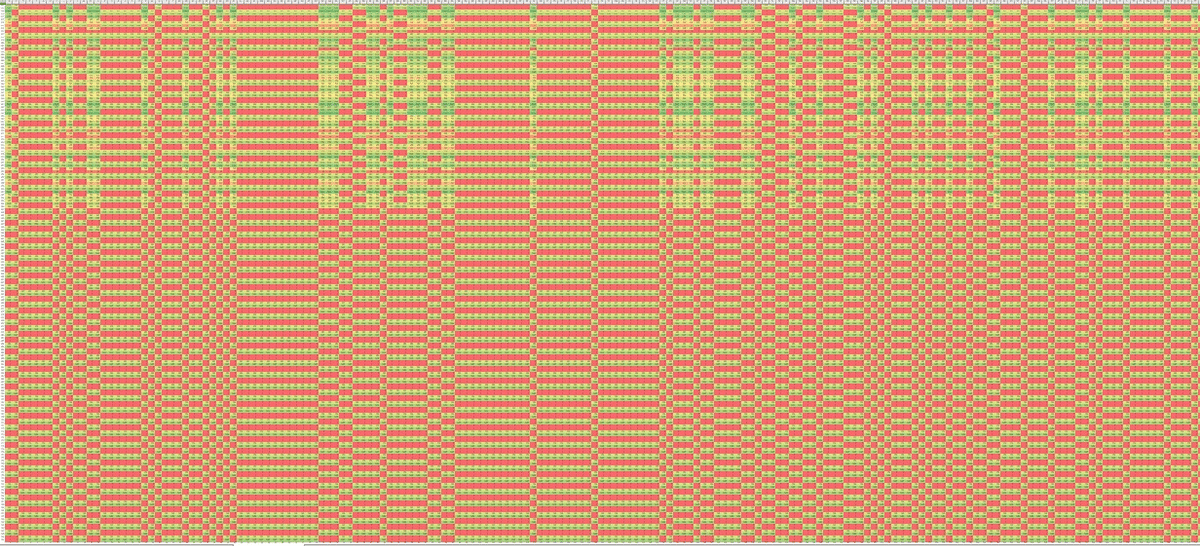
一番下は750項目までで、初項(横)は360までやってみた。
どうやら、1や8と同じ638項目で収束するものとそれより早く収束するもの、またその中にも逆位相のものが存在するように見える。
その3つのグループ分けをしてみたのが次の画像。

画像は入りきらなくて右に寄っているが、初項3,4,5,6,7と同じ収束の仕方をするものが最多で、360列のうち225列。その逆位相が35列、初項1,8のように638項目で収束するものが100列となった。収束する直前の637項目の値が11か2か639かでここのグループ分けはできる。
さらに細かく上のほうまでグループ分けをしていった結果が次の図。

数列の作り方としては上から下への不可逆演算だが、逆に下から上にたどると見ると、次々に枝分かれしていってそれぞれの数(1から360までは全ての数)にたどり着くのが見て取れる。
このような、枝分かれをたどっていくとある数からどんな数へもたどり着くというのは、別のところでも見たことがある。(関係ないと思っていたもの同士に、意外なつながりをふと見つけるのは数学にたまにあることだが)
コラッツ予想だ。(こちらも説明は↑この動画に任せるが)
こちらは、一定の操作でどんな数でも1にたどり着くかという問題で、あらゆる数が、1本の川に次々合流していくように見える(「どんな数でも1にたどり着くか」という問題は未解決だが)。Fly straight dammit! sequenceと同様に、あえて逆にたどってみて1から枝分かれを作っていってどんな数にもたどり着けるかという考え方もある。
Fly straight dammit数列も、「どんな数でも定常振動に落ち着くか」という問題は未解決かもしれない。
1つ推測できることは、638項目でも収束しない最初の反例は、2^600くらいのオーダーかそれ以上になると思う。これはつまり、数列が1つ進むごとに2くらいで割っていって638項目までに1にまで小さくできるかという大雑把な推測だ。
残念ながら、Excelでは反例になるほど大きな数は探せないし、そこまで全て638項目までには収束するという前提を踏まえ、638項目で収束しないと言っても、もう少し先でやっぱり収束するかもしれない。「どんな数でも定常振動に落ち着くか」という問題は非常に難しい問題だと思える。
あるいは、Fly straight dammit数列はラングトンの蟻と似た振る舞いと言えるかもしれない。(これも説明は動画に任せるが)
これは初期状態に障害物があっても、十分時間が経てば、規則的にまっすぐ移動していくHighway状態に落ち着くという。
ここまで見てきたFly straight dammit数列、コラッツ予想、ラングトンの蟻に共通することというと、最初のうちは不規則な動きだが、ある程度時間が経てば安定した挙動に落ち着くということ。
これら3つが本当に関係あるかは不明だが、振る舞いとしては「過渡カオス」に似ていると言える。
過渡カオスの一番わかりやすい例はサイコロであろう。サイコロを投げた後、最初の着地でサイコロの角と床の衝突角度によって跳ね返る向きと角度と回転が決まる。ここで重要なことは、着地時の角度が少し違うだけで、次の着地時の角度が大きく異なる。その次の2回目の着地でもサイコロの角と床の衝突角度によって跳ね返る向きと角度と回転が決まる。
着地するごとにわずかな誤差が増幅される。初期値鋭敏性を持つのである。(これが、サイコロでほぼ予測不能な目が出る理由である)
その次の3回目の着地でも、4回目の着地でもと何度か着地するうちに弾性によって跳ね返りが小さくなってやがて止まるので、天気のように永続するカオスではない。このような過渡的な部分だけカオス的な振る舞いがみられる現象を過渡カオスと言う。
他にも、過渡カオスの説明はこの記事が詳しい。
Fly straight dammit数列やコラッツ予想は(暫定的にでも)「過渡カオス数列」と呼んでいいかもしれない。(なぜ過渡カオス的になるのかや、この呼び方が本当に適切かどうかは不明だが。)
コラッツ予想に関して、ポール・エルデシュは「数学はまだこの種の問題に対する用意ができていない」と言ったそうだが、過渡カオス系だと思えば行けそうな気がしなくもない。
数列は離散的なので、実数に拡張して、既知のものと一致する臨界指数やファイゲンバウム定数などが出てきたりはしないだろうか。
残念ながらそこまで研究するのは私には難しそうだが、過渡カオス数列という概念は提唱したい。
(追記)
Fly straight dammit数列が「どんな数でも定常振動に落ち着くか」という問題に関して、
>638項目でも収束しない最初の反例は、2^600くらいのオーダーかそれ以上になると思う。
と書いたが、意外にも早く638項目で収束しない反例を発見した。
初項が50003507と50004499のとき、収束するのは638項目ではなく651項目になる。

上図は、651項目で収束する列(651系)2つと、比較用に近い初項で638項目で収束する列(638系)と正位相で収束する列の比較。グラフの縦軸は対数。
今回新たに見つかった651系である、初項50003507と50004499の列は15項目で合流し、651項目で初めて638系と合流する全く新しい別系列である。
(このグラフの序盤で急激に下がるところはだいたいn番目でe^(-0.5n)のオーダーで収束していく。この対数グラフ上の直線が638項目になっても1に達しないくらいスタートの数を大きくするというのが当初の推測の2^600とかいう値。推測よりめちゃくちゃ早く見つかった。)
また、この新しい系列の発生とそれに伴う(ように見える)奇妙な現象も発見した。
下図は初項を1桁ずつ増やしていったとき、正位相、逆位相、638系、651系の現れる頻度(10000のうちいくつあるか)を調べてみたものである。

横の値3以上は、初項が10の何乗かの値
初項3,4,5,6,7のような収束をするものを正位相と呼ぶが、最初は正位相が最多数派、次が638系、逆位相が最少数派なのは既に見たとおり。数を大きくしていくと収束しにくくなって638系が多くなり、そのうち新しい系統が現れるのではないかと当初は思っていた。初項10^5程度で638系が最多数派となったが、その後、10^8くらいでまた割合が元に戻るのと同時くらいで新しい651系が現れるという謎現象が見られた。
そして逆位相と651系がじわじわと伸びてきて、初項10^15で638系より逆位相が多くなった。(なぜこのような増減になるかは全くわからない。)
(というか、651系の存在は知らない時点で、3つのグループの頻度を調べてみようという動機からこのグラフを作ったほうが先。10^8から合計が10000にならないところから651系を発見した。50003507と50004499は50000000というキリのいい数に近いから最初に見つかった反例であって、最も小さい反例かはわからない。)
(追追記 2024/10/29)
最小の651系は初項27247147
ちょっと計算を効率化したらいけた。
にしても、ポリア予想並みにでかい反例だ。
次は651でも収束しないものを探そうか。理論上、新しい系列はlogNのオーダーだけど無数に現れると推測できる。
(追追追記 2024/10/30)
なぜか飛び地的に、桁違いに小さい651系を見逃していた。初項が以下の4つがなぜが飛び地的で最小の651系。
3500845
3500887
3500966
3501019
