ダイポールアンテナの八の字特性
今日、ちょうど電磁気学のリハビリに良い演習問題があったので、解いてみました。電磁気学をやっていれば、どこかでやっているはず、の問題です。
【今日の教科書】
・今井哲朗, "電波伝搬解析のためのレイトレーシング法", コロナ社(2016)
(3.25)式において、微小ダイポールアンテナの電場において、ダイポールアンテナの球面座標で言う二つの角度座標系(φ, θ)では、そこで発生する電場はφには依存せず、sinθに依存する特性を持つ、と言う式があります。今回は、この式を復習がてら示します。
・砂川重信, "4-物理テキストシリーズ 電磁気学", 岩波書店(1977)
私の中では、電磁気学のバイブルです。大体の基礎理論はここに書いてます。今回は電気双極子の式を利用します。
【ダイポールアンテナとは】
一軸に対して一定の長さdを持つようなアンテナをダイポールアンテナといい、ダイポールアンテナの両端に電圧を加えると、電荷分布が発生します。
そこで、両端のアンテナに電子が振動すると、あたかも電気双極子が主要因となり電場を発するのですが、電場分布は上記サイトにあるように八の字の特性を有します。
【計算】
この電気双極子が発生させるポテンシャルは、Coulombの法則を近似的に演算すると、電気双極子に変換された形で演算できますので、今回はそこで得られているCoulombポテンシャルを利用して計算してみました。
今回使用するCoulombポテンシャルの式
![]()
![]()
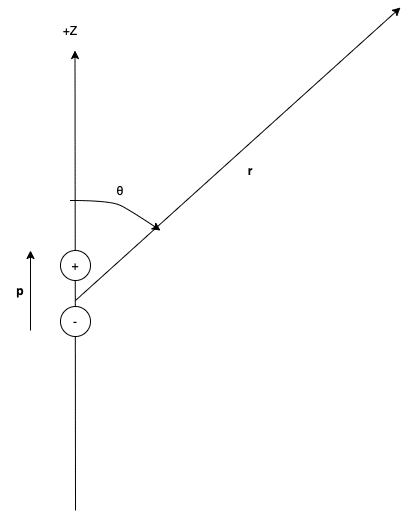
直流で励起される電気双極子pが位置rにあるとし、電気双極子は空間に対して十分小さいものとします。また電気双極子の電荷は+とーで同量であるとします。そうすると、上記のCoulombポテンシャルの距離成分はTaylor展開により簡略化され、
![]()
と言う形式で記載できます。
またこの問題はCartesian座標系で表すよりも、z軸からθだけ離れた角を持つ、つまり電場を球面座標で表す方がより明解な解答になりそうです。そこで、次の変換式(いわゆるJacobian)を使用して座標変換をしてあげます。eと言うのは、各座標系での単位ベクトルとなります。

ここの計算は偏微分を丁寧にやれば、なんとかなります(と言いつつ、答えが合っているかどうか途中自信がなくなることはありますよね・・・)。
そこで求めた結果が、

となります。したがって、この答えはθ方向に対してsin方向の電場を有することから、電場のカーブはsinθの特性となり、Powerで換算するとsinθの二乗、つまり八の字のカーブの特性になると言う具合です。
