みすてぃっく☆ばる～ん ark20解説

本記事はPCゲーム「みすてぃっく☆ばる～ん」のエディットで作ったステージの解説になります。みすてぃっく☆ばる～んのルール等については解説しませんので、未プレイの方はとりあえずみすてぃっく☆ばる～ん無印をステージ4くらいまでクリアしてからお読みください。

さて、今回解説するのは私の20作目となるこの作品です。

この作品は、難問奇問が跋扈するみすてぃっく☆ばる～んのエディットステージの中では易しいステージであり、考えられるパターンを総当たりして最悪を引いても20分といったところかと思います。できることの幅が狭く、強いミスリード要素もないため、はまってしまう人もあまりいないでしょう。自分で言うのもなんですが、みすてぃっく☆ばる～んのステージとしては、特筆するべきところもない凡作だと思います。

しかしながら、このステージは単なるみすてぃっく☆ばる～んのステージではありません。実はこのステージの裏側にはグラフ理論の定理が存在しているのです。

まず、早速ですが、この盤面をグラフに置き換えてみます。

盤面を見るとマジカルボールは全て三叉路に位置し、それ以外のところで道の分岐は発生していません(右下のボール周りはちょっと特異な形をしていますが、周囲3つのボールのいずれかを取ってから飛び込むしかないので、そのそれぞれと一方通行の道で結ばれていると見ることができます)。したがって、グラフの頂点(黒丸)をステージ中のボールに対応させ、通路でつながっているボール同士を辺で結ぶことでその構造をうまく表せそうです。

この考え方に基づいて実際にark20の盤面をグラフにすると下図のようになります。ちなみに作図はペンパくんです。

ここで頂点S1、S2はミスティアが初手で取りえる2つのボールに対応し、頂点Gはラストボール確定の右下のボールに対応しています。

ここでみすてぃっく☆ばる～んのルールを思い返してみると、このステージは、

1.　ミスティアの経路はS1、S2、Gも含め、20個全ての頂点を通る。

2.　どの辺も1回しか通れない。また、どの頂点からも3本しか辺が伸びていないので、どの頂点も1回しか通れない。

この条件を満たすような、S1またはS2からGまでの経路を見つけることが目的であるということになります。扉に対応する辺を通るなら鍵の辺を先に通らねばならない、実はS1-S2辺は通れない、という他の制約もありますが、まずは上記1.2.を満たす経路が見つからないことには話が始まりません。

1.2.の条件を満たすような、「ある頂点を出発し、全ての頂点を1回ずつ通ってどこかの頂点に着くような道」を、グラフ理論の言葉でハミルトン道と言います。

たとえば下図はこのグラフ上のハミルトン道となります。

また、同じように全ての頂点を1回ずつ通る経路で、ぐるっと一周するようなものをハミルトン閉路と言います。下図はこのグラフのハミルトン閉路の一例です。

ハミルトン道やハミルトン閉路はグラフの構造によって存在したりしなかったりします。また、ハミルトン道が存在するグラフでも、その端点を指定すると存在しない可能性もあります。

さて、ハミルトン閉路はグラフ理論においてかなり興味深い対象なので、ハミルトン閉路が存在するための条件や、逆にハミルトン閉路が存在するという条件からグラフの性質を制限するような定理が多く見つかっています。

そのうちの一つが、今回の主役となる以下の定理です。

式を見ただけでは意味がつかみにくいですが、実例を見ると割と分かりやすい定理です。以降では実例を見ていきましょう。

まず、平面グラフとは、平面上に辺の交差なく描くことのできるグラフを、平面に描いたもの(数学用語ではグラフの平面への埋め込み)のことです。下図は平面グラフの一例です。

平面グラフがあると、グラフの「面」が定義できます。辺で囲まれた領域一つ一つが面です。また、外側も一つの面としてみなします。上図のグラフは7つの面を持ちます。

面は、3つだけの頂点で囲まれているものも考えられますし、たくさんの頂点で囲まれているものもあり得ます。面fに対し、その周囲にある頂点の数を面の大きさと呼び、|f|で表すことにします。

Grinbergの定理では各面について|f|-2の値を考えますので、先の例について、各面に|f|-2の値を書き込んでみましょう。すると、

こうなります。さて、このグラフは下図のようなハミルトン閉路を持ちます。

ここでその内側にある数の和と外側にある数の和をそれぞれ計算すると、ともに8となり等しくなります。

もう一例試してみましょう。先ほどのグラフは下図のようなハミルトン閉路も持ちます。

確かにこの場合でも内外とも8で等しくなっています。

どんな平面グラフでも、どんなハミルトン閉路でも、この値は内外で等しくなる、というのがGrinbergの定理の主張するところです。

なお、グラフ理論の心得がある人であればこの定理を証明するのは易しく、ハミルトン閉路は元の平面グラフの平面双対を2つの木に分断すること、木の辺数が頂点数-1であることあたりを利用してハミルトン閉路の長さを内外両方から計算すると証明できます。そんな定理が1968年なの?と思う方もあるかと思いますが、グラフ理論含む離散数学は数学の中で歴史が浅い方なので、こういうこともあります。

さて、Grinbergの定理を知ったところで、いよいよこれを用いてark20の構造を見ていきましょう。ark20の構造を再掲します。説明のため、各面について|f|-2の値も書き込んでおきました。

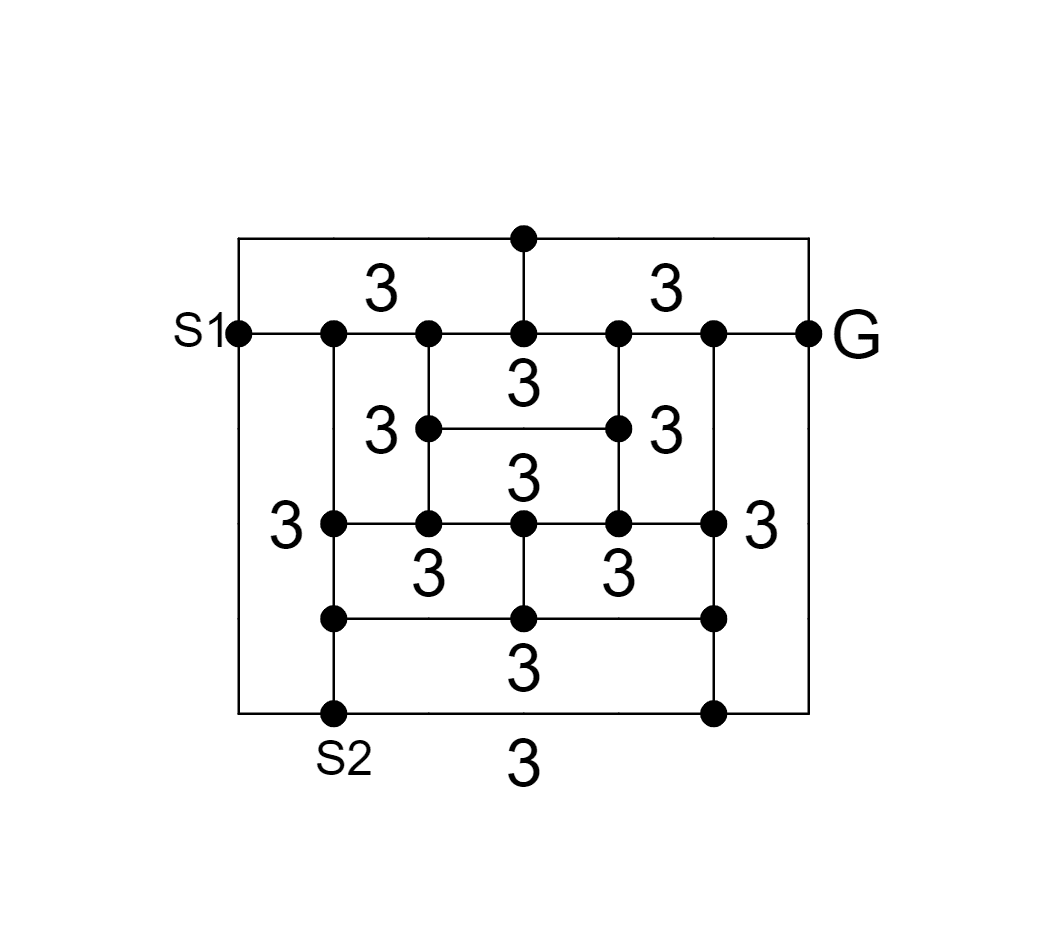
ずらりと3が並んでいますね。このグラフは正十二面体グラフと呼ばれるもので、その名の通り正十二面体の頂点・辺・面のつながりを表したものとなっています。そのため面は12個、その全てが大きさ5なので、|f|-2を書き込むと3が並ぶことになります。

さて、ark20で見つけたいものはS1またはS2からGへのハミルトン道でした。一方でGrinbergの定理はハミルトン閉路に関するものなので、少しだけ状況が違います。ではどうするかというと、

こうします。S1からGへのハミルトン道を考えるなら、元のグラフにS1とGを結ぶ辺を加えて、新しいグラフを作るのです。このグラフは元のグラフの面を1つ割っているので13個の面を持ちます。もし元のグラフがS1からGへのハミルトン道を持っているなら、新しいグラフはS1-G辺を継ぎ足して、S1-G辺を含むハミルトン閉路を持つことになります。

ところが、それが存在するとおかしなことが起こることに気付きます。もし辺を加えた後のグラフがS1-G辺を含むハミルトン閉路を持つならば、それについてGrinbergの定理が成立しているはずです。しかしこのハミルトン閉路はS1-G辺を含むので、1と書かれた面と2と書かれた面とは内外に分断されることが確定しています。これではGrinbergの定理の等号を満たすことができません。他の面をどう割り振っても、内外で3での剰余が合わないためです。

すると背理法的に、元のグラフはS1からGへのハミルトン道を持たないということが言えます。

同様に考えると、S2からGへのハミルトン道も存在しません。

はて、困ってしまいました。当初の目的を満たす道筋は存在しないということになってしまったのです。しかし、解無しステージが投稿されているわけではもちろんありません。

実はark20は、ハミルトン道を見つけるステージではないのです。投稿されたステージをよーく見ると、1か所だけ、条件1.2.が破れている場所、2回通れる辺があります。

そうです。扉がある辺です。

ハミルトン道は存在しないのですから、この辺を0回または1回通るような解は存在しません。隣接する頂点はともに三叉路なので、通れるのは2回までです。ということで、扉のある場所を2回通ることが確定します。みすてぃっく☆ばる～んの問題としてみると、ここが唯一引っ掛かりえるところですかね。扉の辺を他の辺同様1回しか通れないものと思い込んでしまうと正解に至れません。

この時点では扉の向こうのボールを取ってすぐ折り返すのか、ひと手間くるっと回って帰ってくるのかまではわかりません。しかし鍵を取ることは確定しますし、扉の周囲の牢屋がちょっと閉まっただけで2回通過ができなくなってしまうので、大幅にパターンが削れます。破綻無く鍵まで辿り着けるパターンが数パターンなので、このことを知って挑んだなら、最悪を引いてもせいぜい5分でしょう。

このように、このステージの裏にはグラフ理論の定理が潜んでいるのでした。実際のところは、こんなこと考えるよりミスティアを手あたり次第動かした方が早く解けますけれどね。

この例を見るとGrinbergの定理は強力に見えますが、これを根拠にハミルトン閉路が存在しないことを示せるのは、対象がかなり特殊なグラフである場合に限られます。

ark20に対応するグラフはほぼ全ての面について大きさが5で揃っていたので内外でΣ(|f|-2)の値が合わないことが言えましたが、面の大きさがまちまちなグラフでは大抵の場合うまく割り振れば数を合わせることができるため、ハミルトン閉路の存在を否定できません。

では今回のように多くの面について大きさを揃える方向で他に問題が作れないかと考えると、

・大きさを3で揃えると、各面に割り振られる数は1となり、全くといっていいほど意味がありません。

・大きさを4で揃えると、各面に割り振られる数は2。ark20と同じような理論で問題を作ることはできますが、|f|をほとんど4で揃えるということはグラフがほぼ二部グラフになるということであり、ボールを白黒に塗り分けて…というパリティの考え方で事が済みます。Grinbergの定理を持ち出す必要がないのですね。

・大きさを5で揃えたのがark20です。

・大きさを6以上で揃えることは(ほぼ)できません。全ての頂点から3本の辺が伸びているような(グラフ理論の言葉で3-正則という)平面グラフについて、Σ(|f|-6)の値を求めると必ず-12になるという定理があるためです。この定理ゆえ、3-正則な平面グラフは必ず大きさ5以下となる面をそれなりに含まざるをえず、そんなにずれた面があっては、Grinbergの定理の出番はありません。かといって頂点から伸びる辺の数を4以上に増やすとその頂点を2回以上通れるようになり、根本が破綻してしまいます(一応、みすてぃっく☆ばる～んのパーツをうまく組み合わせれば「1回しか通れない四叉路」を作ることは可能ですが、スペースを食います)。

というわけで、ark20はこの定理が活きる数少ない盤面なのでした。

ただし、他の問題が全く作れないかというとそんなことはありません。今回、Grinbergの定理を使って閉路の内外で|f|-2の和が合わないことを示したとき、その根拠は「3での剰余が合わない」でした。3での剰余を考えるのであれば、面に書かれた数字に3と6が入り混じっていても同じことです。つまり、五角形と八角形ばかりで盤面を作れば、全く同じ論理が通用することになります。3-正則平面グラフがΣ(|f|-6)=-12を満たさねばならないことに注意すると、五角形14個と八角形1個からなる盤面や、五角形16個と八角形2個からなる盤面は成立する可能性があるといえますね。ark20はまだ多少スペースに余裕があるので、このくらいの拡大はできると思います。もっとも、その程度の拡大をしたところで劇的に難度が上がるわけでも新しい発見があるわけでもないので微妙ではありますが。

また、みすてぃっく☆ばる～んにおいては容易に通路を一方通行にすることができます。これとグラフの有向閉路に関する他の定理を併用すると、より複雑な「悪いこと」ができる可能性がある、ということにark20投稿後に気付きました。

これについては、そのうちまた投稿するかもしれません。まだ机上の段階なので、実らず諦めるかもしれません。もし首尾よく完成したとして…一筆書き系の問題ばかり投稿しても正統派の問題も作れと言われそうなので、しばらく間を開けて、ark40とかですかね。

それではしばらくの後、再び牢屋とマジカルボールだらけのステージでお会いしましょう。完成するといいな!