
等角写像
複素関数$${w=f\left( z \right)}$$は、$${z=x+iy\in \mathbb{C}}$$ から$${w=u+iv\in \mathbb{C}}$$への対応を与えるものだが
図で示そうとすると2次元ベクトル$${\left( x,y \right)}$$から2次元ベクトル $${\left( u,v \right)}$$ への対応を表現することになり、俯瞰するには4次元空間が必用である。
そこで、$${\left( x,y \right)\to u=\operatorname{Re}f}$$
と$${\left( x,y \right)\to v=\operatorname{Im}f}$$
という2つの対応の図を考える。
(1)$${w=\frac{1}{z}}$$の場合、
$${u=\operatorname{Re}\frac{1}{z}}$$ ,$${v=\operatorname{Im}\frac{1}{z}}$$と書いて
$${u+iv=\frac{1}{x+iy}=\frac{x-iy}{{{x}^{2}}+{{y}^{2}}}}$$ より
$${\left( x,y \right)\to \left( \frac{x}{{{x}^{2}}+{{y}^{2}}},\frac{-y}{{{x}^{2}}+{{y}^{2}}} \right)}$$
すなわち、
$${\operatorname{Re}\frac{1}{z}=\frac{x}{{{x}^{2}}+{{y}^{2}}}}$$, $${\operatorname{Im}\frac{1}{z}=\frac{-y}{{{x}^{2}}+{{y}^{2}}}}$$となる。
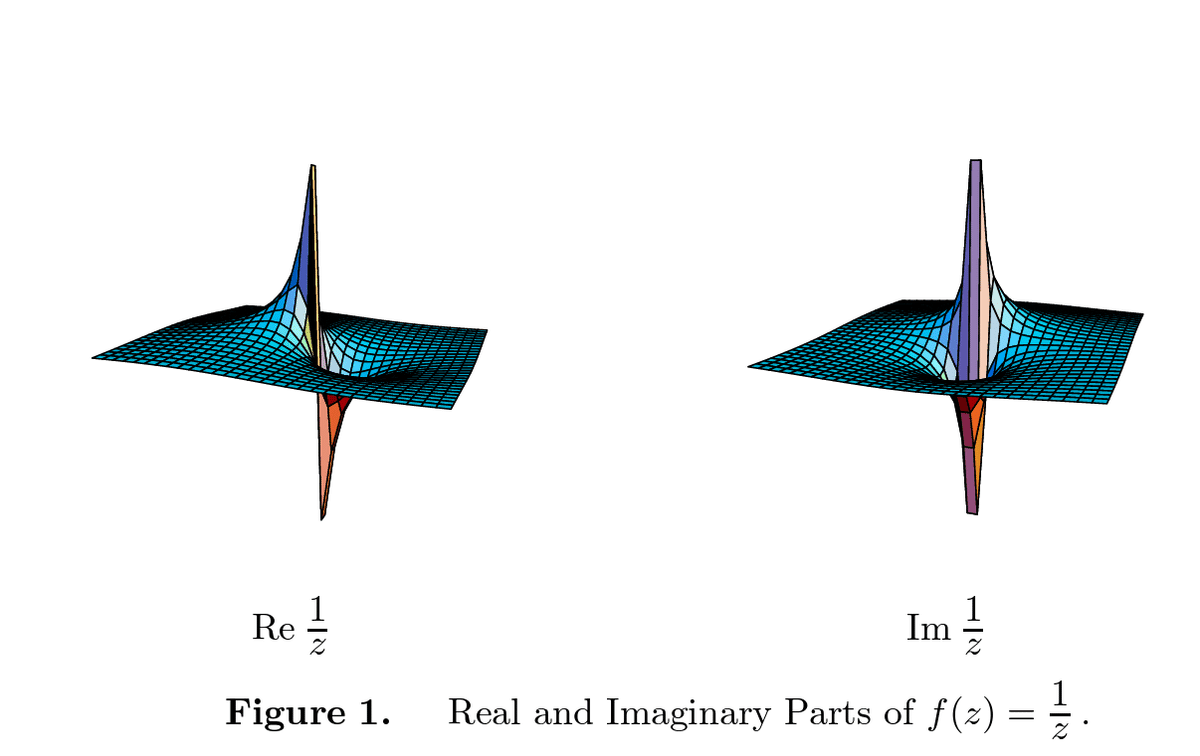
図1を見ると$${z=0}$$ では$${w=\infty }$$が対応していることがわかる。この場合複素数の$${\infty }$$というのは実数の$${+\infty }$$とは違い符号がなく上にも下にも限りなく遠い。
(2)$${w={{e}^{z}}}$$の場合
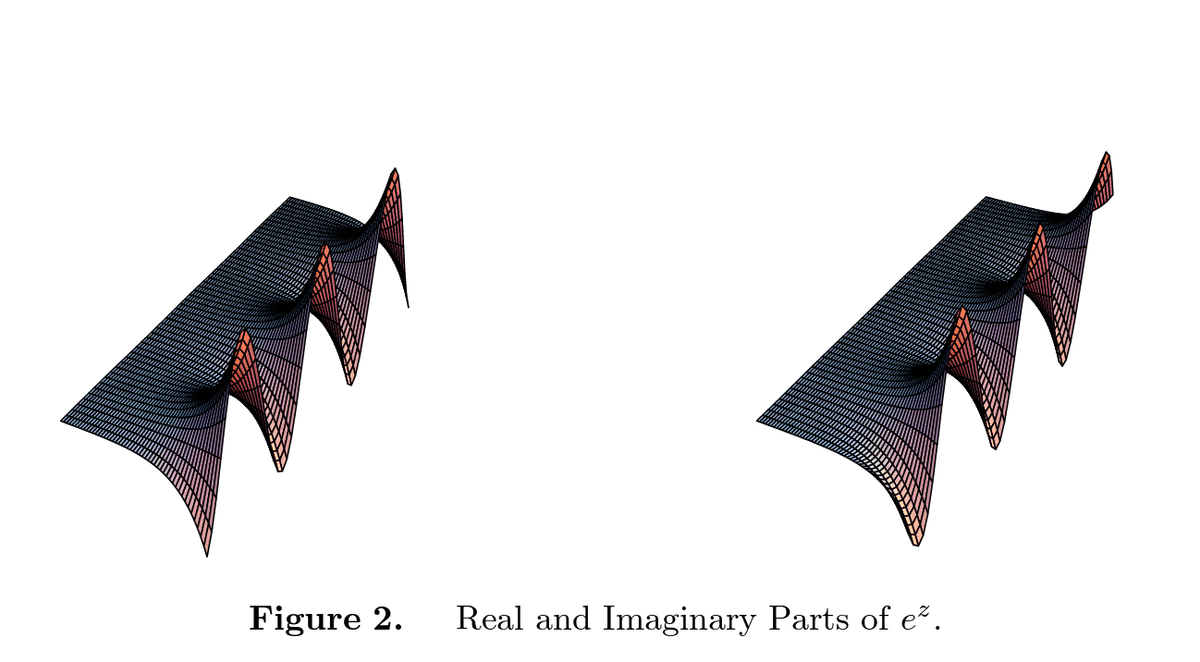
オイラーの公式を使って
$${{{e}^{z}}={{e}^{x}}\cos y+{{e}^{x}}\sin y}$$
となり、左図が$${\operatorname{Re}{{e}^{z}}}$$、右図が$${\operatorname{Im}{{e}^{z}}}$$ をあらわす。左には$${\cos y}$$ 右には$${\sin y}$$という周期関数がみえている。
(3)$${w=\log z}$$
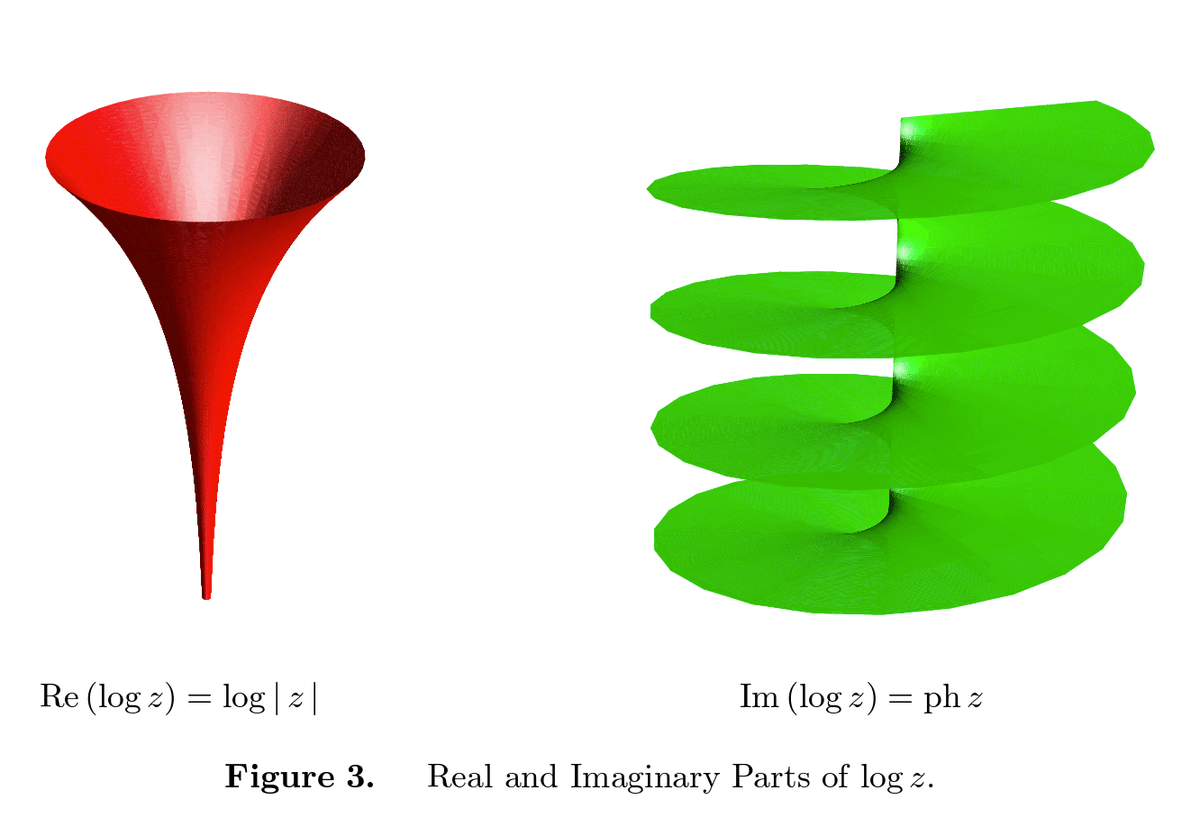
$${u=\operatorname{Re}\left( log\,z \right)=\log \left| z \right|}$$ はラッパのようなかたち, $${v=\operatorname{Im}\left( \log z \right)=\arg z}$$は$${2\pi }$$ の整数倍の繰り返しで螺旋状に上にも下にも伸びる無限階段(車のパーキングランプ)になる。
(4)$${w=\sqrt{z}}$$
この場合$${z=r{{e}^{i\theta }}}$$ と極座標を用いると、
$${\sqrt{z}=\sqrt{r{{e}^{i\theta }}}=\sqrt{r}{{e}^{i\theta /2}}=\sqrt{r}\left( \cos \frac{\theta }{2}+i\sin \frac{\theta }{2} \right)}$$
となり、$${\arg z}$$が$${2\pi }$$ 増加しても$${\sqrt{z}}$$ では$${\pi }$$ しか増えない、その結果 $${-\sqrt{z}}$$ に到達する。さらに$${2\pi}$$増加してはじめて$${\sqrt{z}}$$にもどる。というわけで実数部分と虚数部分では上下逆にしたような、2重らせんが左図、右図で向かい合う。

歴史的に見て、流体の考察はD.ベルヌイ(1700-1782)やL.オイラー(1707-1783)などによる非圧縮性完全流体の数学的解析から始まった。
流れが平面内に限られる2次元問題では、$${t}$$ を時間のパラメータとして、非圧縮、渦なし流体の場合
流速$${U=\left( u\left( x,y,t \right),v\left( x,y,t \right) \right)}$$ は
$${divU=\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0}$$
$${rotU=\frac{\partial u}{\partial y}-\frac{\partial v}{\partial x}=0}$$
をみたす。定常流では$${u\left( x,y,t \right)}$$は時間$${t}$$に依存せず単に$${u\left( x,y \right)}$$と書いて構わない。一般に$${divU>0}$$なら流体は膨張し密度は減少する。$${divU<0}$$なら流体は圧縮され密度は増加する。そして、$${divU=0}$$となるとき速度場は非圧縮であるという。また、$${rotU}$$は回転をあらわし、$${rotU=0}$$は渦ができないという条件である。そしてまた、これは複素関数論におけるコーシーリーマンの方程式でもある。つまり、$${W\left( x,y,t \right)=u\left( x,y,t \right)+iv\left( x,y,t \right)}$$ は$${z=x+iy}$$の正則関数となる。したがって、$${u,v}$$は$${\left( x,y \right)}$$の関数としてたがいに共役な調和関数である。多くの場合、調和関数には共役な調和関数が存在するが、面白いことに、その存在、非存在は領域が単連結かどうか、つまり領域に穴あいているかあいていないかというトポロジー的性質に依存するのである。たとえば上の例で、対数ポテンシャル$${u\left( x,y \right)=\log r=\frac{1}{2}\log \left( {{x}^{2}}+{{y}^{2}} \right)}$$は原点をのぞいた$${\mathbb{C}\backslash \left\{ 0 \right\}}$$という領域で定義され原点にあなを持ち、$${\log z}$$という多価関数の実数部になっている。そして$${\log z}$$ の虚部$${\arg z}$$ は $${\mathbb{C}\backslash \left\{ 0 \right\}}$$全体で連続となるようにはできない。$${w=\frac{1}{z}}$$の場合は定義域は$${\mathbb{C}\backslash \left\{ 0 \right\}}$$という単連結でないひとつ穴であり$${u\left( x,y \right)=\frac{x}{{{x}^{2}}+{{y}^{2}}}}$$,$${v\left( x,y \right)=-\frac{y}{{{x}^{2}}+{{y}^{2}}}}$$は原点以外ではコーシーリーマンはみたすが、原点は特異点となる。
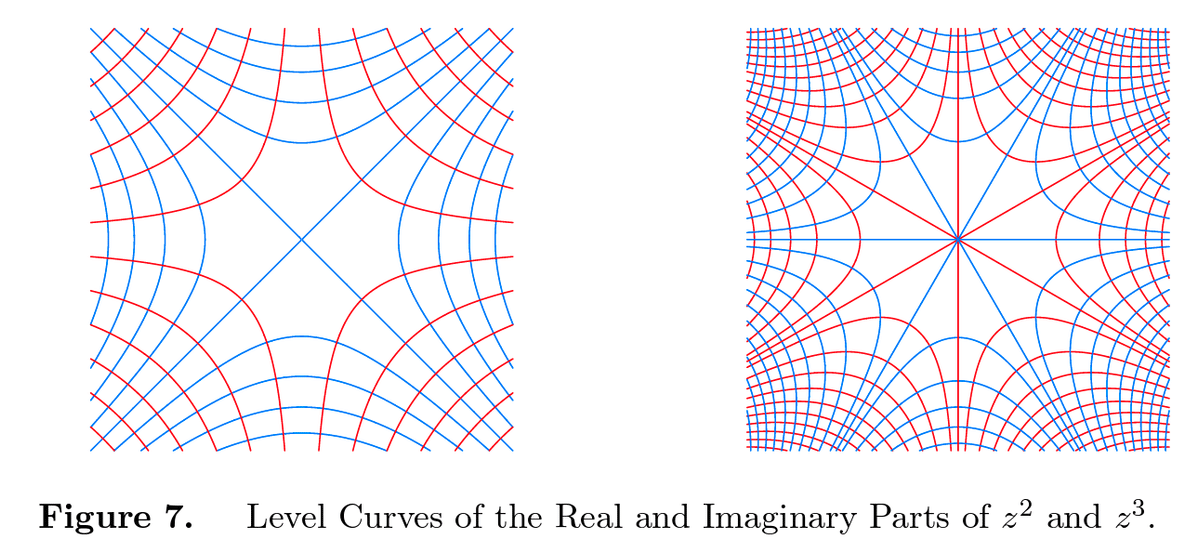
(5)$${w=f\left( z \right)={{z}^{2}}}$$
すなわち、$${u={{x}^{2}}-{{y}^{2}}}$$,$${v=2xy}$$は$${\mathbb{C}}$$ 全体で正則であるが1対1でない。逆関数$${z=\pm \sqrt{w}}$$ は原点以外で多価(2価)である。さらに$${f'\left( z \right)=2z}$$で$${z=0}$$ で$${f'\left( z \right)=0}$$ となっていることから等角性をみたしていない。しかし、全平面で考えるのではなく、局所的に単連結となるような領域にかぎって考えるときには、$${f'\left( z \right)\ne 0}$$であり等角写像となり1対1とできる(分枝を持つ)。絶対値の大きさは$${\left| w \right|={{\left| z \right|}^{2}}}$$となり、角度は$${\arg w=\arg {{z}^{2}}=2\arg z}$$ と2倍になる。したがって、たとえば円の上右4分quadrant $${Q=\left\{ x>0,y>0 \right\}}$$は円上半分$${U=f\left( Q \right)=\left\{ \operatorname{Im}w>0 \right\}}$$ に移り、円の上半分は$${\left( -1,0 \right)}$$ に割れ目のある円
$${f\left( U \right)=\left\{ \left| w \right|<1,-\frac{\pi }{2}<\arg w<\frac{\pi }{2} \right\}}$$ に移る。四角は底辺が線分で左右辺が円周の一部でつくる3角形アイロンになる。
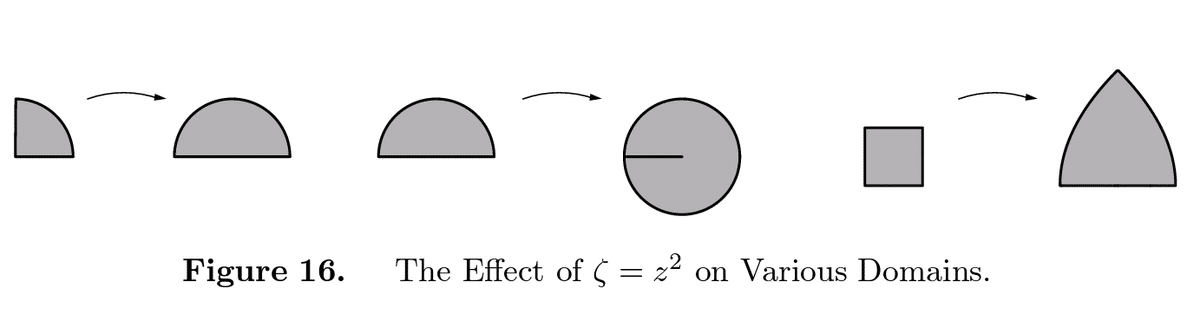
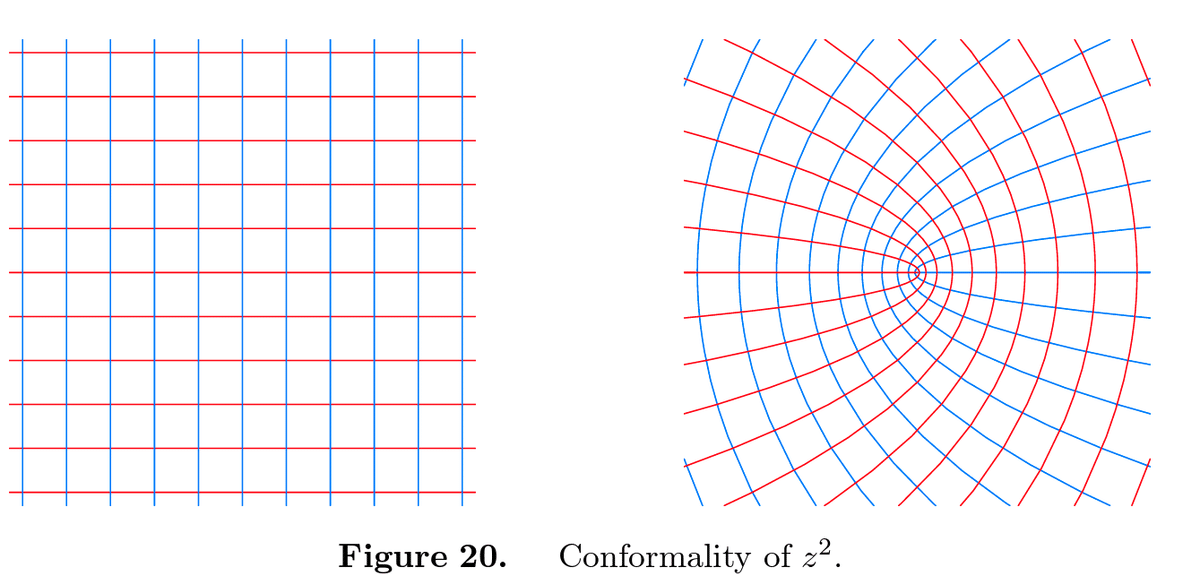
図20は$${{{z}^{2}}}$$ の等角性を示している。左図では$${x}$$ 軸$${y}$$ 軸が格子状(直交)に並んでいるのに対して、右図では$${u={{x}^{2}}-{{y}^{2}}=const}$$の曲線群と$${v=2xy=const}$$という等高線っでつくる曲線群が原点を除き直交しているのが見て取れる。90°を90°に移すというように角度が保存されている。
(6)$${w=\frac{1}{2}\left( z+\frac{1}{z} \right)}$$
興味深い例として、Joukowski写像がある。
実部の等高線(等ポテンシャル線)と虚部の等高線(流線)およびそれらを重ねたものは次図のようになる。

ロシアの飛翔物体研究者Joukowski(=NikolaiZhukovskii)が飛行機の翼の周りの定常流を研究するのにもちいた。
$${\frac{dw}{dz}=\frac{1}{2}\left( 1-\frac{1}{{{z}^{2}}} \right)=0}$$$${\Leftrightarrow \pm }$$$${z=\pm 1}$$
より定義できない$${z=0}$$のほかに等角性が崩れる点$${z=\pm 1}$$ がある。それ以外では等角写像になっている。
$${z={{e}^{i\theta }}}$$のとき$${w=\frac{1}{2}\left( {{e}^{i\theta }}+{{e}^{-i\theta }} \right)=\cos \theta }$$
となることより単位円をJoukovski写像で写すと実数線分$${\left[ -1,1 \right]}$$に写像される。円周でかこまれた面が線分に移るという意味で退化してしまっている。そして円のそとは$${w}$$平面を覆いつくし、単位円のなかも同様に$${w}$$平面を覆いつくす。実際逆関数をみれば$${z=w\pm \sqrt{{{w}^{2}}-1}}$$ であり、$${w=\pm 1}$$を除いてすべての$${w}$$は2つの異なる$${z}$$ から移されてくる。つまり、$${z=w\pm \sqrt{{{w}^{2}}-1}}$$は単位円の外$${\left\{ \left| z \right|>1 \right\}}$$ は線分以外$${\mathbb{C}\backslash \left[ -1,1 \right]}$$に移される。

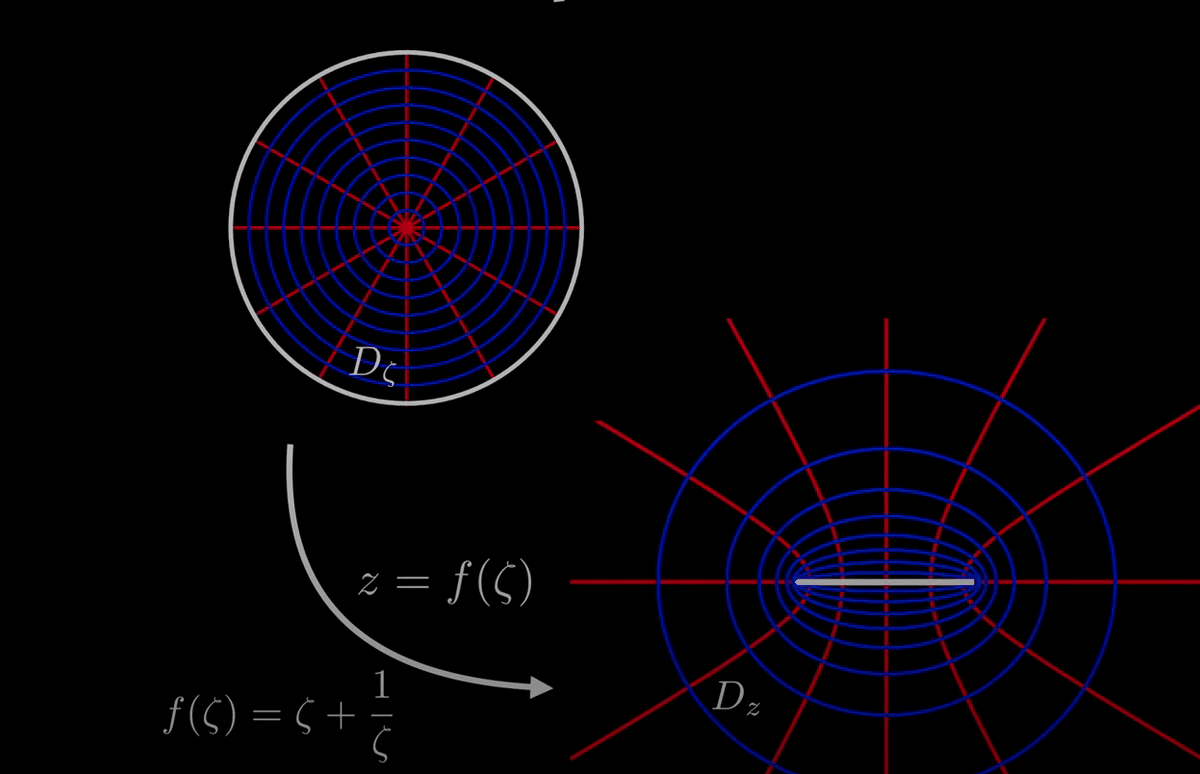
下の図22では中心Center と半径radusを色々変えてJoukovski写像で写したいくつかの結果を表している。右のほうにカスプと呼ばれるとがった点が現れるのは等角性の崩れる部分で飛行機の翼によく似ている。

等角写像の合成は再び等角写像となる。正則な関数$${w=f\left( x \right)}$$と正則な関数$${\zeta =g\left( w \right)}$$の合成はまた正則関数であることの証明は微積分学における合成関数の微分可能性をしめすこととおなじ。そして、$${\frac{d}{dz}g\circ f\left( z \right)=g'\left( f\left( z \right) \right)f'\left( z \right)}$$ において
$${g'\left( f\left( z \right) \right)f'\left( z \right)\ne 0}$$$${\Leftrightarrow }$$$${g'\left( f\left( z \right) \right)\ne 0}$$かつ$${f'\left( z \right)\ne 0}$$
を見ればわかるだろう。
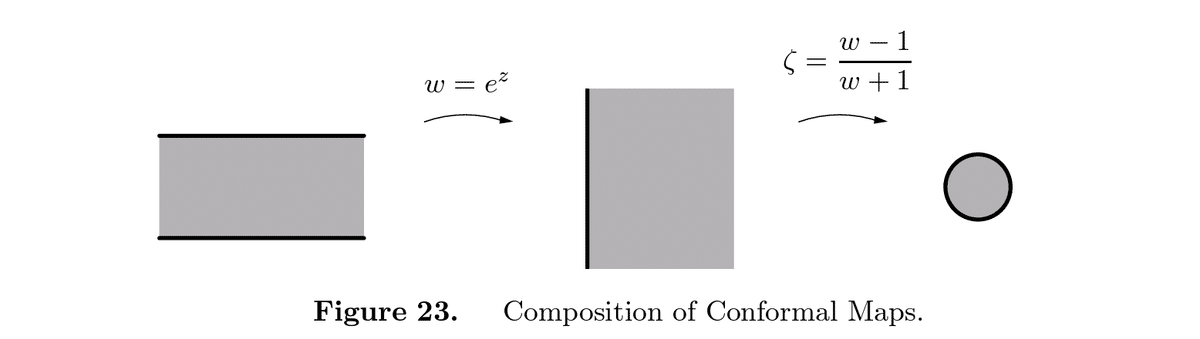
(7)$${\zeta =\frac{{{e}^{z}}-1}{{{e}^{z}}+1}}$$
上の図23は$${w={{e}^{z}}}$$ と$${\zeta =\frac{w-1}{w+1}}$$の合成を表している。
$${w={{e}^{z}}}$$は水平の帯
horizontal strip $${S=\left\{ -\frac{1}{2}\pi <\operatorname{Im}z<\frac{1}{2}\pi \right\}}$$を右半平面$${R=\left\{ \operatorname{Re}w>0 \right\}}$$に等角に写像する。他方$${\zeta =\frac{w-1}{w+1}}$$は右半平面$${R}$$を単位円$${D=\left\{ \left| \zeta \right|<1 \right\}}$$ に等角に写像する。その結果合成された関数$${\zeta =\frac{{{e}^{z}}-1}{{{e}^{z}}+1}}$$は$${S}$$ から$${D}$$ への等角写像となる。

(8) Riemann Mapping therem に続く
https://www.researchgate.net/publication/263058976_Riemann_Mapping_Theorem_by_Steepest_Descent
Riemann Mapping Theorem by Steepest Descent
March 2007
DOI:10.1080/00029890.2007.11920411
Authors:
この記事が気に入ったらサポートをしてみませんか?
