ブラウアーの不動点定理　

ブラウアーの不動点定理　
 
 円盤と円周はトポロジー的に異なる。
円盤は連続変換で１点に収縮できるが、円周はできない。これを基本群で表すと、$${{{\pi }_{1}}\left( {{D}^{2}} \right)=0}$$であり、$${{{\pi }_{1}}\left( \partial {{D}^{2}} \right)=\mathbb{Z}}$$という違いとなる。
 
Brouwer’s fixed point theorem
円盤$${{{D}^{2}}=\left\{ \left( x,y \right):{{x}^{2}}+{{y}^{2}}\le 1 \right\}}$$上で定義された連続関数を
$${F:{{D}^{2}}\to {{D}^{2}}}$$ とするとき、
$${F\left( x \right)=x}$$ となる$${x\in {{D}^{2}}}$$ 、すなわち不動点が存在する。
 
証明）背理法を使う。$${\forall x\in {{D}^{2}}}$$ で$${F\left( x \right)\ne x}$$を仮定する。
$${G:{{D}^{2}}\to \partial {{D}^{2}}}$$
を以下の図のように定義する。

F(x)とｘを結びその延長線が円周にぶつかった点をG(x)とする

（$${F\left( x \right)=x}$$のときはそのような$${G}$$ が定義できない！）
 いま、次の１，２を正しいとして証明をおわり、そのあとで1を検討する。
 
１．$${G}$$ は連続
２．$${x\in \partial {{D}^{2}}}$$ のとき、$${G\left( x \right)=x}$$ （これは図をみれば明らかだろう）
 包含写像を
$${i:\partial {{D}^{2}}\to {{D}^{2}}}$$
とおくと、$${\forall x\in \partial {{D}^{2}}}$$ に対して、
$${\left( G\circ i \right)\left( x \right)=G\left( i\left( x \right) \right)=G\left( x \right)=x}$$
となる。つまり、$${G\circ i=i{{d}_{\partial {{D}^{2}}}}}$$
となる。

連続写像の可換図は基本群の可換図を引き起こす

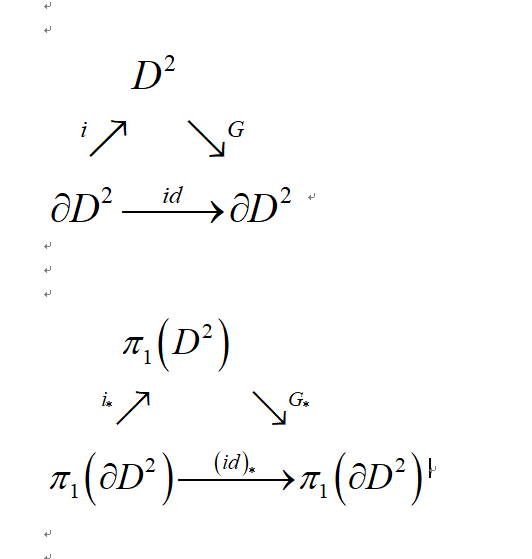
$${{{\pi }_{1}}\left( \partial {{D}^{2}} \right)}$$からそれ自身への恒等写像が$${{{\pi }_{1}}\left( {{D}^{2}} \right)}$$ という自明群を間に挟んだ準同型の合成$${{{G}_{*}}\circ {{i}_{*}}}$$ としてあらわされるというこの可換図式は不合理なものである。
 つまり$${{\gamma \in{\pi }_{1}}\left( \partial {{D}^{2}} \right)}$$のとき
$${\left( {{G}_{*}}\circ {{i}_{*}} \right)\left( \gamma \right)=0}$$
他方、 $${G\circ i=i{{d}_{\partial {{D}^{2}}}}}$$
より$${{{\left( G\circ i \right)}_{*}}\left( \gamma \right)=\gamma }$$
これは、$${{{\left( G\circ i \right)}_{*}}={{G}_{*}}\circ {{i}_{*}}}$$
を考えると矛盾をきたしている。
証明終わり。
 
 
証明中用いた事実$${{{\left( G\circ i \right)}_{*}}\left( \gamma \right)=\gamma }$$と$${{{\left( G\circ i \right)}_{*}}={{G}_{*}}\circ {{i}_{*}}}$$の部分は
次の事柄を使っている
 定義：
$${\left( A,a \right)}$$ と$${\left( B,b \right)}$$を位相対とする。基本群の準同型写像
$${\varphi :A\to B}$$
なる連続写像が、$${\varphi \left( a \right)=b}$$をみたすとき、
$${\varphi :\left( A,a \right)\to \left( B,b \right)}$$
とかく。
$${\gamma :\left[ 0,1 \right]\to A}$$なる曲線が$${\gamma \in {{\pi }_{1}}\left( A,a \right)}$$であるとき、ループの連続写像はループであり、ホモトピーの連続写像もホモトピーであるから
$${\varphi \circ \gamma :\left[ 0,1 \right]\to \left( B,b \right)}$$ は、
$${\varphi \circ \gamma \in {{\pi }_{1}}\left( B,b \right)}$$とみなせる。この変換を
$${{{\varphi }_{*}}:{{\pi }_{1}}\left( A,a \right)\to {{\pi }_{1}}\left( B,b \right)}$$ とかく。
このとき$${{{\varphi }_{*}}}$$ は次の性質を持つ。
（１）$${{{\left( id \right)}_{*}}=id}$$
（２） $${\varphi :\left( A,a \right)\to \left( B,b \right)}$$,$${\psi :\left( B,b \right)\to \left( C,c \right)}$$があるとき、$${{{\left( \psi \circ \varphi \right)}_{*}}={{\psi }_{*}}\circ {{\varphi }_{*}}}$$
 
 
１．について。
$${G}$$ が連続写像であることの証明
$${j:{{D}^{2}}\to {{D}^{2}}\times {{D}^{2}}\backslash \left\{ \left( x,x \right):x\in {{D}^{2}} \right\}}$$
$${j\left( x \right)=\left( x,F\left( x \right) \right)}$$とおくと
$${F}$$の連続性より$${j}$$は連続写像である。
$${H:{{D}^{2}}\times {{D}^{2}}\backslash \left\{ \left( x,x \right):x\in {{D}^{2}} \right\}\to \partial {{D}^{2}}}$$
を下の図できめる。

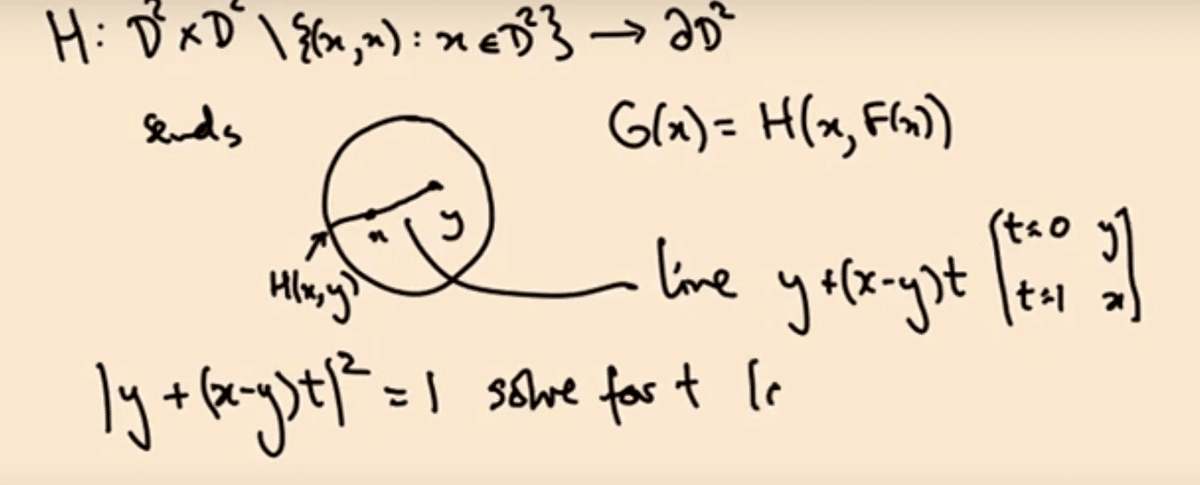
$${y}$$ と$${x}$$ を結ぶ直線$${x+\left( x-y \right)t}$$ ,$${t\in \left[ 0,1 \right]}$$ が円周に交わる点が$${H\left( x,y \right)}$$ である。つまり、$${{{\left| x+\left( x-y \right)t \right|}^{2}}=1}$$より、この２次方程式の解$${t=t\left( x,y \right)}$$ を求めると
$${t=\frac{-y\cdot \left( x-y \right)+\sqrt{{{\left( y\cdot \left( x-y \right) \right)}^{2}}+{{\left| x-y \right|}^{2}}\left( 1-{{\left| y \right|}^{2}} \right)}}{{{\left| x-y \right|}^{2}}}}$$
となるので、$${H\left( x,y \right)=x+\left( x-y \right)t\left( x,y \right)}$$の連続性がわかる。
 
$${G\left( x \right)=H\left( x,F\left( x \right) \right)}$$
とかけるので、連続写像$${j}$$ と連続写像$${H}$$の合成として、$${G}$$ が連続写像となることの証明はおわる。