４．情報源の符号化

符号化

あるアルファベットに属するシンボル系列から別のアルファベットに属するシンボル系列への写像を符号、変換操作を符号化という。

また、符号化により得られる系列を符号語という。

情報工学では、符号アルファベット$${X}$$にて、$${X}$$に属する符号シンボル$${\{0,1\}}$$の2元符号を扱う。

平均符号長

情報を符号化して、伝送する。
この際に、符号シンボルの総数を減らしたい。

符号長の平均（平均符号長$${L}$$）を小さくすることを考える。

情報シンボル$${s_1,s_2, \cdot\cdot\cdot s_j}$$を符号シンボル$${\bold x}$$の系列で符号化。

$${L=\displaystyle \sum_{j=1}^J P(s_j)lj}$$

以下の平均符号長を考える。

$${L_A=0.1\times2+0.2\times 2=0.6}$$
$${L_B=0.1\times1+0.2\times 2=0.5}$$

$${L_A \gt L_B }$$より、$${L_A}$$の方が効率的。

効率・冗長度

r元符号化における平均符号長$${L}$$の下限は、エントロピーに等しいから、

$${\eta=\displaystyle\frac{H_r(S)}{L}\leq1}$$

$${\eta}$$は、$${L}$$が短いほど1に近づき高効率。

ハフマン符号化

ハフマン符号は、文字列をはじめとするデータの可逆圧縮する方法。

試験では、平均符号長さが最小となる符号を作成することが問われる。

前提として、コンピュータの世界は"0","1"である。
（だから、情報理論のlogの底は2）
A～Zまでを"0","1"だけで表現する。

一意に復号可能/不可能

サイズを小さくする行為は、扱う数字の数を少なくする。
a~dを次のように割り当てれば、最小の個数で符号化できる。

• a→0

• b→1

• c→00

• d→10

• e→01

• f→11

以降、3個、４個で並べることができる。
確かに"0"/"1"、少なく表現できているが、問題点がある。

"011001"を復号（英字に直す）せよ。

１つ目は、0だからaかな？
しかし、次の1を考えるとeかな？

要するに、先ほどの割り当てでは復号ができない。
これを一意復号不可能という。

一意復号可能になるように割り当ててみる。(わかりやすくa~dまでにする)

• a→0

• b→01

• c→011

• d→0111

これは、0のあとに1が何個続くか（１で区切る）によって、復号する。

"011001"を復号（英字に直す）せよ。

1つ目は"0"で、"1"が２つ続くから、c。
"0"が２つ並ぶと、b~dはない。つまり、初めの"0"はa。
残りは"01"だから、b。
したがって、"cab"

これで、先ほど解けなかった問題ができるようになった。

瞬時復号

先ほどよりも決定的に復号する一意復号の方法が、
瞬時復号（一意復号の１つ）。

一意復号した時に、"0"が２つ並ぶと、b~dはないとなった。
これは、前方の"0"で、”a"or"b,c,d"。
次を確認しないと未確定な状態である。

次の"0"と"1"。合計３つを確認して初めの"0"の復号が確定した。

後続する符号を参照せずに復号可能になる場合を瞬時復号可能という。
視覚的に割り当てるには、木を作成する。

1. １つの節点から"0","1"を出して、一方を割り当てる。（例では"0"）

2. もう一方（例では"1"）の節点から"0","1"を出して、
   先ほどと同じシンボルを選ぶ。（例では"0"）

3. 最後の節点から"0","1"を出して両方を割り当てる。

• a→0

• b→10

• c→110

• d→111

"011001"を復号（英字に直す）せよ。

"0"はa。
"0"の前に"1"が２つはc。
※最後の"１"は問題が悪い。

前後関係を検討する前には、復号されている。
これが瞬時復号可能である。

因みにa~zを瞬時復号可能になるように符号化すると、

• a→0

• b→10

• c→110

• x→11…0 ("1"が連続23個)

• ｙ→11…0 ("1"が連続24個)

• z→11…1 ("1"が連続25個)

平均符号長を求める

符号a,b,c,dの確率は、それぞれ0.5,0,2,0.1,0.2のとき、
ハフマン符号化した場合の平均符号長を求めよ。

初めに、確率の大きい順に並べ替える。（a>b=d>c）
次に、確率の小さい同士で枝から節点を得る。
最後まで繰り返す。

確率が大きいということは出現しやすいことを意味している。
だから、aが文字数1つであることは妥当。

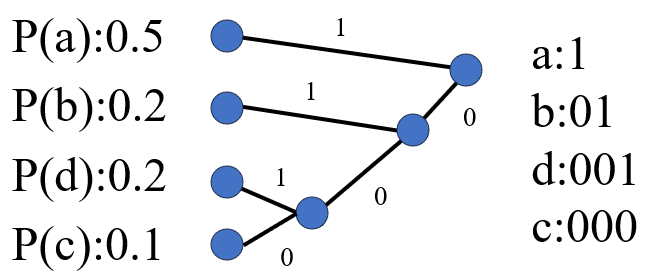
平均符号長$${L}$$は、

$${L=1 \times0.5+2 \times0.2+3 \times0.2+3 \times0.1=1.8}$$

コンパクト符号化

情報源$${S}$$の符号化で、一意に復号可能な符号の中で効率が最大。
平均符号長が最小になる符号をコンパクト符号化という。

情報源シンボル$${s_j}$$に対応する復号語長$${l_j}$$として、
$${\log \displaystyle \frac{1}{P(s_j)}=l_j}$$

$${\log \displaystyle \frac{1}{P(s_j)}}$$は、整数である。

情報源符号化定理

コンパクト符号化にて、整数の場合のr元符号の生成を考えたが、整数限定である。

整数以外でも考える。

$${\log \displaystyle \frac{1}{P(s_j)} \leq  l_j \lt \log \displaystyle \frac{1}{P(s_j)}+1}$$

$${P(s_j)}$$をかけて、$${j}$$の総和を取る。
$${H_r(S) \leq L \lt H_r(S)+1}$$

この式を$${n}$$次拡大すると、
$${H_r(S^n) \leq L^{(n)} \lt H_r(S^n) +1}$$
$${nH_r(S) \leq L^{(n)} \lt nH_r(S) +1}$$
$${H_r(S^n) \leq \displaystyle\frac{L^{(n)}}{n} \lt H_r(S^n) +\frac{1}{n}}$$

極限値を考えると、
$${\displaystyle \lim_{ n \to \infty }\displaystyle\frac{L^{(n)}}{n} = H_r(S)}$$

この極限値は、情報源シンボル(記号)あたりの平均符号長がエントロピーに収束していることを示している。