いろいろな関数

クロネッカーのデルタ

ディラックのデルタ関数

以下の３つの性質を有する。

入力値が０でないなら出力値も０
入力値が０なら出力値は無限

x=0地点における集中荷重、衝撃力、点電荷、点熱源を表現する。

積分したら１

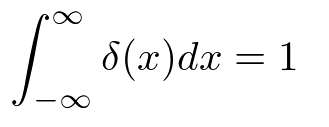
ある関数f(x)との積の総和はf(0)

積分するとヘヴィサイドステップ関数

$$
\int_{-\infty}^{t}\sigma (x)dx = h(t)
$$

デルタ関数の入力値ずらす

入力値０に限らず、任意の入力値ξに対するデルタ関数。
δにはあいかわらず０が入る。

任意の点x=ξにおける集中作用
ξは作用が与えられる点(source point)
xは区間内の任意の点(observation point)

$$
\delta(x-t)=\begin{cases} \infty & (x=t) \\ 0 & (x \neq t ) \end{cases}
$$

$$
\int_{\infty}^{\infty} \delta(x-t)dx=1
$$

$$
\int_{\infty}^{\infty} f(x)\delta(x-t)dx=f(t)
$$

ヘヴィサイドステップ関数

$$
h(x)=\begin{cases} 1 & (x>0) \\ 0 & (x <0 ) \end{cases}
$$

微分するとデルタ関数

$$
\frac{dh}{dx}(x)=\delta(x)
$$

ヘヴィサイドステップ関数の入力値ずらす

$$
h(x-t)=\int_{-\infty}^{x} \sigma(x'-t)dx'
$$

$$
h(x-t)=\begin{cases} 1 & (x>t) \\ 0 & (x <t ) \end{cases}
$$

$$
\frac{dh(x-t)}{dx}=\delta(x-t)
$$

ラプラス方程式

$$
\nabla^2 u=0
$$

二次の場合

$$
\nabla^2 u  = \frac{\partial^2 u}{\partial x^2}+\frac{\partial^2 u}{\partial y^2}
$$

変数にtが入ってないので時間に応じて変化しない。
ラプラシアンはある地点とその周囲の平均とのズレを表す。
微分方程式なので解となる関数を探したりするわけだが、ラプラス方程式の解となる関数のことを調和関数という。

1次元ポアソン方程式のグリーン関数

1次元ポアソン方程式

がある時、

なるものがグリーン関数。

この時のグリーン関数はx=ξを除いて

の解である。すなわち

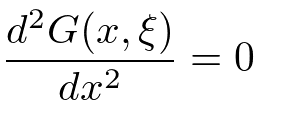
$$
\int_\Omega u\frac{\partial v}{\partial x_i} dx = \int_\Gamma uvn_i d\gamma -\int_\Omega \frac{\partial u}{\partial x_i}v dx \quad (1 \leqq i \leqq N)
$$

ヤコビ行列

微分という操作としてのヤコビ行列

ベクトル場をベクトルで微分したもの

$${\bm y = (y_1, y_2, …, y_m)}$$
$${\bm x = (x_1, x_2, …, x_n)}$$

これをヤコビ行列という。
m=1の時、勾配の転置に一致。

p470
スタンフォード ベクトル・行列からはじめる最適化数学 (KS情報科学専門書) 単行本（ソフトカバー） – ビッグブック, 2021/3/1
ステファン・ボイド (著), リーヴェン・ヴァンデンベルグ (著), 玉木 徹 (翻訳)

$$
\frac{\partial \bm y}{\partial \bm x}
=\begin{bmatrix}
\frac{\partial y_1}{\partial x_1} & \frac{\partial y_1}{\partial x_2} & \cdots & \frac{\partial y_1}{\partial x_n}\\
\frac{\partial y_2}{\partial x_1} & \frac{\partial y_2}{\partial x_2} & \cdots & \frac{\partial y_2}{\partial x_n}\\
\vdots &\vdots & \ddots & \vdots\\
\frac{\partial y_m}{\partial x_1} & \frac{\partial y_m}{\partial x_2} & \cdots & \frac{\partial y_m}{\partial x_n}\\
\end{bmatrix}
$$

あるいは

$$
J=J(\frac{\partial y}{\partial x})=(\frac{\partial y_j}{\partial x_i})
$$

座標変換の道具としてのヤコビ行列

$${\mathbb R^n}$$から$${\mathbb R^n}$$への変換関数
$${Y=g(X)}$$を考える。ここで関数$${g(x)}$$は

$$
g(x)
=\begin{bmatrix}
g_1(x)\\
g_2(x)\\
\vdots\\
g_n(x)\\
\end{bmatrix}
$$

例えば$${(x,y,z)}$$を変換するなら

$$
g(x,y,z)
=\begin{bmatrix}
g_x(x,y,z)\\
g_y(x,y,z)\\
g_z(x,y,z)\\
\end{bmatrix}
$$

$${Y=g(X)}$$とは逆に、YからXに変換可能な場合、
それを$${h(y)}$$とすると

$$
h(y)
=\begin{bmatrix}
h_1(y)\\
h_2(y)\\
\vdots\\
h_n(y)\\
\end{bmatrix}
$$

これでヤコビ行列が定義できて

$$
J(\frac{\partial x}{\partial y})=
\begin{bmatrix}
\frac{\partial h_1(y)}{\partial y_1} &\cdots&\frac{\partial h_1(y)}{\partial y_1}\\
\vdots&\ddots&\vdots\\
\frac{\partial h_n(y)}{\partial y_1} &\cdots&\frac{\partial h_n(y)}{\partial y_n}\\
\end{bmatrix}
$$

最初のものとx,yがひっくり返っているため、文脈に注意を要する。
添え字はxのnが基準なのでたぶん揃っている。

この行列の行列式はヤコビアンといい、座標変換に用いることができる。

ヤコビアン

xy平面上の領域Dにおける積分

$$
\iint_D f(x,y)dxdy
$$

を考える。

この積分が別のパラメータ領域Hにおいて
パラメータu,vを用いた時も成り立つための変換はどんなか。

例えば

$$
x=r cos \theta\\
y=r sin \theta
$$

は、パラメータ$${0<r}$$、$${0\leqq\theta<2\pi}$$をxy平面に写す。

このような変換一般を$${rcos\theta \to \phi(u,v)}$$,$${rsin\theta \to \psi(u,v)}$$と表すなら

$$
\iint_D f(x,y)dxdy=\iint_H f(\phi(u,v),\psi(u,v))|det A|dudv
$$

ここで$${det A}$$は

$$
\LARGE
\begin{vmatrix}
   \frac{\partial \phi}{\partial u} & \frac{\partial \phi}{\partial v} \\
   \frac{\partial \psi}{\partial u} & \frac{\partial \psi}{\partial v}
\end{vmatrix}
$$

こんなような変換関数の偏微分係数集めた行列の行列式をヤコビアンという。

ベルヌーイ分布:Bern(x;mu)

コイントス１回に関する分布。

コインの表裏のように、結果が２通りであるような試行をベルヌーイ試行という。この時、表裏に相当する確率変数Xは二値（例えば０と１、ここでは0が裏で1が表）をとる。しかしコインが削れているなどして、表裏の確立に偏りがある場合、
表の出現確率を$${\mu}$$とすると、裏の出現確率は$${1-\mu}$$
その確率質量関数は

$$
Bern(X=x|\mu)=\mu^x(1-\mu)^{1-x}
$$

上の式は$${\mu}$$と$${1-\mu}$$から作られるが、
逆に実際に値を代入してみると
確率変数の実現値が1、つまりコインが表になる確率は

$$
Bern(x=1|\mu)=\mu^1(1-\mu)^{1-1}=\mu
$$

確率変数の実現値が0、つまりコインが裏になる確率は

$$
Bern(x=0|\mu)=\mu^0(1-\mu)^{1-0}=1-\mu
$$

期待値

$$
E[x]=\mu
$$

分散

$$
V[x]=\mu(1-\mu)
$$

ベルヌーイ過程

連続したベルヌーイ試行の結果、
ある特定のパターンが得られる確率。

$$
P(X_1 = x_1, X_2 = x_2, ..., X_n = x_n) = \prod_{i=1}^{n}P(X_i = x_i) = \prod_{i=1}^{n}p^{x_i}(1-p)^{1-x_i}
$$

例えばある特定のパターン”11100”が得られる確率は、
パラメータ$${p=\frac{1}{2}}$$ならば$${(\frac{1}{2})^3(\frac{1}{2})^2}$$であって$${\frac{1}{32}}$$である。
パラメータ$${p=0.6}$$ならば$${(0.6)^3(0.4)^2}$$であって$${0.03456}$$である。

試行と分布と確率過程

ベルヌーイ試行はベルヌーイ分布に従う。
ベルヌーイ試行の結果を並べたものがベルヌーイ過程。

ベルヌーイ試行の結果を確率変数$${X=\lbrace 0, 1 \rbrace}$$とするなら、確率変数$${X}$$はベルヌーイ分布$${P(X = x) = p^x(1-p)^{1-x}}$$に従う。

パラメータの等しいベルヌーイ分布用いた複数回のベルヌーイ試行の結果、確率変数の列$${X_1, X_2,… X_n}$$の要素である確率変数$${X_i}$$は各々同一のベルヌーイ分布に従う。ここでパラメータの異なるベルヌーイ分布を用いた場合、同一分布とはみなされない。

ベルヌーイ試行を繰り返した時、最初の成功が起こるまでの試行回数$${X}$$は幾何分布に従う。

ベルヌーイ試行をn回実行した時の成功した（あるいはコインの表が出た）回数を$${H_n}$$回とするなら、確率変数$${H_n}$$は二項分布に従う。

ベルヌーイ試行がr回成功する（あるいはコインの表がr回出る）ために要した試行の回数を$${H_n}$$回とするなら、確率変数$${H_n}$$は負の二項分布に従う。

IID

確率変数の列（確率過程）における個々の確率変数は、各々ほかの確率変数に対して独立していなかったり、各々個別の分布に従っている場合がある。確率変数が独立、かつ各々同じ分布に従っているという仮定を独立同分布（ independent and identically distributed; IID, i.i.d., iid）という。

例えば、コイン投げやサイコロの投げなどはIIDプロセスの典型的な例です。各試行（コイン投げやサイコロの投げ）は他の試行から独立しており、全ての試行が同じ確率分布（コインの場合はベルヌーイ分布、サイコロの場合は一様分布）に従います。

ただし、現実の多くの現象やプロセスは完全にはIIDとは言えないこともあります。例えば、時系列データ（気温の変動、株価の変動など）では、時間的に近い観測値はしばしば相互に依存しているため、独立性の仮定が成り立たないことがあります。また、個々の観測が全て同じ分布に従うという仮定も、必ずしも真であるとは限りません。

同一分布である

パラメータが異なる場合、それらの分布は同一ではない。
例えば同一のコインをトスしていく過程は同一分布であろう。
しかしコインの表裏の確率に偏りがあり、トスのたびに異なる確率のコインを用いた場合、同一分布ではない。

連続したコイン投げがベルヌーイ分布に従ってベルヌーイ過程を成す、とは。同一のコインを用い、かつコインの摩耗などによる確率の変動がないことを前提とする。

二項分布:Bin(x;n,mu)

表の出現確率を$${p}$$、裏の出現確率を$${q=1-p}$$とすると$${p+q=1, q=1-p}$$
独立なベルヌーイ試行をn回した時、表が出る回数を確率変数Xとすると、
$${X=x(x=0,1,…,n)}$$となる確率質量関数は

$$
Bin(X=x|n,\mu)={}_nC_x\mu^x(1-\mu)^{n-x}
$$

あるいは

$$
P(X=x)=p(x)=\begin{pmatrix}
n\\
x\\
\end{pmatrix}\mu^x(1-\mu)^{n-x}={}_nC_x \mu^x(1-\mu)^{n-x}=\frac{n!}{x!(n-x)!}\mu^x(1-\mu)^{n-x}
$$

試行回数nと
表の確率$${\mu}$$
がパラメータとなる。

期待値

$${E[X]=n\mu}$$

分散

$${V[X]=n\mu(1-\mu)}$$

幾何分布:Geometric

ベルヌーイ試行が最初に成功するまでの試行回数が k 回 (k=1,2,3,...) である確率 $${P(X=k)}$$ は次の式で表されます。

$$
P(X=k) = (1 - p)^{(k - 1)} * p
$$

期待値

$$
E[X] = \frac{1}{p}
$$

分散

$$
Var[X] = \frac{1 - p}{p^2}
$$

これはつまり、成功の確率が高いほど（p が大きいほど）、成功するまでの試行回数は少なく（期待値が小さく）、ばらつきも小さく（分散が小さく）なるということです。

パスカル分布（負の二項分布）

幾何分布の一般化。

表の出現確率を$${p}$$、裏の出現確率を$${q=1-p}$$とすると$${p+q=1, q=1-p}$$
表がr回でるまでに必要な試行の回数kとすると、確率変数$${Y=k}$$は

$$
P(Y = k) = \binom{k-1}{r-1} p^r (1-p)^{k-r}
$$

に従う。ただし$${k\geq r}$$
$${r=1}$$の時、幾何分布。

期待値

$$
E[Y] = \frac{r}{p}
$$

分散

$$
Var[Y] = \frac{r(1-p)}{p^2}
$$

二項分布と負の二項分布

二項分布と負の二項分布（またはパスカル分布）は、どちらもベルヌーイ試行の結果に基づいていますが、考え方の焦点が異なります。

1. 二項分布：ある固定された回数nの試行において、成功する回数（例えばコイン投げで表が出る回数など）の確率分布を表します。つまり、「n回の試行でx回の成功が起こる確率は何か？」という問いに答えます。

2. 負の二項分布（パスカル分布）：ある固定された回数rの成功を得るために必要な試行の回数の確率分布を表します。つまり、「r回の成功を得るためには全体で何回の試行が必要か？」という問いに答えます。

二項分布は「試行回数が固定」で「成功回数が変数」なのに対し、負の二項分布は「成功回数が固定」で「試行回数が変数」です。この違いは、その名前が示す通りです：「二項」分布は二つの可能な結果（成功と失敗）がある一連の試行を表し、一方「負の二項」分布は成功が起こるまでの試行を数え続けることを表します。

したがって、これらの分布はベルヌーイ試行（成功/失敗の二択）を組み合わせたものと言えますが、視点の違いがその特性を定義します。

ポアソン分布:Poisson(x; lambda)

二項分布$${Bin(n,\mu)}$$における期待値を$${\lambda = n\mu}$$とし、
$${\lambda}$$を一定にした上で$${n\rightarrow \infty, \quad \mu \rightarrow 0}$$とした時の極限分布。

$$
P(X=x)=p(x)=\frac{\lambda^x e^{-\lambda}}{x!} \quad x=0,1,2…
$$

あるいは

$$
e^{-\lambda}\frac{\lambda^x }{x!}
$$

期待値

$${E[X]=\lambda}$$

分散

$${V[X]=\lambda}$$

指数分布:exp(x; lambda)

$$
f(x;λ) =
\begin{cases}
λe^{-λx} & \text{if } x >= 0, \\
0 & \text{if } x < 0.\\
\end{cases}
$$

期待値

$$
E[X] = \frac{1}{\lambda}
$$

分散

$$
Var[X] = \frac{1}{\lambda^2}
$$

期待値 E[X] はイベント間の平均待ち時間を表し、分散 Var[X] はその待ち時間のばらつきを表します。λが大きくなると、すなわちイベントが頻繁に起こると、待ち時間は短くなり、そのばらつきも小さくなります。一方、λが小さくなると、イベントがまれにしか起こらないため、待ち時間は長くなり、そのばらつきも大きくなります。

$${\lambda=\frac{1}{\lambda}}$$なら

$$
f(x;1/λ) =
\begin{cases}
\frac{1}{λ} e^{-\frac{x}{λ}} & \text{if } x >= 0, \\
0 & \text{if } x < 0.\\
\end{cases}
$$

この時

$$
E[X] = \lambda
$$

$$
Var[X] = \lambda^2
$$

一様分布:Uniform

サイコロの出目など。
全ての事象が同一の確率で発生するモデル。
確率変数の全ての実現値に等しい確率を割り振る分布。

離散型の場合

$$
P(X = x) = \frac{1}{n} \quad \text{for} \quad x \in {1, 2, ..., n} 
$$

これは、n個の結果すべてが等しい確率で発生することを表しています。

連続型の場合

確率変数Xの確率密度関数f(x)が

$$
f(x) = \begin{cases}
\frac{1}{b-a} & a\leq x \leq b \\
0 & {x\lt a  or  b \lt x}
\end{cases}
$$

これは、aからbまでの範囲で確率密度が一定であることを表しています。

累積分布関数は

$$
F(x) = \begin{cases} 0 & \text{for} \quad x < a \\
\frac{x - a}{b - a} & \text{for} \quad a \leq x < b \\
1 & \text{for} \quad x \geq b \end{cases}
$$

期待値

$$
E[X]=\frac{a+b}{2}
$$

分散

$$
V[X] = \frac{(b-a)^2}{12}
$$

正規分布:norm(x;mu, siguma^2)

ガウシアン

$$
Norm(x|\mu,\sigma^2)=\frac{1}{\sqrt{2\pi\sigma^2}}\exp\lbrace-\frac{1}{2\sigma^2}(x-\mu)^2\rbrace
$$

ないし

$$
f(x; μ, σ) = \frac{1}{\sqrt{2π}σ} e^{ - \frac{(x-μ)^2}{2σ^2} }
$$

$${(-\infty \lt x \lt \infty)}$$ではあるが、プログラムとかでは$${(x\lt -3, 3\lt x)}$$にも至らずに爆散する。

ベータ関数

$$
B(x, y) = \int_0^1 t^{x-1} (1-t)^{y-1} dt \quad (x>0, y>0)
$$

ガンマ関数を用いて次のように書くこともできます:

$$
B(x, y) = \frac{\Gamma(x)\Gamma(y)}{\Gamma(x + y)}
$$

ガンマ関数

階乗の一般化。
実数全体で定義され、その定義は次の通りです:

$$
\Gamma(z)=\int_0^\infty t^{z-1}e^{-t}dt \quad z>0
$$

特に、ガンマ関数は正の整数nについて、次の性質を持ちます:

$$
\Gamma(n)=(n-1)!
$$

ベータ関数

$$
B(x, y) = \frac{\Gamma(x)\Gamma(y)}{\Gamma(x + y)}
$$

について、正の整数m,nでガンマ関数を階乗で置き換えて

$$
B(m,n) = \frac{(m-1)!(n-1)!}{(m+n-1)!}
$$

二項係数

$$
\binom{n}{k} = \frac{n!}{k!(n-k)!}
$$

を用いると

$$
B(m,n) = \frac{1}{m+n-1}\binom{m+n-2}{m-1}
$$