電気回路（基礎）

記事を分割しました。

元記事

電気回路

ただし直流（定電圧、定電流）回路の場合。
広義の直流（定電圧、定電流）の振る舞いを考える場合、回路を構成する要素は抵抗のみと考えればよい。このモデルにおいて問題となるのは回路中の抵抗に流れる電流、回路中の抵抗にかかる電圧、抵抗の抵抗値である。

抵抗は電気を用いる豆電球なり機械なりと思えば良い。
またの名を負荷。

合成抵抗

ある区間、ある領域に抵抗が並んでいる場合、その区間にある抵抗をまとめて一つの抵抗と見ることができる。

直列の場合

単純に全部足す。

$$
R_0=R_1+R_2+…+R_n=\sum\limits_{i=1}^n R_i
$$

直列の場合、
電圧は各抵抗（負荷）の抵抗値に応じて分圧される。
電流はすべての抵抗（負荷）に等しく流れる。

並列の場合

合成抵抗の逆数は抵抗の逆数の和。
合成抵抗の逆数をコンダクタンス（電流の流れやすさ）と見ることもある。
つまり並列はコンダクタンスの和なので、電流が流れやすくなり、回路全体の電流が増える。

$$
R_0=\cfrac{1}{\cfrac{1}{R_1}+\cfrac{1}{R_2}+…+\cfrac{1}{R_n}}=\cfrac{1}{\sum\limits_{i=1}^n\cfrac{1}{R_i}}
$$

$$
\frac{1}{R_0}=\frac{1}{R_1}+\frac{1}{R_2}+…+\frac{1}{R_n}=\sum\limits_{i=1}^n\frac{1}{R_i}
$$

例えば$${10\Omega}$$の抵抗を並列に2つつないだ場合、
その合成抵抗は

$$
\frac{1}{R_0}=\frac{1}{10}+\frac{1}{10}=0.2\\
R_0=1/0.2=5\Omega
$$

であり、抵抗値は下がる。
抵抗値が下がるので回路の電流は増える。

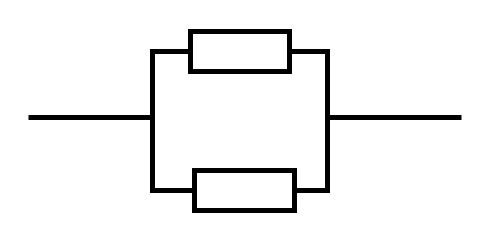
並列の場合、
電圧は各抵抗（負荷）に等しく掛かる。
電流は各抵抗（負荷）の抵抗値に応じて分流される。

基本的に抵抗を並列に繋いだら抵抗値は減るし、それに応じて回路の電流は増えるし、増えた電流が並列の各抵抗に分流される。

和分の積

並列に並んだ抵抗が２つだけの時、その区間の合成抵抗は簡易的に計算することができる。

$$
R_0=\frac{R_1R_2}{R_1+R_2}
$$

R_0は合成抵抗。

また、抵抗が並列に並んだ区間の合成抵抗は、和分の積を連発しても求めることができる。適当な区間に並んでいる抵抗を、ある部分の、ある区間の合成抵抗ということで括ってしまえば、最終的には２つの抵抗の直列か並列の回路に帰着できる。

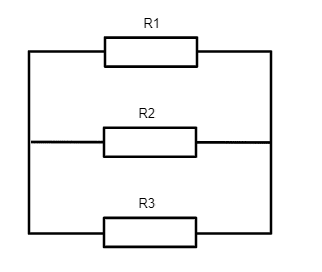
上と全く同じ回路

$$
R_0 = \frac{R_1 \left(\frac{R_2 R_3}{R_2 + R_3}\right)}{R_1 + \left(\frac{R_2 R_3}{R_2 + R_3}\right)} 
$$

$$
R_0 = \frac{R_1 R_2 R_3}{R_1 (R_2 + R_3) + R_2 R_3}
$$

$$
R_0 = \frac{R_1 R_2 R_3}{R_1 R_2 + R_1 R_3 + R_2 R_3}
$$

$$
R_0 = \frac{1}{\frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3}}
$$

分電圧

直列に抵抗が並んでいる区間に電圧をかけた場合、各々の抵抗には抵抗値に応じた電圧がかかる。

$$
V_i=V_0\frac{R_i}{R_0}
$$

$${V_0}$$は区間全体にかかる電圧
$${R_0}$$は区間全体の合成抵抗
$${R_i}$$は任意の抵抗１つ
$${V_i}$$はその任意の抵抗にかかる電圧

特に直列に並んだ抵抗が２つだけの時の分電圧は

$$
V_1=V_0\frac{R_1}{R_1+R_2}
$$

抵抗が並列に並んでいる場合は電圧はすべての抵抗に等しくV_0かかる。分圧されない。

また、分電圧が起きる場合、後ろの抵抗から見ると前の抵抗によって電圧が消費されたかのようにうつる。こういうのを電圧降下という。ある１つの負荷ないし抵抗の両端、ないしある区間の両端に掛かっている電圧、その区間で消費されたように映る電圧、というような感じである。
電圧降下のことを逆起電力ともいう。

wikipediaの言葉を借りれば、電圧降下とは回路中の負荷の両端に生じる電位差である。

分電流

日本語wiki

$$
I_i=I_0\frac{R_0}{R_i}
$$

あるいは英語wiki

$$
I_i=I_0\frac{\bar R_i}{R_i+\bar R_i}
$$

ただし$${R_i}$$のバー付きは$${R_i}$$以外の合成抵抗

例えば３つの並列抵抗の場合

$${R_i}$$のバー付きを使用した英語wikiの式の

$$
I_1 = I_0 \frac{\frac{R_2 R_3}{R_2 + R_3}}{R_1 + \frac{R_2 R_3}{R_2 + R_3}}
$$

に対し、分子分母に$${R_2+R_3}$$かけて

$$
I_1 = I_0 \frac{R_2 R_3}{R_1 R_2 + R_1 R_3 + R_2 R_3}
$$

分子分母を$${R_1R_2_R_3}$$で割る

$$
I_1 = I_0 \frac{\frac{1}{R_1}}{\frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3}}
$$

分子分母にR_1かけてのち、分母の塊で割ると日本語wikiの式

$$
I_1 = I_0 \frac{\frac{1}{\frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3}}}{R_1}
$$

特に並列に並んだ抵抗が２つだけの時の分電流は

$$
I_1 = I_0 \frac{R_2}{R_1 + R_2}
$$

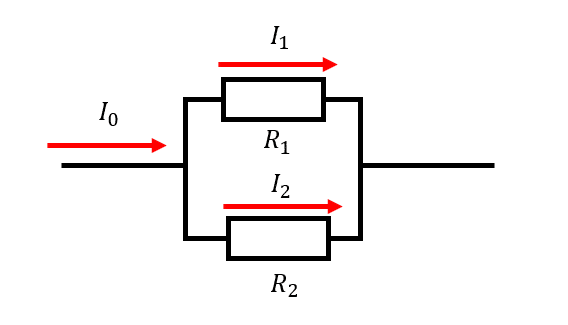
この式に和分の積を連発すると英語wikiの式となる。

抵抗が直列に並んでいる場合は電流はすべての抵抗に等しくI_0かかる。分流されない。

キルヒホッフ則

回路に成り立つ一般的な法則。

第１則

岐路に適用される。

回路中のある点における電流の総和は０。流入と流出は等しい。

$$
\sum I_n=0
$$

第２則

閉路に適用される。

閉回路内の電圧降下の総和は０。閉路の起電力の総和と電圧降下の総和は等しい。

起電力：電池とか発電機とかによる電圧。電位差を維持するもの。連続的に電流を流す原動力となるもの。

起電力を発生、供給するものを電源という。

$$
\sum E_n = \sum I_nR_n
$$

重ね合わせの理

起電力が複数ある場合、回路中の電圧及び電流は、その回路において起電力が各々単独で存在する場合を想定したのものを全部足したものに等しい。

回路は、起電力の個数分だけ分身でき、各々の分身回路の電圧及び電流を全部足したら元の回路の電圧及び電流が計算できる。

抵抗の値は分身した場合も統合した場合も同じであると考える。

電池

電池は内部抵抗を持つ起電力とも解釈することができる。

電池の端子電圧は

$$
V=E_0-IR_0
$$

で表される。
ここで起電力$${E_0}$$と内部抵抗$${R_0}$$が一定であると考えると、
回路に流れる電流$${I}$$に応じて、電池が供給する電圧は変化する。
具体的には負荷が軽く、回路の抵抗が低いほど$${I}$$が増加し、電池の端子から取り出せる電圧は低くなる。

この電源電圧の変動は、並列に接続された負荷がON/OFFされることで時に無視できない影響を及ぼす。

テブナンの定理

回路中の負荷に流れる電圧及び電流を求めたい時、その負荷以外の回路部分をぎゅっとまとめて上図の電池のように考えることができる。

ミルマンの定理

並列に並んだ電池みたいな回路は全部まとめて計算できる。

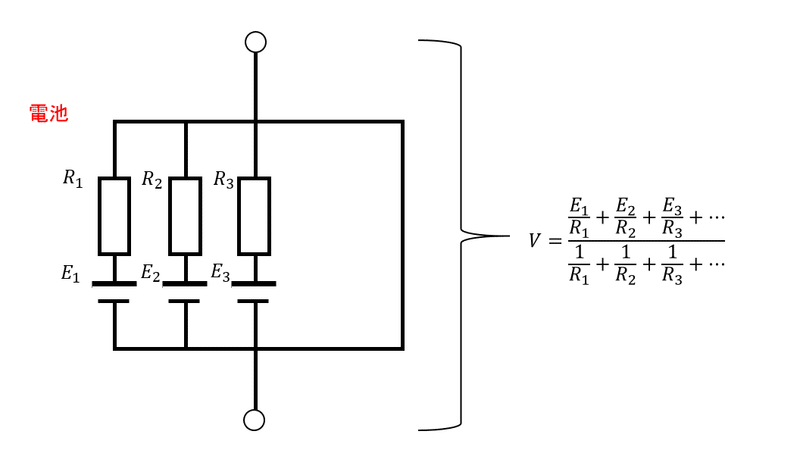
これは結局、並列の合成抵抗×並列回路に流れてる電流の総和

$$
V = \frac{1}{\frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + \cdots} \cdot (I_1 + I_2 + I_3 + \cdots)
$$

$$
V=R_0I_0
$$