統計基礎：代表値（要約統計量）

ヒストグラム

階級（Class)

統計学における「階級」は、一般的に、データを整理しやすいように範囲ごとに分けたグループのことを指します。これは、データの分布を理解するための重要な手段であり、特に大量のデータを扱う際に有用です。

たとえば、あるクラスの生徒全員の身長データを持っているとしましょう。その身長データは、150cmから190cmの間に分布しているとします。このとき、そのデータを階級に分けることができます。これを5cm刻みで階級を作ると、次のようになります：

$$
\begin{array}{|c|c|}
\hline
階級（身長） & 人数 \\
\hline
150〜154cm & 3 \\
\hline
155〜159cm & 7 \\
\hline
160〜164cm & 12 \\
\hline
165〜169cm & 20 \\
\hline
170〜174cm & 15 \\
\hline
175〜179cm & 10 \\
\hline
180〜184cm & 5 \\
\hline
185〜189cm & 2 \\
\hline
\end{array}
$$

これにより、各階級にどれくらいのデータ（生徒）が含まれているかを数えることができます。これは、データの分布の理解や視覚的な表現（例えばヒストグラム）に役立ちます。

階級の数や範囲を決めるときは、データの特性や目的によって変わります。階級を細かくすると、データの詳細な分布がわかりますが、大まかな傾向が見えにくくなる場合があります。逆に、階級を大きくすると、大まかな傾向はつかみやすくなりますが、詳細な情報が失われます。このため、階級の設定はデータ解析の目的に応じて適切に選ぶことが重要です。

google colabの場合

!pip install japanize-matplotlib
import matplotlib.pyplot as plt
import japanize_matplotlib 

# データの定義
height_ranges = ["150〜154", "155〜159", "160〜164", "165〜169", "170〜174", "175〜179", "180〜184", "185〜189"]
counts = [3, 7, 12, 20, 15, 10, 5, 2]

# ヒストグラムの作成
plt.bar(height_ranges, counts)

# タイトルとラベルの設定
plt.title("身長の階級別の人数")
plt.xlabel("身長の階級")
plt.ylabel("人数")

# ヒストグラムの表示
plt.show()

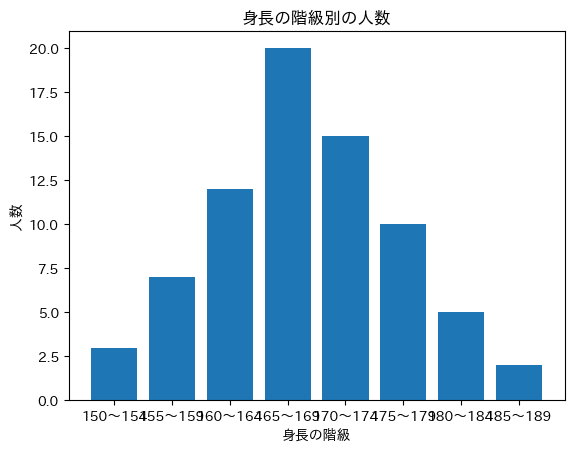
オブジェクトからヒストグラムを生成する場合

import matplotlib.pyplot as plt
import japanize_matplotlib
import numpy as np

# 名前と身長のデータ
data = {
    "田中": 152,
    "佐藤": 157,
    "鈴木": 165,
    "高橋": 172,
    "田村": 158,
    "井上": 160,
    "中村": 167,
    "山本": 175,
    "山田": 162,
    "岡田": 170
}

# 身長のリストを作成
heights = list(data.values())

# ヒストグラムの階級の範囲を設定 (150cmから180cmまで5cm刻み)
bins = np.arange(150, 185, 5)

# ヒストグラムの作成
plt.hist(heights, bins=bins, edgecolor='black')

# タイトルとラベルの設定
plt.title("身長の階級別の人数")
plt.xlabel("身長の階級")
plt.ylabel("人数")

# ヒストグラムの表示
plt.show()

階級値（Class mark）

階級値（Class Mark）は、各階級を代表する一つの値を指し、通常、その階級の下限値と上限値の平均値として計算されます。したがって、階級値はその階級の平均値と言えます。

例えば、「身長」を5cmの範囲で階級分けした場合、「150〜154cm」、「155〜159cm」、「160〜164cm」という階級になるかと思います。これらの階級の階級値はそれぞれ「152cm」、「157cm」、「162cm」となります（各階級の下限値と上限値の平均）。

階級値は、度数分布表を用いてデータの中心傾向を見る際によく使われます。例えば、各階級の度数と階級値を掛け合わせて総和をとり、それを全度数で割ることで、階級分布の平均値（階級平均）を求めることができます。

$$
\text{Class Mark} = \frac{\text{Lower Limit} + \text{Upper Limit}}{2}
$$

階級平均（Class mean）

階級平均は各階級の階級値とその階級の度数の積の合計を全度数で割ったものです。

$$
\text{Class Mean} = \frac{\sum (\text{Class Mark} \times \text{Frequency})}{\text{Total Frequency}}
$$

def class_mean(class_marks, frequencies):
    total_frequency = sum(frequencies)
    sum_of_products = sum([mark * freq for mark, freq in zip(class_marks, frequencies)])
    return sum_of_products / total_frequency

度数(Frequency)

統計学において、「度数」はデータセット内の特定の値または値の範囲（階級）が出現する回数を指します。たとえば、クラスで学生の身長を測定した場合、特定の身長範囲（例えば160-165cm）の学生が何人いるかを数えると、その数が度数になります。
度数は、度数分布表やヒストグラムを作成する際に特に重要です。度数分布表では、各階級とそれに対応する度数をリストします。ヒストグラムでは、x軸に階級、y軸に度数を取り、度数の高さに応じた棒グラフを描きます。これにより、データの分布や傾向を視覚的に理解することが可能になります。
なお、「相対度数」という用語もあり、これは全体の度数に対する特定の階級の度数の割合を示します。これにより、各階級が全体のどの程度を占めているかを理解することができます。

代表値

相加平均（Arithmetic Mean）

相加平均は、最も一般的な平均の計算方法で、全ての値の合計を値の数で割ったものです。数学的には次のように表されます。

$$
\text{Arithmetic Mean} = \frac{1}{n} \sum\limits_{i=1}^{n} x_i
$$

例えば、データセットが {4, 8, 6, 5, 3, 2, 8, 9, 2} の場合、相加平均は (4 + 8 + 6 + 5 + 3 + 2 + 8 + 9 + 2) / 9 = 5.22 となります。これは、各値が等しい重要性を持つときに使用されます。

import numpy as np

def arithmetic_mean(x):
    return np.mean(x)

あるいは

def mean_python(data):
    return sum(data) / len(data)

相乗平均（Geometric Mean）

相乗平均は、全ての値の積のn乗根（nは値の数）として計算されます。数学的には次のように表されます。

$$
\text{Geometric Mean} = \left( \prod\limits_{i=1}^{n} x_i \right) ^{\frac{1}{n}}
$$

例えば、データセットが {1, 10} の場合、相乗平均は (1 * 10) ^ (1/2) = 3.16 となります。相乗平均は、各値が乗算関係にある場合や、成長率や比率を扱うときなどに使用されます。具体的には、複利の平均成長率を計算する場合や、異なるスケールのデータを組み合わせる際に用いられます。

なお、一般的に相乗平均の値は相加平均の値よりも小さくなります（ただし全ての値が等しい場合を除く）。

import numpy as np

def geometric_mean(x):
    return np.prod(x)**(1.0/len(x))

あるいは

from functools import reduce
import operator

def prod_python(data):
    return reduce(operator.mul, data, 1)

調和平均（Harmonic Mean）

調和平均は、データセット内の値の逆数の算術平均の逆数として定義されます。数学的には次のように表されます。

$$
\text{Harmonic Mean} = \frac{n}{\sum\limits_{i=1}^{n} \frac{1}{x_i}}
$$

nは値の数、x_iは各値を表します。調和平均は、レートや比率の平均を計算するときに特に有用です。例えば、速度の平均値を計算する際には調和平均が使用されます。

import numpy as np

def harmonic_mean(x):
    n = len(x)
    return n / np.sum(1.0 / np.array(x))

対数平均（Logarithmic Mean）

対数平均は、2つの正の数 a と b の間の平均値を計算するために使用されます。数学的には次のように表されます。

$$
\text{Logarithmic Mean} = \frac{b - a}{\log b - \log a}
$$

これは、数値が乗法的な増加を示すとき（つまり比率や倍率が一定）や、対数正規分布などの対数で変換すると正規分布に従うようなデータに対して特に有用な平均値です。

両者とも算術平均や幾何平均とは異なる視点から「平均」を提供しますが、適用するべき具体的な状況は、扱っているデータの性質によります。

import numpy as np

def logarithmic_mean(a, b):
    return (b - a) / (np.log(b) - np.log(a))

中央値（Median）

データを昇順ソートした時の真ん中。
要素が偶数のときは真ん中二つを足して２で割った値。

$$
M = \begin{cases} x_{(n/2)} & \text{if } n \text{ is even} \\
\frac{x_{((n+1)/2)} + x_{((n-1)/2)}}{2} & \text{if } n \text{ is odd} \end{cases}
$$

def median(data):
    data.sort()
    n = len(data)
    if n % 2 == 0:
        median = (data[n//2 - 1] + data[n//2]) / 2
    else:
        median = data[n//2]
    return median

分位数(Quantile)

分位数とは、確率変数または確率分布を等分割する値を指します。あるデータセットにおいて、分位数はそのデータの分布や散らばり具合を理解するのに有用な工具となります。
例えば、四分位数は特殊な分位数で、データを4つの等しい部分に分けます。

• 第1四分位数 (Q1): 下から数えて25%の位置にある値

• 第2四分位数 (Q2): 下から数えて50%の位置にある値、つまり中央値（Median）

• 第3四分位数 (Q3): 下から数えて75%の位置にある値

また、パーセンタイルも分位数の一種で、100等分した位置の値を指します。例えば、90パーセンタイルは下から数えて90%の位置にある値です。
Pythonでは、Numpyのpercentileやquantile関数、Pandasのquantileメソッドなどを用いて分位数を計算することができます。

import numpy as np

# データの例
data = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10])

# 四分位数の計算
Q1 = np.percentile(data, 25)
Q2 = np.percentile(data, 50)
Q3 = np.percentile(data, 75)

# パーセンタイルの計算
P90 = np.percentile(data, 90)

最頻値(mode)

一番出現回数の多い値。
ヒストグラムの一番高い山の値

最頻値は、データセット内で最も頻繁に現れる値を指します。最頻値は数値データだけでなく、カテゴリーデータに対しても適用できます。なお、データセットによっては最頻値が存在しない場合や、複数存在する場合（これを多峰性といいます）もあります。

from scipy import stats

def mode(x):
    return stats.mode(x)[0][0]

あるいはcollections.Counterを用いて。

from collections import Counter

def mode_custom(x):
    counts = Counter(x)
    max_count = max(counts.values())
    modes = [item for item, count in counts.items() if count == max_count]
    return modes

Pythonのcollections.Counterは、データ内の要素の出現回数をカウントするための辞書型のサブクラスです。内部的には、ハッシュテーブル（Pythonの辞書型の実装に使われているデータ構造）を使って要素と出現回数を関連付けています。

出現範囲をあらかじめ定めて良い場合

def mode_python(a):
    hist = [0]*255
    for val in a:
        if 0 <= val < 255:
            hist[val] += 1
    return hist.index(max(hist))

//疑似コード
int mode(int[] a)
{
  int[] hist = new int[255]
  for(int i = 0; i<a.count; i++)
  {
    int val = a[i];
    if(0<=val && val < 255)
    {
      hist[val]++;
    }
  }
  return hist.indexOf(max(hist));
}

//この実装は、暗黙の内にデータの出現範囲を定めている。
//出現範囲が分かっているなら引数でとるとか
//出現範囲が分からないならmin,maxでその場で配列を作成するだとかが必要となる
//あるいは辞書にしてカウントするなどする

期待値(Expectation)

または平均。
いわゆる平均というと、値を全部足して個数で割るみたいな相加平均・算術平均を指すが、確率の場合は期待値を指す。
期待値の場合、算術平均でいう個数で割るの部分を0-1の確率が担当する。

あるデータの平均をとった場合、データは必ず平均より上か下か平均ピッタシの値に分割される。そのためデータの平均からの離れ具合（偏差）を全部足すと必ずゼロ。

確率変数の期待値

離散型確率変数の場合

$$
E[X]=\sum\limits_{i=1}^nx_ip_i
$$

あるいは

$$
[E[X] = \sum_{i} x_i P(X = x_i)
$$

連続型確率変数の場合

$$
E[X]=\int_{-\infty}^{\infty} xp(x)dx
$$

算術平均の場合

$$
mean=\frac{1}{n}\sum\limits_{k=1}^na_k
$$

//期待値の場合
//pは全部足して1であること。
double expectation(double[] x, double[] p)
{
  double sum = 0;
  for(int i = 0; i<x.count; a++)
  {
    sum+=x[i]*p[i];
  }
  return sum;
}

//算術平均の場合
double mean(double[] a)
{
  double sum = 0;
  for(int i = 0; i<a.count; a++)
  {
    sum+=a[i];
  }
  return sum/a.count;
}

関数の期待値

あるいは関数f(x)に対して、f(x)が離散型の分布ならば

$$
E(f)=\sum_x p(x_i)f(x_i)
$$

f(x)が連続ならば

$$
E(f)=\int p(x)f(x)dx
$$

例えばガウス分布の期待値は

$${p(x)=N(x|\mu, \sigma^2)}$$
$${f(x)=x}$$
として

$$
E[x]=\int_{-\infty}^\infty N(x|\mu, \sigma^2)x dx=\mu
$$

$${f(x)=x^2}$$とすると二次のモーメント

$$
E[x^2]=\int_{-\infty}^\infty N(x|\mu, \sigma^2)x^2 dx=\mu^2+\sigma^2
$$

期待値の演算規則

定数の期待値 : $${E(c) = c}$$
定数可算の期待値 : $${E(X+c)=E(X)+c}$$
定数倍の期待値 : $${E(cX) = cE(X)}$$
加法性 : $${E(X + Y) = E(X) + E(Y)}$$
線形性 : $${E(aX + bY) = aE(X) + bE(Y)}$$
確率変数が独立の時の積 : $${E(XY) = E(X)E(Y)}$$

確率変数が$${X_1, X_2, …, X_n}$$であって、確率分布がすべて共通なら期待値も等しい。$${E(X_1)=E(X_2)=…=E(X_n)=\mu}$$

また、期待値の加法性により

$${E(X_1+X_2+…+X_n)=E(X_1)+E(X_2)+…+E(X_n)=\mu+\mu+…+\mu=n\mu}$$

また、期待値の相加平均を

$$
\bar X=\frac{X_1+X_2+…+X_n}{n}
$$

とおくと

$$
E(\bar X)=E(\frac{X_1+X_2+…+X_n}{n})=\frac{1}{n}E(X_1+X_2+…+X_n)=\frac{1}{n}n\mu=\mu
$$

条件付き期待値

複数変数の関数f(x,y)に対して

$$
E_x(f|y)=\sum_x p(x|y)f(x)
$$

条件付き期待値の演算規則

定数の条件付き期待値 :
定数の条件付き期待値はその定数自体
$${E(a | Y) = a}$$

定数倍の条件付き期待値 :
定数倍の条件付き期待値は、元の条件付き期待値にその定数を掛けたもの
$${E(aX | Y) = aE(X | Y)}$$

和の条件付き期待値 :
確率変数の和の条件付き期待値は、各確率変数の条件付き期待値の和
$${E(X + Z | Y) = E(X | Y) + E(Z | Y)}$$

線形性 : 
$${E(aX+b|Y)=aE(X|Y)+b}$$

積の条件付き期待値 :
一般に、積の条件付き期待値は各確率変数の条件付き期待値の積とはなりません。しかしXとYが独立である場合、以下が成り立ちます。
$${E(XY | Z) = E(X | Z)E(Y | Z) (X and Y are independent)}$$

分散[Variance]

標本分散

標本分散は、データセットの値の分散を計算する方法の一つで、データセット内の各データ点とその平均値との差の二乗の平均値を計算します。

一般的に、標本分散の計算は次の手順で行われます：

1. データセットの算術平均（または期待値）を計算します。

2. 各データ点と平均との差を計算します。

3. それらの差の二乗を計算します。

4. それらの二乗の平均値を計算します。

数式で表すと、次のようになります：

$$
s^2 = \frac{1}{n} \sum_{i=1}^n (x_i - \overline{x})^2
$$

ここで、

• $${s^2}$$は標本分散

• $${n}$$ はデータ点の数

• $${x_i}$$​ はデータ点

• $${\overline{x}}$$ はデータ点の平均

です。

ただし、注意すべきなのは標本分散は、標本全体のデータから算出される分散であり、元の母集団全体の分散を適切に推定するためには、無偏分散を使用することが多いです。無偏分散では、分母が n ではなく n−1 となります。

# 標本分散
def sample_variance(data):
    n = len(data)
    mean = sum(data) / n
    variance = sum((xi - mean) ** 2 for xi in data) / n
    return variance

不偏分散

不偏分散は、母集団の真の分散を推定するための統計的な手法です。データセットが母集団からのランダムなサンプルであるとき、不偏分散は母集団の真の分散を不偏に推定します。

不偏分散の計算方法は標本分散と非常に似ていますが、一つ重要な違いがあります。それは、各データ点と平均値との差の二乗の平均を計算する際、分母がサンプルサイズnではなく、サンプルサイズから1を引いたn−1であることです。

不偏分散の計算式は次の通りです：

$$
s^2 = \frac{1}{n-1} \sum_{i=1}^n (x_i - \overline{x})^2
$$

ここで、

• $${s^2}$$は標本分散

• $${n}$$ はデータ点の数

• $${x_i}$$​ はデータ点

• $${\overline{x}}$$ はデータ点の平均

不偏分散を用いる理由は、サンプルの大きさが小さいときにおける分散の過小評価を防ぐためです。これは "Bessel's correction" とも呼ばれています。n−1 を使用することで、小さなサンプルでも母集団の真の分散をより正確に推定することが可能になります。

def unbiased_variance(data):
    n = len(data)
    mean = sum(data) / n
    variance = sum((xi - mean) ** 2 for xi in data) / (n - 1)
    return variance

バイアス

標本分散の期待値は母集団の分散より小さくなります。これがバイアスです。

$$
E[s^2] = E[\frac{1}{n} \sum_{i=1}^n (x_i - \bar{x})^2]\\
= \frac{1}{n} \sum_{i=1}^n E[(x_i - \bar{x})^2]\\
= \frac{1}{n} \sum_{i=1}^n (\sigma^2 - \frac{\sigma^2}{n})\\
= \sigma^2 - \frac{\sigma^2}{n}\\
= \frac{n-1}{n}\sigma^2
$$

不偏分散の場合、

$$
E[s_u^2] = E[\frac{1}{n-1} \sum_{i=1}^n (x_i - \bar{x})^2]\\
= \frac{1}{n-1} \sum_{i=1}^n E[(x_i - \bar{x})^2]\\
= \frac{1}{n-1} \sum_{i=1}^n (\sigma^2 - \frac{\sigma^2}{n})\\
= \sigma^2 - \frac{\sigma^2}{n-1}\\
= \sigma^2
$$

したがって、無偏分散の期待値は母集団の分散と一致します。このため、n−1 で割ることによりバイアスが除去され、無偏性が達成されるのです。

確率変数の分散

期待値からの離れ具合。
偏差の２乗の平均（期待値）

離散型確率変数の場合

$$
V[X]=\sum\limits_{i=1}^n(x_i-E[X])^2 p_i
$$

連続型確率変数の場合

$$
V[X]=\int_{-\infty}^{\infty}(x-E[X])^2p(x)dx
$$

あるいは両方について

$$
V[X]=E[(X-E[X])^2]
$$

これは２次の中心モーメント。
同じことだがf(x)の場合

$$
V(f)=E \lbrace (f(x)-E(f(x)))^2 \rbrace
$$

また、別の表現として
２乗の期待値ー期待値の２乗

これらは原点まわりのモーメントを用いて中心モーメントを表したもの。
一般に、中心モーメントは原点まわりのモーメントを用いて表現することができる。
期待値は１次のモーメントであるが原点まわりのモーメントである。
分散は２次のモーメントであるが中心モーメントである。

$$
V[X]=E[X^2]-\lbrace E[X] \rbrace^2
$$

$$
V(f)=E(f(x)^2)-E(f(x))^2
$$

また、偏差の２乗和、平方和を$${S_{xx}}$$とすると

$$
S_{xx}=\sum\limits_{i=1}^n(x_i-E(x))^2
$$

この時分散は

$$
V(x)=\frac{S_{xx}}{n}
$$

または

$$
V(x)=\frac{S_{xx}}{n-1}
$$

nで割ると標本分散。
n-1で割ると不偏分散。

分散の演算規則

定数の分散 : 
$${V(c)=0}$$

定数の可算 :
定数を加えることは分散に影響を及ぼしません。
$${Var(X + a) = Var(X)}$$

定数倍 :
確率変数を定数倍した時、その分散は二乗倍
$${Var(aX) = a^2 Var(X)}$$

加法性 : 
ただしXとYが独立の場合
$${ V(X\pm Y}=V(X)+V(Y)}$$

線形結合 :
ただしXとYが無相関（つまり$${Cov(X,Y)=0}$$）であること。
$${Var(aX + bY) = a^2 Var(X) + b^2 Var(Y)}$$

標準偏差[Standard Deviation]

$$
\sigma(X)=\sqrt{V[X]}
$$

２乗したものは平方根をとると単位が戻る。メートルが平方メートルになって、またメートルに戻るレベルで単位が戻る。

標準偏差は偏差(X-E(X))と単位が同じである。

標準偏差の方を基準にして、分散をσ^2とすることもある。

偏差

以下の部分が期待値からどれだけ離れているかの具体的な値。偏差という。

$$
X-E[X]
$$

分散は偏差の２乗和の期待値ということもできるのであるから、偏差がベクトル$${\bm x}$$で表されるとするなら内積による表記も可能。

$$
V=\frac{1}{n}(\bm x, \bm x)
$$

偏差という語は、あるデータとなにがしかの基準値との差というくらいの意味でしかないが、文脈によっては基準値がきめうちされていることがある。例えば上記のような期待値など。

なぜ２乗するか？

負値をとりたくないだけで、考え方としては絶対値でも良い。ただし絶対値だと計算がしづらいため２乗を取る。

離れ具合、すなわち与えられた分布の端が、期待値から見てより離れているか、より離れていないかを知りたい、比較したいだけならば分散だけを見ればよい。

共分散[Covariance]

分散を１変数の関数とみるなら共分散は２変数の関数。
共分散行列は多変数。

二組のデータの偏差の積の平均（期待値）
分散は自乗だが、共分散はデータの組の積。
二組のデータから、それなりに関連性を読み解くことができる指標となる。
どちらかというと、他の相関を求める手段の部品。
$${COV(X,Y)=0}$$ならば相関なし。
共分散を標準偏差の積で割ると相関係数。

分散$${V[X] = E[(X - E[X])^2]}$$において、
$${V[Z] = V[X + Y]}$$とおくと

$$
=E[(Z-E[Z])^2]\\
= E[((X+Y) - E[X+Y])^2]\\
$$

X, Yが独立であろうがなかろうが
$${E[X+Y]=E[X]+E[Y]}$$であるから

$$
= E[(X - E[X] + Y - E[Y])^2]\\
= E[(X - E[X])^2 + (Y - E[Y])^2 + 2*(X - E[X])(Y - E[Y])]\\
= E[(X - E[X])^2] + E[(Y - E[Y])^2] + 2E[(X - E[X])(Y - E[Y])]\\
= V[X] + V[Y] + 2Cov[X,Y]
$$

よって

$$
COV(X,Y)=E[(X - E[X])(Y - E[Y])]
$$

あるいは

$$
COV(X,Y)=E\lbrace(X-\mu_x)(Y-\mu_y) \rbrace
$$

あるいは

$$
COV(x,y)=E_{x,y}((x-E(x))(y-E(y)))\\
COV(x,y)=E_{x,y}(xy)-E(x)E(y)
$$

また、偏差の積和が$${S_{xy}}$$で表される時

$$
S_{xy}=\sum\limits_{i=1}^n(x_i-E(x))(y_i-E(y))
$$

ならば

$$
C_{xy}=\frac{S_{xy}}{n-1}
$$

多分この時のn-1は分散の時と同じ理屈であると思われるが不明。

共分散行列

$$
V(X+Y+Z) = V(X) + V(Y) + V(Z) + 2COV(X,Y) + 2COV(X,Z) + 2COV(Y,Z)
$$

$$
V(X_1 + X_2 + ... + X_n) = \sum_{i=1}^{n} V(X_i) + 2\sum_{i=1}^{n}\sum_{j=i+1}^{n} COV(X_i, X_j)
$$

これは対角より下をインデックスで走査して２掛けるタイプ。
あるいは

$$
V(X_1 + X_2 + ... + X_n) = \sum_{i=1}^{n} V(X_i) + \sum\sum_{i\neq j}^{n} COV(X_i, X_j)
$$

これは対角以外を走査するタイプ。

ある確率変数の列、および列ベクトル

$$
\bm X
=
\begin{bmatrix}
X_1\\
X_2\\
\vdots\\
X_n\\
\end{bmatrix}
$$

について

$$
\bm \Sigma= 
\begin{bmatrix}
E[(X_1-\mu_1)(X_1-\mu_1)] & E[(X_1-\mu_1)(X_2-\mu_2)] & \cdots & E[(X_1-\mu_1)(X_n-\mu_n)]\\
E[(X_2-\mu_2)(X_1-\mu_1)] &E[(X_2-\mu_2)(X_2-\mu_2)]& \cdots  & E[(X_2-\mu_2)(X_n-\mu_n)]\\
\vdots & \vdots & \ddots & \vdots\\
E[(X_n-\mu_n)(X_1-\mu_1)] & E[(X_n-\mu_n)(X_2-\mu_2)] & \cdots & E[(X_n-\mu_n)(X_n-\mu_n)]\\
\end{bmatrix}
$$

$$
\bm \Sigma =
\begin{bmatrix}
V[X_1] & Cov[X_1,X_2] & \cdots & Cov[X_1, X_n]\\
Cov[X_2, X_1] & V[X_2] & \cdots & Cov[X_2, X_n]\\
\vdots & \vdots & \ddots & \vdots\\
Cov[X_n, X_1] & Cov[X_n, X_2] & \cdots & V[X_n]
\end{bmatrix}
$$

相関係数

共分散$${Cov}$$を標準偏差$${\sigma_X, \sigma_Y}$$の積で除す。
相関係数は０～１をとる。
-1方向が負の相関
0で相関なし
+1方向が正の相関

$$
\rho = \frac{Cov[X,Y]}{\sigma_X\sigma_Y}\\
Cov[X,Y]=\rho\sigma_x\sigma_y
$$

共分散と分散で表すと

$$
\rho=\frac{Cov[X,Y]}{\sqrt{V[X]V[Y]}}
$$

$$
\rho = \frac{E[(X-E[X])(Y-E[Y])]}{\sqrt{E[(X-E[X])^2]E[(Y-E[Y])^2]}}
$$

また、偏差の２乗和、平方和を$${S_{xx}}$$とすると

$$
S_{xx}=\sum\limits_{i=1}^n(x_i-E(x))^2
$$

また、

標準化されたデータ同士を内積してデータの個数で除す

$$
r=\frac{1}{n}(\bm z_1, \bm z_2)
$$

直交＝内積０の場合、２つのデータは無相関。

モーメント

全ての次数のモーメントが判明すれば、その分布は唯一完全に特定できる。
モーメントがないやつもおる。
また、普通は２次くらいまでを用いる。
これは感覚的にはテイラー展開を２次までで近似するのと似たようなもんである。

確率論と統計学において、モーメント（moment）は、確率分布またはデータセットの特性を捉えるための一つの指標で、確率変数やデータセットの形状や特性を表します。

原点まわりのモーメント（raw moment）

n次の原点まわりのモーメントは、確率変数Xのn乗の期待値として定義されます。

$$
E[X^n]
$$

ここで、Eは期待値を表します。
n=1の時、1次の原点まわりのモーメントは期待値そのものです。

中心モーメント（central moment）

n次の中心モーメントは、確率変数Xからその平均（期待値）を引いたものをn乗した期待値として定義されます。

$$
E[(X-\mu)^n]
$$

あるいは

$$
E[(X-E[X])^n]
$$

1次の中心モーメント : これは０です：

$$
E[(X - \mu)^1]
$$

あるいは

$$
E[(X - E[X])^1]
$$

これは

$$
E[(X - \mu)^1]=E[X]-E[E[X]]=E[X]-E[X]=0
$$

期待値の出力は定数。定数の期待値は定数。
例えば$${E[X]=c}$$の時、$${E[E[X]]=E[c]=c}$$
よって$${E[E[X]]=E[X]}$$

2次の中心モーメント（分散）: これは各データ点が平均からどれくらいばらついているかを示します。数式で表すと：

$$
V[X]=\sigma^2 = E[(X - \mu)^2]
$$

あるいは

$$
V[X]=E[(X - E[X])^2]
$$

原点まわりのモーメントを用いて表すと

$$
V[X]=E[X^2] - (E[X])^2
$$

3次の中心モーメント（歪度）: これは分布がどの方向に偏っているか（歪んでいるか）を示します。数式で表すと：

$$
\gamma_1 = E\left[\left(\frac{X - \mu}{\sigma}\right)^3\right]
$$

あるいは

$$
\mu'_3 = E[(X - \mu)^3] = E[X^3] - 3\mu E[X^2] + 2\mu^3
$$

同じことだが

$$
\mu'_3 = E[(X - E[X])^3] = E[X^3] - 3E[X]E[X^2] + 2(E[X])^3
$$

4次の中心モーメント（尖度）: これは分布がどれだけピークに集中しているか（または平坦か）を示します。数式で表すと：

$$
\gamma_2 = E\left[\left(\frac{X - \mu}{\sigma}\right)^4\right] - 3
$$

σで割る操作は「標準化」と呼ばれ、この操作によって単位に依存しない比率を得ることができます。なお、尖度の定義式における-3は、正規分布の尖度を0に調整するための補正項です。

あるいは

$$
\mu'_4 = E[(X - \mu)^4] = E[X^4] - 4\mu E[X^3] + 6\mu^2 E[X^2] - 3\mu^4
$$

同じことだが

$$
\mu'_4 = E[(X - E[X])^4] = E[X^4] - 4E[X]E[X^3] + 6(E[X])^2E[X^2] - 3(E[X])^4
$$