積分：よく忘れるヤツ、及びワケ分からんなるヤツ、こまいヤツ。あと力学。

まだ途中なるもの。

これは関数f(x)

原始関数を微分すると元の関数

f(x)を不定積分すると原始関数と積分定数

f(x)を定積分すると原始関数の差

微分積分学の基本定理

微分積分学の基本定理は2つの重要な定理から成り立っています。それらは「第一の基本定理」と「第二の基本定理」として知られています。

その１

実数値関数の積分が新しい関数を作り出し、その新しい関数の微分は元の（積分前の）関数を再生する。正確には、もし関数$${f}$$ が区間$${[a,b]}$$上で連続ならば、任意の実数$${x}$$ に対して、

$$
F(x) = \int_a^x f(t) \, dt
$$

なる新しい関数$${F}$$を生成する。この時、$${F}$$は区間$${[a,b]}$$上で微分可能であり、その導関数は元の（積分前の）関数$${f}$$に等しい。すなわち

$$
F′(x)=f(x)
$$

その２

与えられた関数が微分可能で、その導関数が特定の区間で連続である場合、その関数の導関数の積分は元の（微分前の）関数の差に等しい。

より正確には、 $${f}$$ が$${[a,b]}$$上で微分可能で、その導関数 $${f′}$$ が同じ区間で連続である時、任意の実数 $${x}$$に対して $${a≤x≤b }$$が成り立つならば、次の等式が成り立ちます。

$$
\int_a^b f'(x)  dx = f(b) - f(a)
$$

位置と速度と微分と積分

参考

力学 第2版 (物理学スーパーラーニングシリーズ)

位置を微分すると速度

速度を定積分すると位置の差の距離

速度一定ならばはじき

速度が一定でなくとも、平均をとれば強制的に一定

加速度及び自由落下の場合

加速度は速度の微分、位置の２階微分

定積分すると速度の差

不定積分の場合

参考

スタンフォード物理学再入門　力学

重力加速度は等加速度、すなわち加速度一定。地球上なら時間に応じて9.80665 m/s^2だけ速度に加算される。加速度が一定の場合、速度から見ると加速度は時間毎に加算される。

この時の速度の積分、原始関数は位置

速度の定積分により距離あるいは位置の変位

運動

運動：時間に応じた位置の変化。
速度：単位時間当たりの位置の変化。v
質量：運動したがらない能力。m
運動量：運動する物体の止めにくさ。p=mv
力：運動させる能力。単位時間当たりの運動量。F=ma=dp/dt
力積：時間に応じた運動量を変化さす力。F=ma=dp/dtの両辺積分
仕事：力と変位の積。内積。仕事が大ならば力か変位のどちらかないし両方が大。どちらかが０ならば０。単位時間当たりの運動量と位置の変化の積。W=Fx
エネルギー：仕事ができる能力。
運動エネルギー：運動量に依存するエネルギー。力が物体に仕事してる時に変化してる量。単位時間当たりの仕事。K=1/2mv^2
保存力：経路によらず一定の仕事をする力。重力。クーロン力。ばねの弾性力。
位置エネルギー：位置に依存するエネルギー。位置に応じて物体の成す仕事の量が異なる場合、位置に応じて物体にはエネルギーが蓄えられていると考える。
ポテンシャルエネルギー：位置エネルギー。

運動量

運動方程式

$${\bm F=0}$$の時、式を成り立たせるためには$${\bm a = 0}$$となる。
$${m=0}$$は数学的に存在するが、物理的には存在しないとみなされる。

運動エネルギー

力が仕事してる時に変化してる量。

仕事の分だけ変化してる量。

運動している物体は、静止するまで仕事を成すことができる。その、仕事を成すことができる能力がエネルギー。

p35

力学 (講談社基礎物理学シリーズ)

Fvは単位時間当たりの仕事（下記参照）
左辺：単位時間当たりの仕事＝右辺：単位時間当たりの運動エネルギー

avないしva部分(速度加速度)から1/2を生み出す変換はv^2を合成関数の微分で処理するとでてくるやつを用いる。

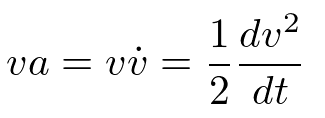
あるいは
p53

単位が取れる力学ノート (ＫＳ単位が取れるシリーズ)

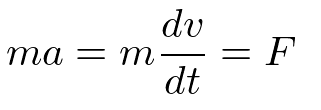
から

として

ここで仕事

ならば

運動量1が仕事すると運動量2に変化する。

仕事

質点が力によって位置が変化した場合

力一定で位置が変化する場合

単位時間当たりの仕事は両辺tで微分して

位置に応じて力も変化する場合

力の向きと位置の変位の方向が揃っていない場合
ベクトルの内積となる。

力積

時間に応じて力が変化する場合
質点の運動量の変化
F=maの両辺を定積分

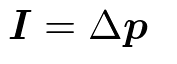
保存力

仕事は物体に力が掛かり、物体の位置が動いた時に発生する。その際に位置の経路が仕事に影響を与えないような力を保存力という。例えば重力、電磁気力等、空間中に万遍なく、全体攻撃のように掛かっている力の成す仕事は物体の経路に依存しない。

この場合、保存されているのは仕事。
保存力は重力、電気力。

保存力でないものは例えば摩擦力や空気抵抗。摩擦力が成す仕事は経路毎の摩擦具合に依存する。

また保存力は、適当な位置に移動して戻ってきた時の仕事の総和が０であるともいえる。

例えば重力は、ある物体の落下時、その経路に寄らずmghの仕事を成す。
物体を引き上げる時、-mghの仕事をして総計０
mは質量、gは重力加速度、mgで重力。hは高さ。

位置エネルギー＝ポテンシャルエネルギー

保存力は経路に寄らないので、保存力によって成される仕事は位置のことだけ考えればよい。このような、位置に応じた物体の仕事をする能力のことを位置エネルギーという。

力学的エネルギー

運動エネルギーと位置エネルギー（保存力）を足したやつ。K+U。

運動エネルギーはされた仕事の分だけ変化する。
力学的エネルギーは保存力に仕事をされても変化しない。
力学的エネルギーは非保存力にされた仕事の分だけ変化する。

力学的エネルギー保存則

保存則

ある量に関して、系の内外の釣り合いを見る。
例えば質量に関して

運動量に関して、運動方程式は

あるいは

などであるが、Fが０になると運動量の保存則。
外力の作用が無ければ運動量は一定に保たれるの法則。

一番分かり易いのは、保存される量に対してその変位が０の形をとるもの。
変位＝０
微分＝０のやつ。

積の微分

2つの関数f(x),g(x)の掛けたヤツの微分

不定積分の部分積分

積の微分を両辺積分すると不定積分の部分積分
式中にインテグラルが残っている場合は積分定数は書かなくて良い。多分、書いても良い（多分）。
最終的にインテグラルが全部消えた時に、最後に出現する積分定数に全部まとめる予定なのだと考える。つまりまだ時期が悪い。

定積分の部分積分

f={f(x)g(x)}'の原始関数はF={f(x)g(x)}

例えばガンマ関数の場合

なる妖怪みたいな公式を

とみて、各々ポケモンみたいに進化させると

であるからして、牌が揃ったのでドンジャラみたいに並べると

合成関数の微分

入力が関数である関数を微分するヤツ
2つの関数f(t),g(x)があり、t=g(x),の時
参考

数学大百科事典 仕事で使う公式・定理・ルール127

同じことだが別の表記

定積分の置換積分

積分の微小変位がdxからdtに切り替わるヤツ
入力の領域が変わるヤツ
参考：
x=h(t)タイプ
工科系の微分積分学の基礎p97
力学・電磁気学・熱力学のための基礎数学p40

力学・電磁気学・熱力学のための 基礎数学

（t=g(x),x=h(t)の両タイプ載ってる）
高校生のための逆引き微分積分　関数から判る解法のテクニックp26

高校生のための逆引き微分積分　関数から判る解法のテクニック (ブルーバックス)

理系のための　微分・積分復習帳　高校の微積分からテイラー展開までp135

理系のための 微分・積分復習帳 高校の微積分からテイラー展開まで (ブルーバックス)

の時、置換積分

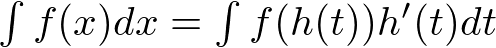
f(x)=x(x+1)なるを積分するにx+1をtとおいて……みたいな文脈の置換積分はg(x)の方の公式を用いる。t=x+1からt-1=xとおくとh(t)。

導出あるいは証明：F(x)に対する合成関数の微分、あるいは連鎖律から以下の通りとなるのでそこから両辺積分すると置換積分

最左辺と最右辺をxで積分

左辺は単純に積分と微分が帳消し

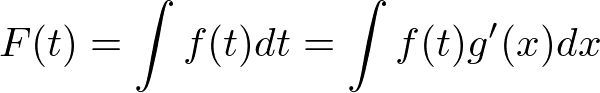
重積分

積分したい関数の入力が増えたなら積分する関数も増える

微小な面積に着目すれば領域の形状は何でもよくなる

ここでsは面。下記の弧長や線素とは別。

スカラー場の線積分

場と曲線が与えられた時、曲線に沿って場を積分する。

弧長形式の場合

弧長s

曲線上の２点間の距離（長さ）
２点のうち１点は固定して考え、簡単に考えるなら１点は始点として考える。残る１点は終点に向かって曲線上を動くと考える。

線素ds

弧長の差、弧長の微小変位。

ふまえると式の右辺は

長さを指定すれば曲線上の１点は明確に指定できるから、長さを入力として座標を出力し、それをもってスカラー場の入力にするというのは考え方としては成立する。しかしこれが実現できるのは曲線の具体的な全長が分かっていたり、曲線に丁寧なメモリが振ってある時。あるいは物差しで苦もなく測れる時であって、長さ入力というのは意外と使いづらいというのも分かる。

媒介変数形式の場合

媒介変数表示は曲線の視点をt=0,終点をt=1とするので、曲線の具体的な長さに関する情報は必要としない。

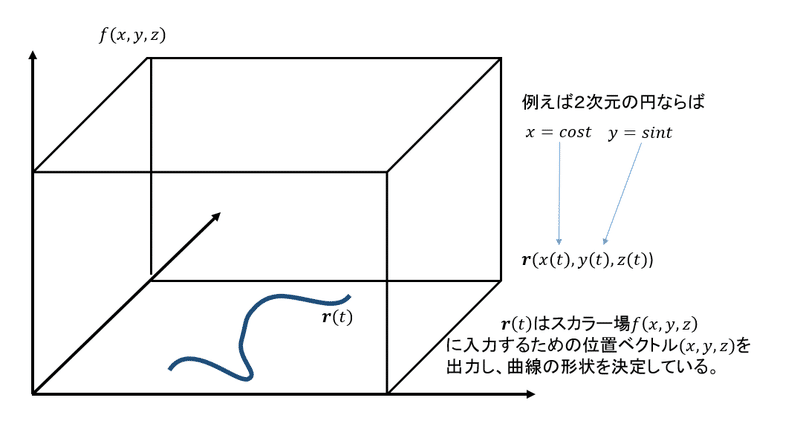
この時、線素dsはパラメータtの微小な変化に応ずる。すなわち短冊の下辺はtの変位に応じ、高さはその時のtに応ずる。弧長入力の時は下辺はある意味で一律で、高さは下辺に応じていた。

この時線素は

というふうに対応していて、それは下記のような感じだからである。

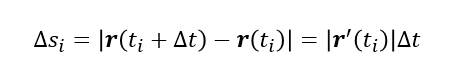
周回積分

曲線が閉じていて、閉路を成す場合の線積分。

ベクトル場の線積分

ドットは内積

スカラー場の面積分

重積分の１つ。とりわけ曲面上で積分をとりたい時。

Sは曲面、Dは積分領域

ベクトル場の面積分

ガウスの発散定理

体積分と面積分がくっつく。

ある３次元領域の単位体積当たりの発散（＝湧き出し・吸い込み）を全部足すと、３次元領域の境界となる表面から出たり入ったりした量に一致する。
右辺は単位面積当たりが担うベクトル場Ａの成分を全部足したもの。nは微小面の単位法線であり、長さ１の単位ベクトルとの内積は、あるベクトルがその単位ベクトル方向に落とす射影であり、あるベクトルから単位ベクトル方向に掛かっている成分である。

グリーンの定理

ストークスの定理の特別な場合。
平面領域Ｄの面積分と、その境界である閉曲線Ｃの線積分がくっつく。

参考

ベクトル解析（基礎解析学コース） 単行本 – 1995/10/25矢野 健太郎 (著), 石原 繁 (著) p75
理工系の数理 ベクトル解析 単行本 – 2020/11/18 山本 有作 (著), 石原 卓 (著) p87,129

とくに上式を平面におけるグリーンの定理という人もいる。

高校生からわかる複素解析 単行本 – 2018/9/12涌井 良幸 (著) p265
高校生からわかるベクトル解析 単行本 – 2017/12/27涌井 良幸 (著) p281

グリーンの公式と呼ぶ人もいる。

スッキリわかる複素関数論―誤答例・評価基準つき 単行本 – 2007/10/1皆本 晃弥 (著) p179
複素関数論の基礎 単行本 – 2015/11/28 山本 直樹 (著) p17

上式をグリーンの定理とし、それを変形した難しいやつをグリーンの公式としている人もいる。

スッキリわかる微分方程式とベクトル解析―誤答例・評価基準つき 単行本 – 2007/5/1 皆本 晃弥 (著) p210-
大学演習 ベクトル解析（矢野健太郎、石原繁 共著） 大学演習新書 Kindle版矢野 健太郎 (著), 石原 繁 (著) 形式: Kindle版 p231

おそらくその難しいやつをもってグリーンの公式としているであろう人もいる。

有限要素法の数理―数学的基礎と誤差解析 (計算力学とCAEシリーズ) 単行本 – 1994/12/1 菊地 文雄 (著) p251

ストークスの定理

曲面Ｓの面積分と、その境界の閉曲線Ｃの線積分がくっつく。