三角関数まわり

ChatGPT君まかせ。

基本

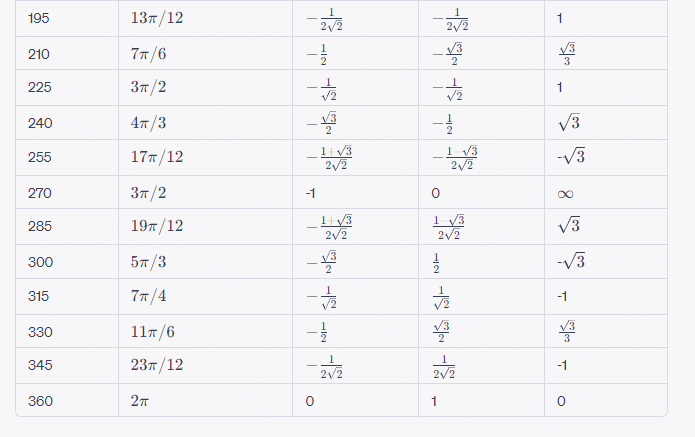
余弦、正弦、正接の範囲

$$
 -1 \leq \sin(x) \leq 1 \\
 -1 \leq \cos(x) \leq 1 \\
 -\infty < \tan(x) < \infty
$$

ただし$${ x \neq \frac{\pi}{2} + k\pi }$$（$${ k }$$は整数）

単位円の定義

$${ \sin(\theta) = y }$$座標
$${ \cos(\theta) = x }$$座標
$${ \tan(\theta) = \frac{y}{x} }$$

基本的な関係:

$$
\tan(x) = \frac{\sin(x)}{\cos(x)} 
$$

$$
1 + \tan^2 \theta = \frac{1}{\cos^2 \theta}
$$

ピタゴラスの定理

$$
\sin^2(x) + \cos^2(x) = 1 
$$

正弦定理

$${ \frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} = 2R }$$
ここで、$${ a, b, c }$$ は三角形の辺の長さ、$${ A, B, C }$$ はそれぞれの角度、$${ R }$$ は外接円の半径です。

余弦定理:

$${ c^2 = a^2 + b^2 - 2ab \cos C }$$
$${ b^2 = a^2 + c^2 - 2ac \cos B }$$
$${ a^2 = b^2 + c^2 - 2bc \cos A }$$
ここで、$${ a, b, c }$$ は三角形の辺の長さ、$${ A, B, C }$$ はそれぞれの角度です。

加法定理

$$
\sin(a+b) = \sin(a)\cos(b) + \cos(a)\sin(b) \\
 \cos(a+b) = \cos(a)\cos(b) - \sin(a)\sin(b) \\
 \tan(a+b) = \frac{\tan(a) + \tan(b)}{1 - \tan(a)\tan(b)} 
$$

負角・余角

$$
\cos(-\theta) = \cos\theta \\
\sin(-\theta) = -\sin\theta \\
\cos\left(\frac{\pi}{2} - \theta\right) = \sin\theta \\
\sin\left(\frac{\pi}{2} - \theta\right) = \cos\theta
$$

二倍角

$$
 \sin(2a) = 2\sin(a)\cos(a) \\
 \cos(2a) = \cos^2(a) - \sin^2(a) \\
 \tan(2a) = \frac{2\tan(a)}{1 - \tan^2(a)} 
$$

半角

$$
\sin\left(\frac{a}{2}\right) = \pm\sqrt{\frac{1 - \cos(a)}{2}} \\
\cos\left(\frac{a}{2}\right) = \pm\sqrt{\frac{1 + \cos(a)}{2}} \\
\tan\left(\frac{a}{2}\right) = \pm\sqrt{\frac{1 - \cos(a)}{1 + \cos(a)}} 
$$

ヘロンの公式

ヘロンの公式は、与えられた三角形の三辺の長さを使用してその面積を求めるための公式です。

三角形の三辺の長さを $${a}$$、$${b}$$、そして $${c}$$ とすると、半周の長さ $${s}$$ は以下のように求められます：
$${ s = \frac{a + b + c}{2} }$$

この半周の長さ $${s}$$ を使用して、三角形の面積 $${A}$$ はヘロンの公式を用いて以下のように求められます：

$${ A = \sqrt{s(s - a)(s - b)(s - c)} }$$

微分積分

sin

$${ \frac{d}{dx} \sin(x) = \cos(x) }$$
$${ \int \sin(x) dx = -\cos(x) + C }$$

sin(xy)

$${ f(x) = \sin(xy) }$$の場合。
合成関数の微分、すなわち連鎖律（Chain Rule）を使用します。
まず、$${ \frac{d}{dx}\sin(xy) }$$において$${ u = xy }$$と置きます。
このとき$${ \frac{du}{dx} }$$は$${ \frac{du}{dx} = y }$$
ただし$${ y }$$が$${ x }$$の関数である場合（$${ y }$$が$${ x }$$に依存する場合）は$${ \frac{du}{dx} = y + x\frac{dy}{dx} }$$
次に、$${ \frac{d}{dx}\sin(u)=\cos(u) }$$
最後に連鎖律$${\frac{d}{dx}f(g(x)) = f'(g(x)) \cdot g'(x)}$$を適用します。

$$
\frac{d}{dx}\sin(xy) = y\cos(xy)
$$

ただし$${ y }$$が$${ x }$$に依存する場合は

$$
\frac{d}{dx}\sin(xy) = \cos(xy) \cdot \frac{du}{dx} \\
 = \cos(xy) \cdot (y + x\frac{dy}{dx}) 
$$

sin(1/x)

$$
\frac{d}{dx}\sin\theta=\cos\theta\\
\frac{d}{dx}\frac{1}{x}=-\frac{1}{x^2}
$$

$$
\sin\frac{1}{x}=-\frac{1}{x^2}\cos\frac{1}{x}
$$

sin(y/x)

$${ f(x) = \sin\left(\frac{y}{x}\right)}$$
まず$${ u = \frac{y}{x} }$$と置きます。
$${ u }$$に対する$${ x }$$の微分は次のように計算できます。
$${ \frac{du}{dx} = -\frac{y}{x^2} }$$
次に$${ \sin(u) = \cos(u) }$$。
よって

$$
\frac{d}{dx} \sin\left(\frac{y}{x}\right) = \cos\left(\frac{y}{x}\right) \cdot \left(-\frac{y}{x^2}\right) = -\frac{y}{x^2} \cos\left(\frac{y}{x}\right) 
$$

sin(√x)

$$
\frac{d}{dx}\sin\theta=\cos\theta\\
\sin \sqrt{x} =\frac{1}{2\sqrt{x}}
$$

$$
\sin\sqrt{x} =\frac{1}{2\sqrt{x}}\cos\sqrt{x}
$$

cos

$$
\frac{d}{dx} \cos(x) = -\sin(x)\\
\frac{d}{dx}\cos(xy) = -y\sin(xy) \\
\frac{d}{dx}\cos\left(\frac{1}{x}\right) = \frac{1}{x^2}\sin\left(\frac{1}{x}\right) \\
\frac{d}{dx}\cos(\sqrt{x}) = -\frac{1}{2\sqrt{x}}\sin(\sqrt{x}) \\
\int \cos(x) dx = \sin(x) + C
$$

tan

$$
\tan(x) = \frac{\sin(x)}{\cos(x)}
$$

$${\frac{d}{dx} \tan(x) = \sec^2(x)}$$
$${\int \tan(x) dx = -\ln|\cos(x)| + C}$$

もしくは、以下のようにも表現されることがあります（$${\ln}$$は自然対数、$${ \ln|\sec(x)| }$$と$${ -\ln|\cos(x)| }$$は等価です）:

$$
\int \tan(x) dx = \ln|\sec(x)| + C
$$

$${\frac{d}{dx} \tan(x) = \sec^2(x)}$$の導出

商の微分$${\frac{d}{dx}\left(\frac{f(x)}{g(x)}\right) = \frac{f'(x)g(x) - f(x)g'(x)}{g^2(x)}}$$から

$$
\frac{d}{dx}\tan(x) = \frac{d}{dx}\left(\frac{\sin(x)}{\cos(x)}\right) = \frac{\cos(x)\frac{d}{dx}\sin(x) - \sin(x)\frac{d}{dx}\cos(x)}{\cos^2(x)}
$$

$${ \frac{d}{dx}\sin(x) = \cos(x) }$$および$${ \frac{d}{dx}\cos(x) = -\sin(x) }$$を用いて、

$$
= \frac{\cos(x)\cdot\cos(x) - \sin(x)(-\sin(x))}{\cos^2(x)} = \frac{\cos^2(x) + \sin^2(x)}{\cos^2(x)}
$$

ピタゴラス$${ \cos^2(x) + \sin^2(x) = 1 }$$から

$$
= \frac{1}{\cos^2(x)} = \sec^2(x)
$$

他

$$
\frac{d}{dx}\tan(xy) = \sec^2(xy) \cdot \frac{d}{dx}(xy)\\
= \sec^2(xy) \cdot (y + x\frac{dy}{dx})
$$

$$
\frac{d}{dx}\tan\left(\frac{1}{x}\right) = \sec^2\left(\frac{1}{x}\right) \cdot \frac{d}{dx}\left(\frac{1}{x}\right)\\
= \sec^2\left(\frac{1}{x}\right) \cdot (-\frac{1}{x^2})
$$

$$
\frac{d}{dx}\tan(\sqrt{x}) = \sec^2(\sqrt{x}) \cdot \frac{d}{dx}(\sqrt{x})\\
= \sec^2(\sqrt{x}) \cdot \frac{1}{2\sqrt{x}}
$$

ここで

$$
\sec(x) = \frac{1}{\cos(x)} \\
\sec^2(x) = \left(\frac{1}{\cos(x)}\right)^2 
$$

$${\frac{d}{dx} \tan(x) = \sec^2(x)}$$

$${\sec(\theta) = \frac{1}{\cos(\theta)}}$$

$${\frac{d}{dx} \frac{1}{\tan(x)} = \frac{d}{dx}\cot{x}}= -\csc^2(\theta)$$

$${\csc(\theta) = \frac{1}{\sin(\theta)}}$$

$${\frac{d}{d\theta} \left( \frac{a}{\tan(\theta)} \right) =-\frac{a}{\sin^2\theta}}$$

積の微分なら

$$
\frac{d}{d\theta} \left( \frac{a}{\tan(\theta)} \right) =0\cdot \frac{1}{\tan\theta}+a\cdot (\frac{1}{\tan\theta})'=a\cdot -\csc^2 \theta=a\cdot -\frac{1}{\sin^2 \theta}=\frac{-a}{\sin^2\theta}
$$

商の微分なら

$${\frac{d}{d\theta} \left( \frac{a}{\tan(\theta)} \right) = \frac{-a \cdot \sec^2(\theta)}{\tan^2(\theta)}=\frac{-a\frac{1}{\cos^2\theta}}{\frac{\sin^2\theta}{\cos^2\theta}}=\frac{-a}{\sin^2\theta}}$$

積の微分
$${(f(x) \cdot g(x))' = f'(x) \cdot g(x) + f(x) \cdot g'(x) }$$

商の微分
$${\frac{d}{dx}\left(\frac{f(x)}{g(x)}\right) = \frac{f'(x)g(x) - f(x)g'(x)}{g(x)^2}}$$

補助三角関数

$${ \cot, \sec, }$$および$${ \csc }$$は、それぞれコタンジェント、セカント、コセカントと呼ばれる三角関数です。これらはサイン、コサイン、タンジェントの逆関数として知られています。

$${ \cot(\theta) = \frac{1}{\tan(\theta)} }$$
コタンジェントはタンジェントの逆関数であり、タンジェントがオーバー1のとき、コタンジェントは1以下になります。タンジェントは0のとき、コタンジェントは無限大に近づきます。

$${ \sec(\theta) = \frac{1}{\cos(\theta)} }$$
セカントはコサインの逆関数です。コサインが1のとき、セカントも1です。コサインが0のとき、セカントは無限大に近づきます。

$${ \csc(\theta) = \frac{1}{\sin(\theta)} }$$
コセカントはサインの逆関数です。サインが1のとき、コセカントも1です。サインが0のとき、コセカントは無限大に近づきます。

これらの三角関数は、特に三角法や幾何学、計算などで使用されます。また、これらの関数は周期関数であり、定義域や値域に注意が必要です。それぞれの関数は特定の角度において未定義になることもあります（例：コセカントやセカントは$${ \theta = 0 }$$で未定義です）。

また、これらの関数を計算する際には、対応する基本三角関数の値を用いて計算することが一般的です。それぞれの関数には特定の性質や関連性があり、三角関数のアイデンティティ（同一性）や方程式を解く際に重要となります。

それぞれの三角関数の微分と積分を以下に示します。

微分

$$
 \frac{d}{d\theta} \cot(\theta) = -\csc^2(\theta) \\
 \frac{d}{d\theta} \sec(\theta) = \sec(\theta)\tan(\theta) \\
 \frac{d}{d\theta} \csc(\theta) = -\csc(\theta)\cot(\theta) 
$$

積分

$$
 \int \cot(\theta) , d\theta = \ln|\sin(\theta)| + C \\
 \int \sec(\theta) , d\theta = \ln|\sec(\theta) + \tan(\theta)| + C \\
 \int \csc(\theta) , d\theta = \ln|\csc(\theta) - \cot(\theta)| + C 
$$

逆関数

atan

$${ \arctan }$$はアークタンジェントまたは逆タンジェントと呼ばれ、タンジェント関数の逆関数です。記号としては$${ \tan^{-1} }$$とも表されることがあります。

定義:

$${ y = \arctan(x) }$$の場合、$${\tan(y) = x }$$です。また、アークタンジェント関数の定義域は全ての実数で、値域は$${-\frac{\pi}{2}から\frac{\pi}{2}}$$までです$${-\frac{\pi}{2} < \arctan(x) < \frac{\pi}{2}}$$。

性質:

1. 奇関数: $${ \arctan(-x) = -\arctan(x) }$$です。

2. 単調増加: $${ x_1 < x_2 }$$の場合、$${ \arctan(x_1) < \arctan(x_2) }$$です。

微分:

$${\arctan(x) }$$の導関数（微分）は以下のようになります。
$${ \frac{d}{dx}\arctan(x) = \frac{1}{1 + x^2} }$$

積分:

$${ \arctan(x) }$$の不定積分は以下のように表されます。
$${ \int \arctan(x) ,dx = x\arctan(x) - \frac{1}{2}\ln(1+x^2) + C }$$
ここで、C は積分定数です。

用途:

アークタンジェント関数は、特に三角法、幾何学、複素数、工学、物理学など多様な分野で用いられます。例えば、直角三角形の角度を求める際や、複素数を極座標形式に変換する際などに使用されます。

これらの基本的な性質や計算は、アークタンジェント関数を理解する上で非常に重要です。

acos

acos
入力は-1から1。
範囲外の入力にはNaNを返す。
出力は0からPI(3.1415927)

float val = acos(-2);//=>Nan
float val = acos(-1.1);//=>Nan
float val = acos(-1);//=>3.1415927
float val = acos(0);//=>1.5707964
float val = acos(1);//=>0