非圧縮性ナビエ・ストークス方程式

この記事はまだ勉強中です。

参考図書
流体解析の基礎 (日本語) 単行本 – 2014/3/26 河村 哲也 (著)
数値シミュレーション入門 (Computer Science Library) (日本語) 単行本 – 2006/7/1 河村 哲也 (著)
流体計算と差分法 (日本語) 単行本 – 2005/3/1 桑原 邦郎 (著), 河村 哲也 (著)
テンソル解析　基礎数学選書 23 田代 嘉宏 (著)

上の∇・v=0は連続の式。質量保存則。
下の式は非圧縮性ナビエストークス方程式。運動量保存則。この式は各種パラメータを無次元量に直してあるとのこと。
Reはレイノルズ数。無次元量化の影響を受け持つ係数。
流速が小さい、スケールが小さい、粘性が大きい＝レイノルズ数が小さい
慣性と粘性の比。レイノルズ数が小さい方が粘性が慣性に勝る。
レイノルズ数が小さい方が粘っこい。

ボールド体のニューは速度場、つまり出力に速度ベクトルを吐くベクトル場。pは圧力。2次の場合、速度場は

あるいは

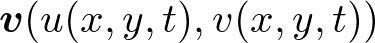
u,vは流体の速度成分。スカラー場。つまり出力にスカラーを吐く。
最初の式はu,vの成分毎の連立方程式を圧縮したもの。例えば２次の場合は以下のように表す。

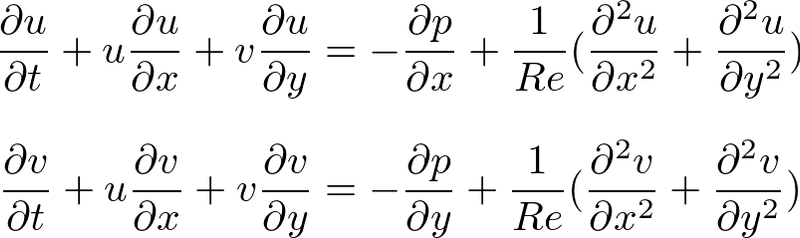
通常ベクトル場の発散なら出力はスカラー。テンソル場の発散なら出力はベクトル。出力にベクトル項を持つような式は、そのベクトルの次数に応じた連立方程式に分解されると考える。つまり出力が２次のベクトルなら形成される方程式は２つである。

発散

発散、イコールゼロなら連続の式を表す。

対流（移流）項：発散の逆のヤツ

発散に似てるが演算の方向が違うと発散ではない。出力はまだ演算子。どちらかといえばナブラの仲間である。
成分同士の積の総和をとると

$$
u\frac{\partial}{\partial x} + v\frac{\partial}{\partial y} 
$$

という形の演算子。

２次のナビエストークス方程式では以下のようにベクトル場を受け、各成分が連立方程式に振り分けられて登場する。

こっちはナブラ（横ベクトル）

スカラー場を受けると

ラプラシアン

次にラプラシアン（演算子）にベクトル場を引っ掛けたもの。スカラー場に作用すると出力はスカラー、ベクトル場に作用すると出力はベクトル。2次の場合

差分近似

ここで、これまで登場した中の1階偏微分と2階偏微分が差分近似の対象となる。

渦度・流れ関数法

圧力項を消去することを考える。

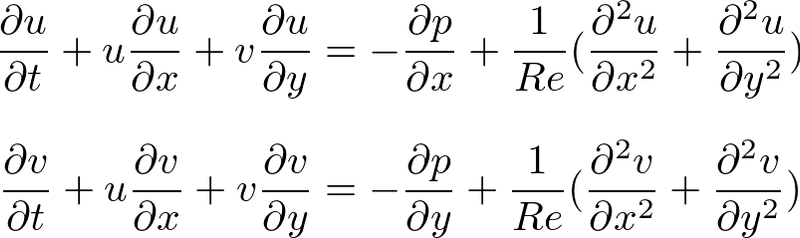
上の式をyで微分、下の式をxで微分、下の式から上の式を引く。

なる渦度関数を考慮すると

が導かれる。また、連続の式から

なる流れ関数の存在が定義できる。

全部あわせると

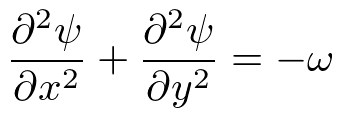
まだ途中。

MAC法の場合

圧力項を独立に求めることを考える。

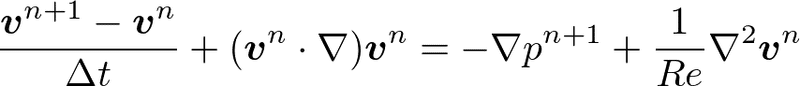
変形して

ここでnは時間ステップ。すなわちn+1付きの項は未知。
求めたいのはv^n+1であるが、v^n+1を求めるためにはp^n+1を求めることが必要。
そのためにはまず両辺の発散をとる

基本的にニューの発散は０であることを利用しながらn+1ステップのニューを消す。発散が含まれてる項は消そうと思えば消せるが、発散の逆のヤツは消えない。pに付いて解くと

nステップのニュー（右辺第一項）を残すのは誤差を吸収するためとのこと
ただし右辺三項は消しても問題ない。逆に言えば一項も三項も消すと誤差が発生する。二項は発散の逆のやつなので発散と違って消えない。この式は圧力に関するポアソン方程式に相当する。

つまり右辺はまとめてq(x,y)あるいはq(x,y,t)

これで圧力pに関してヤコビ法、ガウス・ザイデル法、ＳＯＲ法などの反復法で解くが、実際にナビエストークス方程式ではナブラが付いていることに注意。即ち実際に使う時には解いたｐ（２次元なら２重配列）の１階差分をとることとなる。

∇・(V・∇)Vは発散の逆のやつ（演算子）とベクトルの積＝ベクトルのさらに発散であるので、出力はスカラー。以下、下付き文字はその成分に関する偏微分を表す。

積の微分は

(u_x+v_y)は発散＝ゼロの部分、全部消える。

これで圧力項ｐは求まる。

ここまででてきたものを

に放り込む。するとＭＡＣ法の基本的な要素は完成であるが（あとは格子をズラしたり色々する）、今のところ数値が爆散してしゃーないのでコードの掲載は控える。