はじめに: ディジタル回路とアナログ回路
Johannes Kepler University Linz の Prof. Pretl による "Fifty Nifty Variations of Two-Transistor Circuits: A tribute to the versatility of MOSFETs" をテキストに,オープンソースの PDK である SkyWater 130 nm (sky130) を用いて回路設計を学んでいきます.ただ回路を動かすだけではなく,きちんと目的をもって「回路設計」を行いますので,ある程度理論的なことを理解しておく必要があります."Fifty Nifty" にはディジタル回路もアナログ回路も含まれており,また回路図は同じでもディジタル的な動作もアナログ的な動作もできる回路もあります.まずはディジタル回路とアナログ回路の違い,特に一般に「難しい」と思われているアナログ回路の考え方について説明します.
1.ディジタル回路とアナログ回路
1.1 ディタル信号とトランジスタの役割
ディジタル (digital) という単語は一般的には2進数,0と1で表された世界を指します.(厳密には必ずしも2進数でなくてもよいのですが.) 電気回路ではこの 0 / 1 を電圧の低 (LO) / 高 (HI) や電流の流れない/流れるに対応させてディジタル信号を扱う回路を構成します.つまり,ディジタル回路を構成するために必要なものは「スイッチ」です.出力ノードをLO もしくは HI に「つなぐ/つながない」,電流の経路を「開く/閉じる」をやればよく,LO と HI の中間の電位になったり電流がちょっとだけ流れたりされても困るので,きっぱりと開閉のどちらかの状態にしかならないスイッチが必要です.詳しい話は以下の記事を参照してください.
1.2 アナログ信号とトランジスタの役割
アナログ信号はディジタル信号と違い,波形 (振幅・周波数・位相) が情報を担っています.ディジタル回路 (ここでは同期式順序回路に限定します) では「ある一定のタイミング (クロック信号のタインミング) で 0 か 1 が判別できさえすれば波形は乱れていてもかまわない」という性質があります.下図のように様々な波形も,クロック信号のタイミングで 0 / 1 を判定するしきい値 (論理しきい値) より上か下かによって 0 か 1 かが決まります.つまり波形の乱れは情報の欠落を起こしません.(もちろん限度はあります.クロックのタイミングをまたぐような波形のずれや論理しきい値を超えるようなノイズは 0 / 1 の誤判定を起こします.)

これに対してアナログ信号は波形の「歪み」はすべてノイズとなります.ところで波形の「歪み」とは何でしょうか.波形をまったく変えてはならない,というのであれば波形の増幅も許されないことになります.波形のどのような操作であれば許されるのでしょうか.
アナログ変調を例に考えます.アナログ変調で情報を担う情報は,振幅 (AM: Amplitude Modulation),周波数 (FM: Frequency Modulation),位相 (PM: Phase Modulation) の3つです.数式で書くと
$$
s(t) = A\sin\left(\omega t + p\right)
$$
で,振幅 $${A}$$,周波数 $${\omega}$$,位相 $${p}$$ が情報を担っています.これらの情報を乱さない操作はどのようなものかというと,線形変換です.つまり
$$
f(t) = G\times s(t) + H
$$
ならば OK ということです.もし非線形な変換,例えば
$$
f(t)=s(t)^2
$$
をするとどうなるでしょう.三角関数の倍角公式より
$$
s(t)^2 = A^2\sin^2\left(\omega t + p\right) = \frac{1}{2} - \frac{1}{2}\cos\left(2\left(\omega t + p\right)\right)
$$
ですので,周波数が変わってしまいます.つまり,情報が変わってしまいます.逆に言うと,波形に情報を「追加」するためには非線形操作が必要ということです.詳しくは変調回路などを調べてください.変調回路は情報を持たない搬送波に情報を「追加」する回路です.
前置きが長くなりましたが,アナログ回路 (線形増幅回路) に求められるのは,「信号を線形変換する」ことだということです.ところがトランジスタは非線形素子です.さて,どうしたものでしょうか.
2.アナログ信号の分解: バイアス成分と信号成分
トランジスタは非線形素子ですが,ある程度の限定条件をつければ線形素子と見なすことができます.まず,信号波形 $${s(t)}$$ はフーリエ級数展開により
$$
s(t)=\frac{a_0}{2} + \Sigma_{k=1}^\infty\left(a_k\cos kt + b_k\sin kt\right)
$$
つまり時間 $${t}$$ に依存しない直流成分 $${a_0/2}$$ と正弦波の集まりに分解することができます.$${k\geq 2}$$ の高調波成分を考えるのは面倒なので,
$$
s(t)=V_{\text{b}} + V_0\sin\left(\omega t\right)
$$
のように,直流成分 (時間的に変動しない成分) + 正弦波成分 (時間的に変動する成分) で書くことにしましょう.この直流成分をバイアス成分 (bias voltage),時間的に変動する成分を信号成分と呼ぶことにします.バイアス成分の電圧をバイアス電圧,電流をバイアス電流と呼びます.また,動作点 (operating point) とほぼ等価です.
トランジスタの非線形性はとりあえず置いておいて,バイアス成分と信号成分の満たすべき条件について考えましょう.基本的に回路というものはグラウンド電位よりも低い電位や電源電圧よりも高い電位を出すことは簡単ではありません (出そうと思えば出せますが).
バイアス電圧については,電源電圧 VDD とグラウンド VSS の中間,中央付近にあることが望ましいと言えます.下図のように,バイアス電圧が電源電圧やグラウンド電位に近いと,波形が削られる (クランプされる) ことで歪んでしまいます.よってバイアス成分は「VDD と VSSの 中間のいい感じのところ」であって欲しいということです.

では信号成分はどうでしょう.ひとまずバイアスは「いい感じ」ということで VDD/2 付近にあるものとします.このとき信号成分は「信号は VDD or VSS に到達することがない程度に小さい振幅である」ことが求められます.下図のように,いくらバイアスが VDD/2 付近にあったとしても,信号成分の振幅を大きくしていけば VDD and/or VSS によるクランプは発生します.

実際には信号電圧が VDD / VSS に達しなくても波形は歪みますので,信号成分は「波形が歪まないようにじゅうぶんに小さい振幅であること」が望ましい条件ということになります.
まとめると,アナログ信号は「バイアス成分はいい感じの電位にあり,信号成分の振幅はじゅうぶんに小さい」ことが線形増幅をするために求められる,ということです.
3.小信号と微分特性
さて,前節の「じゅうぶんに小さい振幅」とはどの程度の振幅でしょうか.また,振幅がじゅうぶんに小さいとき,トランジスタはどのように扱えるでしょうか.その答えがアナログ回路を考える根幹とも言える小信号解析 (small-sginal analysis) です.
3.1 線形で解きたい
なぜここまで線形 (linear) にこだわるのか.線形であれば波形が歪まないというのもその理由の一つですが,線形の問題を解くのと非線形の問題を解くのでは難易度が圧倒的に違うからです.もちろん線形の方が簡単です.線形性 (linearity) は以下の性質をもつことです
$$
f(x + y) = f(x) + f(y) \hspace{16pt} (\text{加法性 additivity}) \\
f(a\cdot x) = a\cdot f(x) \hspace{16pt} (\text{斉次性 homogeneity})
$$
加法性は,「和 $${x+y}$$ に $${f}$$ を作用させた結果は,$${x}$$,$${y}$$ それぞれに $${f}$$ を作用させた結果の和をとったものに等しい」ということで,斉次性は「係数 $${a}$$ を掛けたものに $${f}$$ を作用させた結果は,$${f}$$ を作用させてから係数 $${a}$$ を掛けた結果に等しい (係数 $${a}$$ と作用 $${f}$$ は可換である)」ということです.つまり,変数 $${x}$$ が線形結合 $${a_0x_0 + a_1x_1 + a_2x_2 +\cdots}$$ で表されるなら,各成分 $${x_0}$$,$${x_1}$$,$${x_2}$$・・・について解いてから後で線形結合すればよいということです.これは非常に強力です.複雑な波形もフーリエ級数展開すれば,正弦波の線形結合
$$
s(t)=\frac{a_0}{2} + \Sigma_{k=1}^\infty\left(a_k\cos kt + b_k\sin kt\right)
$$
で表されるわけですから,線形系であれば正弦波に対する応答 (と直流成分に対する応答) を集めてくればよいということになります.
また,信号源が複数ある場合であっても1つずつ解いて後で足し合わせればよいことになります (重ね合わせの理 superposition theorem).
さらに,線形回路であればあるポートから見たときの振る舞いは内部抵抗をもつ等価電源 (もしくは電流源) によって表すことができる,というテブナンの定理 (Thévenin's theorem) / ノートンの定理 (Norton's theorem) も使うことができます.
以上のように,線形回路に対しては非常に強力な定理を使うことができるため, 解析の簡単さは段違いです.なので,できれば線形問題を解きたい.というか非線形問題は解きたくない.トランジスタは非線形素子ですが,なんとかならないものでしょうか.
3.2 非線形デバイスの線形近似
MOSトランジスタの電圧と電流の関係は非線形です.詳しくは別の記事でやりますが,例えばゲート-ソース間電圧 $${V_{\text{GS}}}$$ とドレイン電流$${I_{\text{D}}}$$ の間の関係は下図のように曲線になります.電圧と電流が線形の関係 ($${I=A\times V + B}$$ であればグラフは直線になるはずです.グラフが曲線なのは非線形ということです.

しかしこの曲線,曲がっているのは電流が増え始めるところだけで,あとはほぼ直線で構成されています.この特性は本当にまじめに非線形として解かなければならないのでしょうか? ここでアナログ信号の性質を思い出すと,アナログ信号は「バイアス成分の周辺 + 小さい振幅の信号」で構成されています.下図のように,バイアス点の周辺で信号の振幅が小さく,信号が動く範囲内に限って言えば直線だと思って問題ないのであれば,トランジスタは赤線のような線形の特性をもっていると見なしてもよいはずです.
もちろんバイアス点から離れていくと本来の特性である青線と線形近似である赤線は大きく乖離していきます (特にVGS が小さい領域) が,そんなことはどうでもいいのです.信号はバイアス点のまわりでしか動かないのですから.

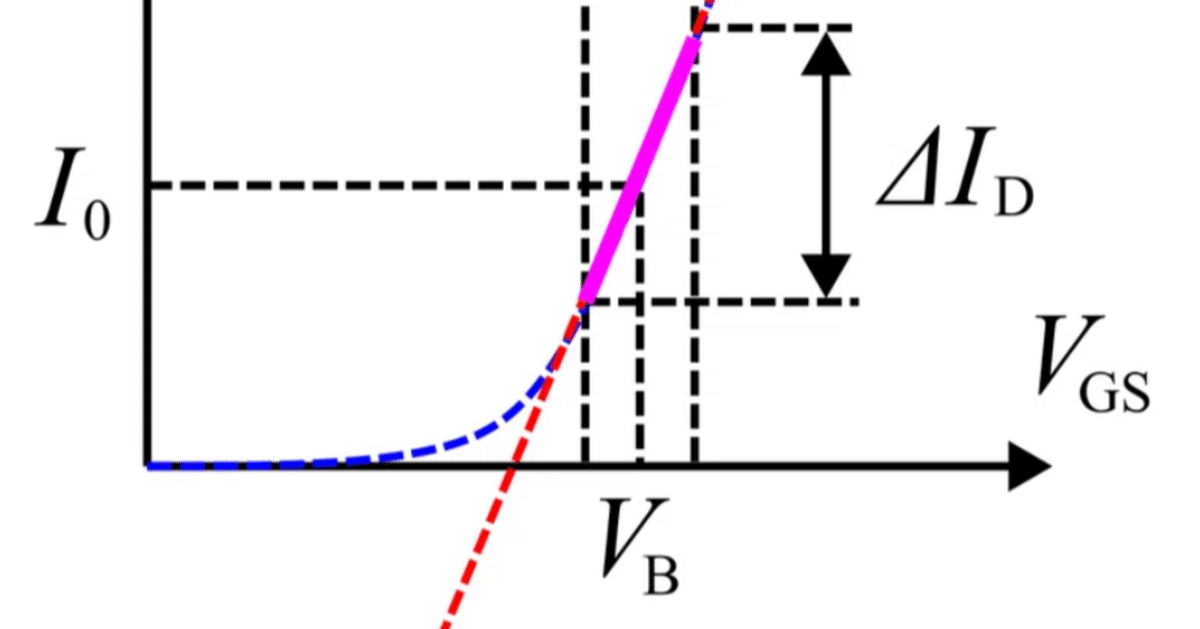
ではこの線形近似の直線がどういうものか考えていきます.下図のように,バイアス電圧を $${V_{\text{B}}}$$,そのときの電流を $${I_{0}}$$ とします.信号成分の動く範囲を $${\Delta V_{\text{GS}}}$$,$${\Delta I_{\text{D}}}$$ とすると,直線の傾きは $${\Delta I_{\text{D}}/\Delta V_{\text{GS}}}$$ です.これは信号成分を無限に小さくしていくと,$${V_{\text{B}}}$$ における接線の傾き $${\partial I_{\text{D}}/\partial V_{\text{GS}}}$$ となります.これを $${g_{\text{m}}}$$ と書くことにします.傾きが $${g_{\text{m}}}$$ で $${\left(V_{\text{B}}, I_0\right)}$$ を通る直線ですから,線形近似した赤線の方程式は,$${I_{\text{D}} - I_0 = g_{\text{m}}(V_{\text{GS}} - V_{\text{B}})}$$ となります.

と,ここまで書いておいて何ですが,$${I_{\text{D}} - I_0 = g_{\text{m}}(V_{\text{GS}} - V_{\text{B}})}$$ を考える必要はありません.なぜなら線形近似によってこの問題は線形系にもちこまれましたので,バイアス成分と信号成分は分離して解けばよいのです.$${I_{\text{D}}}$$ の信号成分を $${i_{\text{d}}}$$,$${V_{\text{GS}}}$$ の信号成分を $${v_{\text{gs}}}$$ と書くことにすると,
$$
i_{\text{d}} = g_{\text{m}}v_{\text{gs}}
$$
を解けば信号の振る舞いは分かります.このように,バイアス点で線形近似して信号成分をバイアスと分離して解くことを小信号解析と呼びます.慣例として,小信号成分は小文字で書きます.(上のように添字まで小文字にするかどうかは人によるような気もしますが,私は添字も小文字にする方です.)
ここで注意しなければならないのは,この小文字で書いた電圧や電流はバイアス点を中心とした変動成分のみであるということです.そのため,電圧源や電流源のように変動しない電圧/電流は小信号解析では0になります.つまり電圧源はグラウンド (0 V),電流源は開放として扱わなければならないということです.これは実際に小信号解析を行なう際に詳しく説明します.
3.3 小信号等価回路
では,小信号解析をする際にトランジスタはどのように扱えばよいでしょうか.線形近似されていますので,線形素子による等価回路に変換することができます.このときの等価回路が小信号等価回路 (small-signal equivalent circuit) です.
とは言ってもトランジスタは少なくとも3つ端子があるし,なんか複雑そうな構造だし… と思うかも知れませんが,小信号の解析では線形近似をしています.線形回路ということは,テブナンの定理が使えるということです.
電源 (電圧源・電流源) および抵抗からなる線形回路は,あるポート (2端子) から見たとき,1つの電圧源と1つの抵抗 (テブナンの等価電圧源) で表すことができる.
「ポートから回路を見る」は電気回路の方言のようなもので,「ある2端子の端子間電圧と端子に流れ込む電流の関係を調べる」という意味です.また,双対形として,1つの電流源と1つの抵抗 (ノートンの等価電流源) で表せることを示したのがノートンの定理 (Norton's theorem) です.

実はヘルムホルツが先 (1853年.テブナンは1883年)に発表していたためヘルムホルツ-テブナンの定理と呼ぶとか,交流信号で成立することを示した鳳にちなんで鳳-テブナンの定理と呼ぶとかいろいろ呼び方はありますが,呼び分けるのは面倒なのでこの記事ではノートンの定理および交流信号への拡張もすべてひっくるめて「テブナンの定理」と呼ぶことにします.
テブナンの定理により,どんなに複雑な回路であっても中身はブラックボックスとして等価回路にしてしまってよいということです.ドレイン・ゲート・ソースの3端子のトランジスタは下図のような2端子対網となるので,2つの等価電源で表すことができます.つまり,多くとも4つのパラメータがあればその特性を記述できるということです.図ではゲート-ソース端子から見た方を電圧源,ドレイン-ソース端子から見た方を電流源で書いていますが,これはもちろん電圧源/電流源どのような組み合わせでも書くことができます.

4.まとめ
アナログ回路を理解する上で必須となるバイアスと信号成分の分離,およびその背景にある線形近似について解説しました.この部分は実際に自分で回路を解析しようとすると,多くの人が頭を悩ませる箇所です.小信号等価回路で具体的に回路を解いていく段になって混乱した場合はこの内容を読み返してください.
この記事は Fifty Nifty Variations of Two-Transistor Circuits の解説記事の一つです.
この記事が気に入ったらサポートをしてみませんか?
